
Cinderella で数学・情報:基数変換
基数変換について,Cinderella を利用して学びます。CindyScript を使ったプログラミングの練習にもなります。
2進法と16進法
コンピュータは2進法で計算を行います。2進法で表された数の1桁のことを ビット(bit)といいます。コンピュータでは、4bit、8bit、16bit・・ という単位で数を処理します。その場合、上位桁が0の場合も「0」を書いて、常に0か1を4個、8個、16個、・・・と書くのが普通です。
たとえば,4bit の2進法で表された数は $${0000_{(2)}}$$ から $${1111_{(2)}}$$ まで,8bitの2進法で表された数は $${00000000_{(2)}}$$ から,$${11111111_{(2)}}$$ までです。
なお,n進法で表された数は、右下に (n) と表記します。(10進法で表された数の場合は略す。)
コンピュータは2進法で計算をしますが、コンピュータを扱う人間は16進法で表された数を用います。16だけ進むと桁が上がる位取り記数法が16進法です。16進法で表された数では15まで桁が上がらないので、0〜9の数字と、アルファベットA〜Fを用いて数を表します。これは,2進法の表記とうまく対応しています。
たとえば,4bit の2進法で表された$${0000_{(2)}}$$ から $${1111_{(2)}}$$までの数は,16進法では $${0}$$ から $${F_{(16)}}$$ まで,8bitの2進法で表された $${00000000_{(2)}}$$ から,$${11111111_{(2)}}$$ までは $${00_{(16) }}$$から $${FF_{(16)}}$$ までです。
位取り記数法と基数変換
私たちが通常扱っている整数は、10進法で表されています。「10まで進んだら桁が上がる」というものです。このような「桁」によって数を表す方法を「位取り記数法」といいます。一般に、nだけ進むと桁が上がる位取り記数法をn進法といいます。
m進法で表された数をn進法に変換することを基数変換といいます。10進法と2進法の変換は数学や情報の教科書に載っていますが,きちんと理解するには位取り記数法の理解が必要です。
たとえば,次のようにします。
$${4052=4 \times 10^3 + 0 \times 10^2 + 5 \times 10^1 + 2 \times 10^0}$$
$${1101_{(2)}=1 \times 2^3 + 1 \times 2^2 + 0 \times 2^1 + 1 \times 2^0}$$
この表記法を利用すると,n進法で表された数を10進法で表された数にするには,上のように指数を用いて和を求めればよく、逆に10進法で表された数をn進法で表された数に変換するには,nで割った余りをどんどん求めていけばよいことがわかります。
【例】1970 を16進法で表された数にする。
1970 を 16 で割ると商が 178 ,余りが 7。178 を 16 で割ると商が 11, 余りが2,11 は16進法で B なので,$${1970=7B2_{(16)}}$$
表計算ソフトには,10進法,2進法,16進法の換算を行う関数があります。たとえば,Excelの場合次のような関数があります。
DEC2BIN :10進法から2進法への変換。
DEC2HEX :10進法から16進法への変換。
BIN2DEC :2進法から10進法への変換。
HEX2DEC :16進法から10進法への変換。
しかし,あまり大きな数の換算はできません。
これらの変換をするプログラムをCindyScript で作ってみましょう。
10進法から2進法へ
10進法から2進法に変換する関数を作ります。
8ビット(1バイト)の2進法では、10進法の0から255まで(負でない整数の場合)まで表せます。16ビットでは0から65535までです。現在のコンピュータは64ビットでの計算が普通ですが、まずは16ビットくらいまでは変換できるようにしましょう。
10進法を2進法に変換するには、正の整数の場合、2で次々に割りながら、その余りをビットとして立てていくのでした。このことは、単に手続きとして暗記するのではなく、位取り記数法の原理として理解しておきましょう。これについては,「生徒が苦手な基数変換」という記事を書いています。
では、10進数を2進数に変換する関数を作ります。関数定義なのでInitializationスロットに書くとよいでしょう。
bin = ["0", "1"];
dec2bin(n):=(
keta = if(n > 255, 16, 8);
binstr = "";
repeat(keta,
binstr = bin_(mod(n, 2) + 1) + binstr;
n = floor(n/2);
);
binstr;
);1行目:2進数の各桁で使う文字、0と1をリストにしておきます。
2行目が関数の名前。引数はnです。ここで、nは正の整数であるという前提です。そうでない場合はどうするかはあとで考えましょう。
3行目、引数のnの大きさにより、8ビットで表すか16ビットで表すかを決めます。この数は、6行目の繰り返し数にもなります。
4行目、戻り値の文字列です。最初は空。
5行目から8行目が計算。繰り返しです。
6行目、nを2で割った余りを求めます。0か1ですので、1を足してbinリストから該当する文字を取り出します。たし算になっていますが、文字列のたし算は文字の追加になります。
7行目、nを2で割った商をあらためてnとします。floorという関数は床関数というもので、その数を超えない最大の整数を求めるものです。数学の教科書ではガウス記号で表されるものです。floorはCindyScriptに用意されている関数です。
途中でnは0になることがありますが、かまわず繰り返します。それによって8ビットもしくは16ビットの表示ができるわけです。
9行目、戻り値です。CindyScriptの関数定義では、最後に評価された(計算された)結果が戻り値となります。ここでは何も計算していませんが,binstrを「評価」したので、binstr が戻り値となります。この行がないと、戻り値は7行目のnになってしまいます。
これで関数定義ができたので、Drawスロットに書いて実行してみましょう。
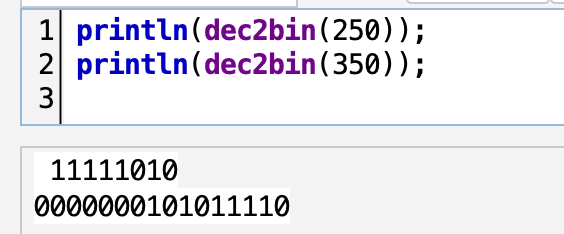
10進法から16進法へ
10進法を16進法に変換する関数を作ります。原理は2進法の場合と同じですから、先ほどのスクリプトを少し書き換えればいいですね。
最初に16進法で使う文字0からFまでのリストを作っておきます。16進法なのでこんどは hex とします。
hex=["0", "1", "2", "3", "4", "5", "6", "7", "8", "9", "A", "B", "C", "D", "E", "F"];
あとは、255以下なら2桁表示、256以上なら4桁表示とし、2で割るところを16で割るようにすればいいだけです。実際のコードは読者の課題としましょう。
こんな結果になります。
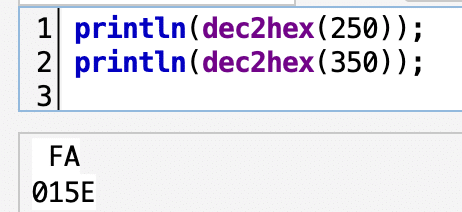
2進法から10進法へ
2進法の数も16進法の数も,プログラム上では文字列として扱わなければなりません。そこで,引数も文字列として渡します。
2進法なら右から1ビットずつとって数に変換し,2のn乗(nは桁数)をかけて足していけばいいのです。数に変換するには,parse という組み込み関数があります。
bin2dec(str):=(
ret = 0;
repeat(length(str), n,
bit = str_(-n);
ret = ret + parse(bit)*2^(n-1);
);
ret;
);dectbin で2進法にした数を,これで戻してみましょう。
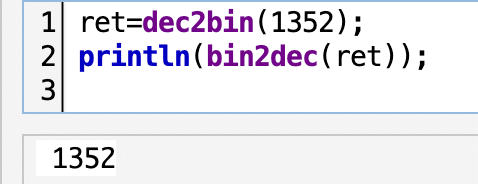
16進法から10進法へ
これも,左から1文字ずつとって10進数にし,16のn乗(nは桁数)をかけて足していけばいいでしょう。16進法の文字は,文字列 "0123456789ABCDEF" の何文字目かを取得すれば10進法の数になります。
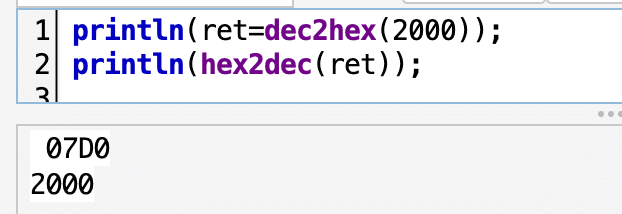
hex2dec(str):=(
ret = 0;
repeat(length(str), n,
w = str_(-n);
m = indexof("0123456789ABCDEF",w);
ret = ret + (m-1)*16^(n-1);
);
ret;
);
負の数へ拡張
ExcelやCalcのDEC2HEX関数は、負の整数も変換します。−512までです。つまり、ExcelやCalcでは、2進法への変換については、10ビットまでできるということになります。ただ、プログラミングの観点からすると、10ビットというのは中途半端なので、ここでも8ビットまたは16ビットとしましょう。
さて、8ビットで正の数と負の数を表すためには、まず、「正か負か」という情報が必要になり、そのために最上位(一番左)の1ビットを使います。ここが0なら正、1なら負、とします。残り7ビットで数を表すので、正の数は127まで表せます。次に負の数ですが、「絶対値が同じ正の数と負の数の和は0」ということに着目します。さらに、2進法では、1+1=10 と「1たす1」で桁が上がって0になる、ことも考慮すると
0001+1111=10000
となって、はみだした一番左の1を除けば4ビット分は0になります。すなわち、−1を4ビットで表すと1111です。このような表現方法を「2の補数」というのですが、この「補数」というのがわかりにくい言葉で、これでめげてしまう人も結構います。教科書によっては「各ビットを反転させた1の補数に1を加える」という説明がしてあるのもあり、「補数」でますますわけがわからなくなる人もいるでしょう。
「補数」はパスして、「1111(8ビットなら11111111)が −1でそこから1ずつ引いていく(−2は1110、−3は1101・・・)」と考えたり、「とにかく足して 0000・・・になるようにする」と考えたり、そこは人によって覚えやすい方法をとればよいでしょう。
では、スクリプトを書くには、どのアルゴリズムを使えばよいでしょう。
「各ビットを反転させた1の補数に1を加える」の「1を加える」がヒントになります。実際の表記を眺めてみましょう。簡単のため4ビットにします。
10進法 −5 −4 −3 −2 −1 0 1 2 3 4 5
2進法 1011 1100 1101 1110 1111 0000 0001 0010 0011 0100 0101
たとえば,「−4に1を加えて−3。符号を変えた3のビットを反転させれば−4の2進表記」になっています。「−4の符号を変えて4,1を引いて3,3のビットを反転」でもいいでしょう。
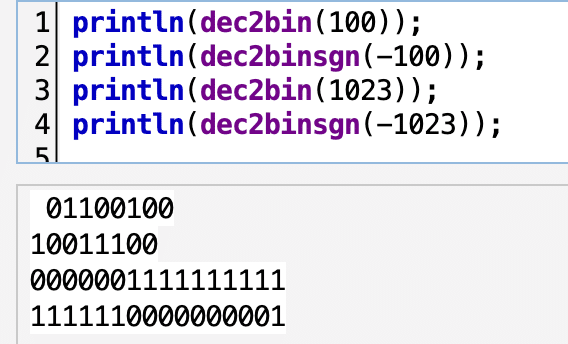
次のようなスクリプトにしてみました。関数名は、符号付ということでsgnをつけました。
dec2binsgn(n):=(
regional(bin);
keta = if(or(n>127, n<-128), 16, 8);
if(n < 0,
bin = reverse(bin);
wn = abs(n) - 1;
,
wn = n;
);
binstr = "";
repeat(keta,
binstr = bin_(mod(wn, 2) + 1) + binstr;
wn = floor(wn/2);
);
binstr;
);2行目:bin をこの関数の中だけで使う局所変数にします。というのは,5行目でbin を書き換えてしまうからです。こうすれば,この関数を呼び出すたびに,bin が定義されます。
4,5行目: nが負の数だったら、binの順序を入れ替えて bin=["1","0"] にするのです。つまりビット反転。
6行目: wnを設定します。「nの符号を変えて1を引く」
8行目 :nが負でなければ、wnはそのままnを代入します。
10行目から後は dec2bin と同じ。次々に2で割っていきます。
小数の変換
まず、小数の表記を分数表記で見てみましょう。
10進法では次のようになっています。
$${0.1 = \frac{1}{10}}$$ , $${0.01 = \frac{1}{10^2}}$$ , $${0.001 = \frac{1}{10^3}}$$ ・・・・
2進法では
$${0.1 _{(2)}= \frac{1}{2}}$$ , $${0.01_{(2)} = \frac{1}{2^2}}$$ , $${0.001_{(2)} = \frac{1}{2^3}}$$ ・・・・
たとえば、 0.8125 を2進法で表すと
$${0.8125=0.5+0.25+0.0625=\frac{1}{2}+\frac{1}{2}^2+\frac{1}{2}^4}$$
なので $${ 0.1101_{(2)}}$$ となります。
したがって,次々に2をかけながら、その整数部分をとっていけばよいことになります。ただし、整数の場合と違って、いつまでたっても終わらないことがあります。無限小数になるのです。そこで、どこかで打ち切ることにしますが、16ビットまでいったら打ち切ることにしましょう。そのためには、repeat文での繰り返しではなくwhile文での繰り返しを行ないます。整数の場合と違って少し複雑です。
decimal2bin(x):=(
regional(bin);
bin = ["0","1"];
if(x >= 1,
binstr = "換算する数は1未満の小数です";
,
binstr="0.";
keta =0;
while(and(x != 0, keta < 16),
wx = x*2;
binstr = binstr + bin_(floor(wx) + 1);
x = wx - floor(wx);
keta = keta + 1;
);
if(and(keta == 16, x != 0),
binstr = binstr + "・・以下さらに続きます";
);
);
binstr;
);4行目: 1より小さい小数の変換をする関数ですので1以上の場合はここでエラーメッセージを出すようにします。
7行目から xが1未満であればここからあとが実行されます。binstrは小数なのでまず "0." にします。
8行目: 整数の場合と異なり、桁数ははじめに決めるのではなく、カウントをしていきます。はじめは0にしておきます。
9行目 while(A,B) はAが成り立つ間Bを実行する、という繰り返し構文です。and(C,D)は、CかつDです。終了するのは、2倍していって整数部分を取り除き、最後に0になったときです。ですから、xが0でない(!=0)あいだ繰り返します。もうひとつ、桁数が16桁未満なら繰り返します。この2つの条件が両方とも成り立つときなので、and です。
10行目: xに2をかけたものをwxとします。
11行目:2をかけた wxが1より大きくなったら1を、そうでなければ0を取り出すために、床関数 floor を使います。floor(wx) は0か1なので、0ならば、bin=["0","1"]の1番目、1ならば2番目を取り出して、binstrの右に付け加えます。
12行目 wxから0か1を引いてあらためてxとします。
13行目 何桁作ったかカウントします。
16行目 :16桁までやって終わらない場合、「さらに続きます」という文字を付け加えます。
次が実行結果です。
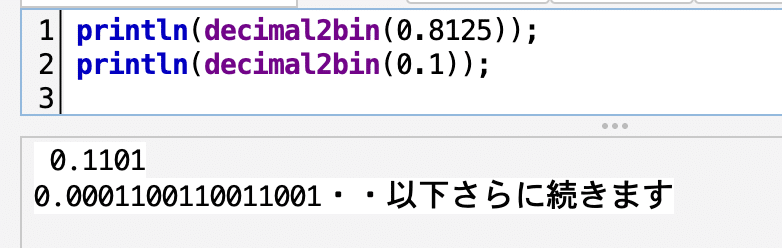
0.1 は2進法では無限小数になるのです。
浮動小数点数
実数は、浮動小数点という方法で表します。
10進法で表された数で大きな数や微小な数を表すとき、次のように指数を使って表す方法があります。
【例】地球の体積 およそ $${1.0833207 \times 10^{12} km^3}$$ (1兆833億・・・)
水素原子の原子核の大きさ およそ $${1.0 \times 10^{-15} m}$$
これと同様に、2進法で表された数でも指数を使って実数を表すことができます。
【例】10進法で表された数 150.8125 を2進法で表された数で表すと,
$${10010110.1101}$$ となる。
小数点を7つ左にずらすと
$${1.00101101101 \times 2^7}$$
この数は、小数点以下の 00101101101 と 指数 7 (2進法で表すと 0111) で
表現できる。
00101101101 を仮数部、 0111 を指数部といい、これに正負の符号を表す1ビットを加えて、次のように表します。(実際の指数部は指数7に127を加えた 134 を2進法で表された数にします)
0 10000110 00101101101000000000000
符号部 指数部(8bit) 仮数部(23bit 左から埋めて右方は0にする)
これは、32ビットで実数を表す単精度浮動小数点数です。さらに64ビットを用いて精度の高い数を表す倍精度浮動小数点数もあります。
プログラムについては,読者の課題としましょう。
基数変換ツール
,10進法,2進法,16進法の相互変換をする「基数変換」をWeb上で実行できるページを作りました。いままでに作った関数の確かめとしても使えるでしょう。
リンク先を開くと次の画面になります。
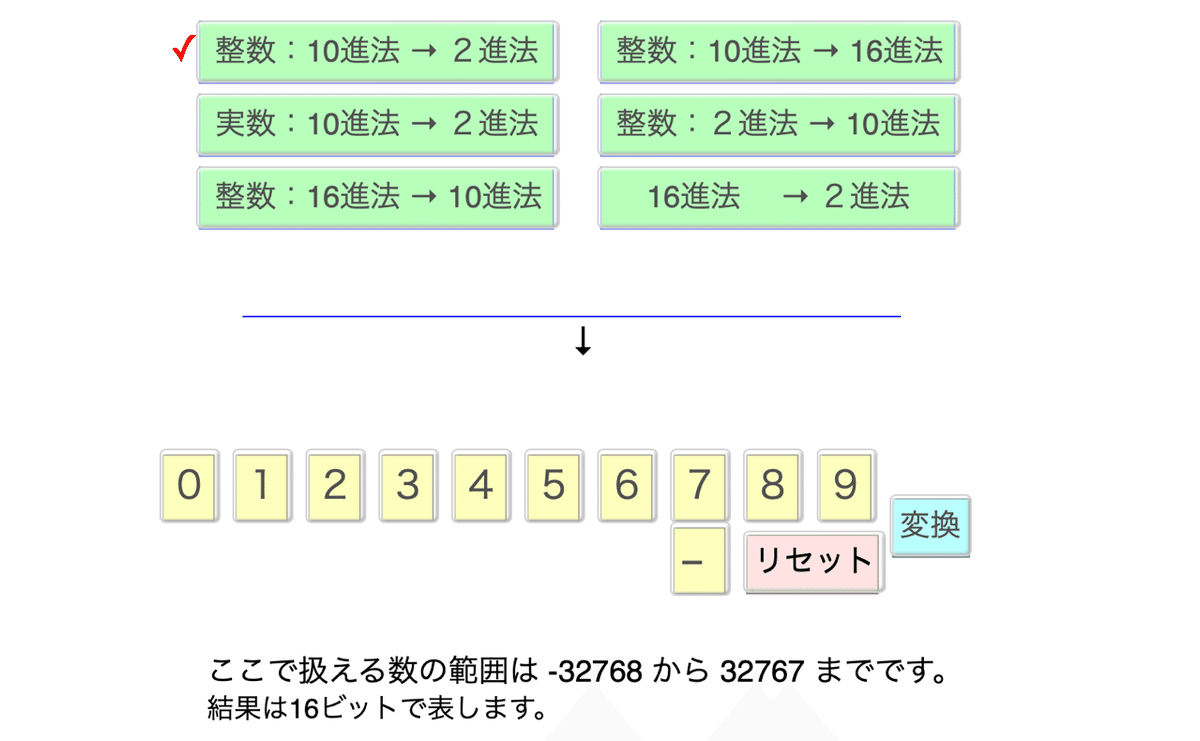
実数10進法→2進法 の実行例がタイトル画像です。
← Cinderellaで数学・情報記事一覧に戻る
