Cinderellaで花を描く:花びら(1) :正葉曲線
正葉曲線
はなびらを表現するのに基本になるのが正葉曲線です。バラ曲線ともいいます。正葉曲線を表す式は、極座標における極方程式 r=sin(nθ) が基本ですが、nを分数にして
$${r=\sin \frac{n \theta}{k}}$$
の形にします。$${n}$$と$${k}$$の値によってさまざまな図ができます。次の表は$${n, k}$$が1から5までの組み合わせです。

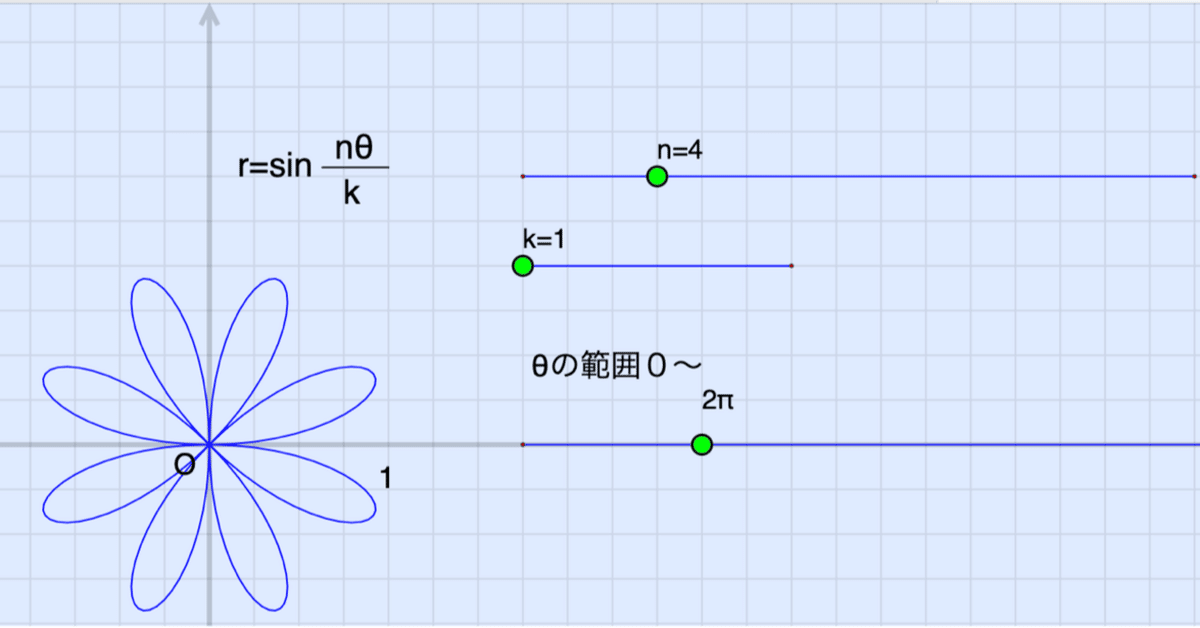
k=1の場合は、θは0から2πまでの範囲で描けますが、kの値が2以上になるとθの範囲を広げる必要がでてきます。
これらをシミュレートするものを作ってみましょう。次のような画面構成です。

3つのスライダーを作って、n,kの値と描画範囲を設定できるようにします。(スライダの作り方を参照のこと)
n,kは整数にしますので、スライダの左端の点がF,線分上の点がCのとき,床関数 floor を使って
k=floor((F.x-C.x)*4+0.1)+1;
のようにします。0.1は誤差を吸収するためのものです。磁石ツールをONにしておくと、方眼の交点のところでちょうど吸い付くようにマッチするようになりますが、このとき誤差のために整数にならないことがあるためです。
nとθも同様にしてスライダで取得するようにします。
実際の描画はデカルト座標系なので
r(t):=sin(n*t/k);
fx(t):=r(t)*cos(t);
fy(t):=r(t)*sin(t);
として、fxとfyの媒介変数表示にして描きます。媒介変数なので、plot関数を用いて次のようにすればよいのです。
plot([fx(#), fy(#)], start -> 0, stop -> th*pi, steps -> 200);
thはスライダで設定した値です。また,steps の値によって曲線をなめらかに描くことができます。
これをWeb上で動くようにしたものが次のページにあります。
ところで、極方程式 r=sin(nθ) で表される曲線は、nが偶数のときは2n枚の葉、nが奇数のときはn枚の葉が描かれますね。なぜこの違いができるのでしょうか。それは、上のシミュレータだけではちょっとわかりにくいでしょう。θの値の変化につれて、図がどのように描かれていくのかを理解しないとその理由はわかりません。次の節ではそのようなものを作って、正葉曲線について少しつっこんで考えてみましょう。
