
Cinderellaで数学:いろいろな曲線:スアルディの木の葉
「曲線の事典」(礒田正美他・共立出版2009)に掲載されている,スアルディの作図器による木の葉曲線を描きます。
平面に固定された点Oを通る円$${\gamma}$$が点Qを中心に回っている。点B,C,Dは円周上の点で同時に回転している。軸OBは点Oで固定されており、線分 CDはこの円の中心Qを通り、この円の直径となっている。
円$${\gamma}$$が回転するとき、OBとCDの交点Pは曲線をかく.これをスアルディの木の葉曲線という*3。直線0Qに関して対称な曲線である。

Web上では,次のページに作図器の写真と説明が載っています。
Cinderella による作図自体は難しくありません。円を描き,線分OBを描き,BとCが同時に動くようにBを中心とした円を描き,交点をCとします。中心QについてのCの鏡映を作り線分で結びます。次の図は作図後,上の図に合わせて点の名称を変えました。

軌跡ツールで,動かす点をB,軌跡を描く点をPとすると軌跡が描かれます。

円の外側にも軌跡が描かれていますが,実際に点Bをドラッグしていくと描くことができるのは円の内部だけだということがわかります。回転していって,点DがOを越えると交点Pはできません。
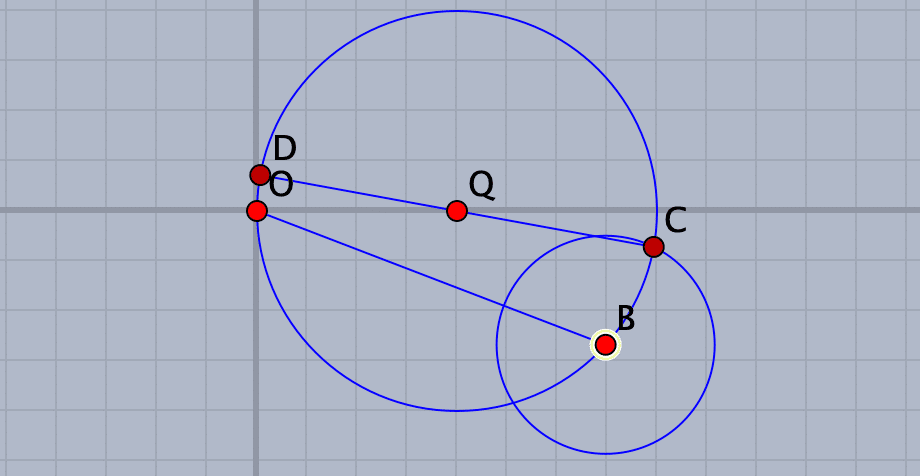

また,描かれるのは2枚の葉のうち一方だけです。BとCの位置関係を作図器の写真のようにしてみると,もう一方の葉が描かれます。
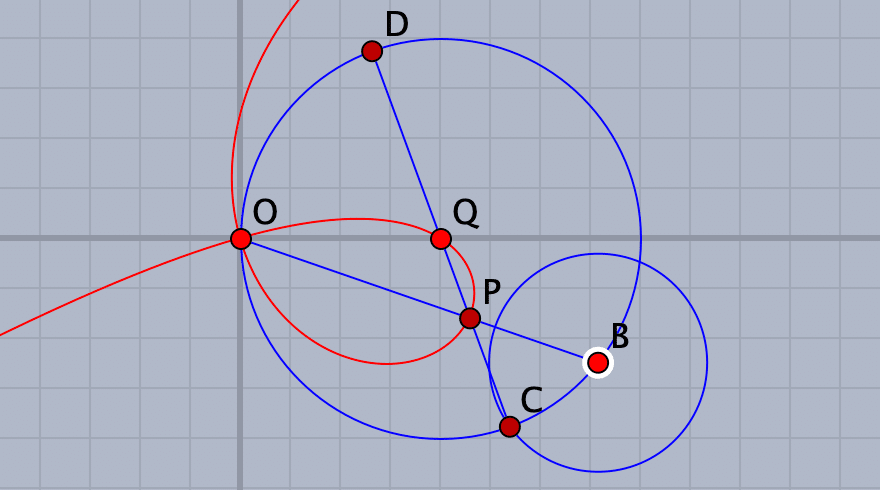
点CをBの両側に取れば2枚の葉が描かれますが,点Bの位置によっては1枚しか描かれません。

Bを中心とする円の半径を大きくして,OBとCDが垂直になるようにすると,ストロフォイドになります。

作図器で描くことができる図のように葉の描画を円の内部だけにするには,CindyScript で曲線を描きます。曲線の事典の解説では,極方程式で
$${r}$$=OQ,$${\alpha}$$=∠BQC,$${\theta}$$=∠QOP,$${\sigma}$$=OPとして
$${\sigma=\dfrac{r(\sin (\alpha+2\theta)}{\sin (\alpha+\theta)}}$$
としています。これで1枚の葉です。
作図器を模したものを作りました。
