Cinderella で数学:媒介変数と曲線・トロコイド
「円を含む円盤面が与えられており、円盤上の円が直線上を滑ることなく回転する。円盤上の点Pが円周上にあるときの軌跡をサイクロイド、円盤上に限らないときの点Pの軌跡をトロコイドという。特に、円盤の内にあるときを内トロコイド(ハイポトロコイド)、外にあるときを外トロコイド(エピトロコイド)という。」
「円が直線上をすべることなく回転するとき,円周上の1点が描く曲線」がサイクロイドで,高校の教科書にも載っています。サイクロイド曲線は媒介変数を使った方程式で表しますが,その他の媒介変数と曲線については,高校の教科書は軽い扱いになっています。リサージュ(リサジュー)やアステロイド,正葉曲線なども載っていますが,式の紹介くらいで,「コンピュータを利用してかいてみよう」というくらいです。そのため,授業で扱っているかというと,ほとんどやっていないでしょう。
円も媒介変数で表せますし,等速円運動を考えれば,座標は時間の関数になります。斜方投射でできる放物線もそうです。サイクロイドにしても,冒頭のトロコイドや,円周上のを回転するエピサイクロイド,ハイポサイクロイドなど,いろいろやってみると面白いのです。この節では,まずトロコイドを Cinderella で描いて楽しみましょう。
サイクロイドとトロコイド
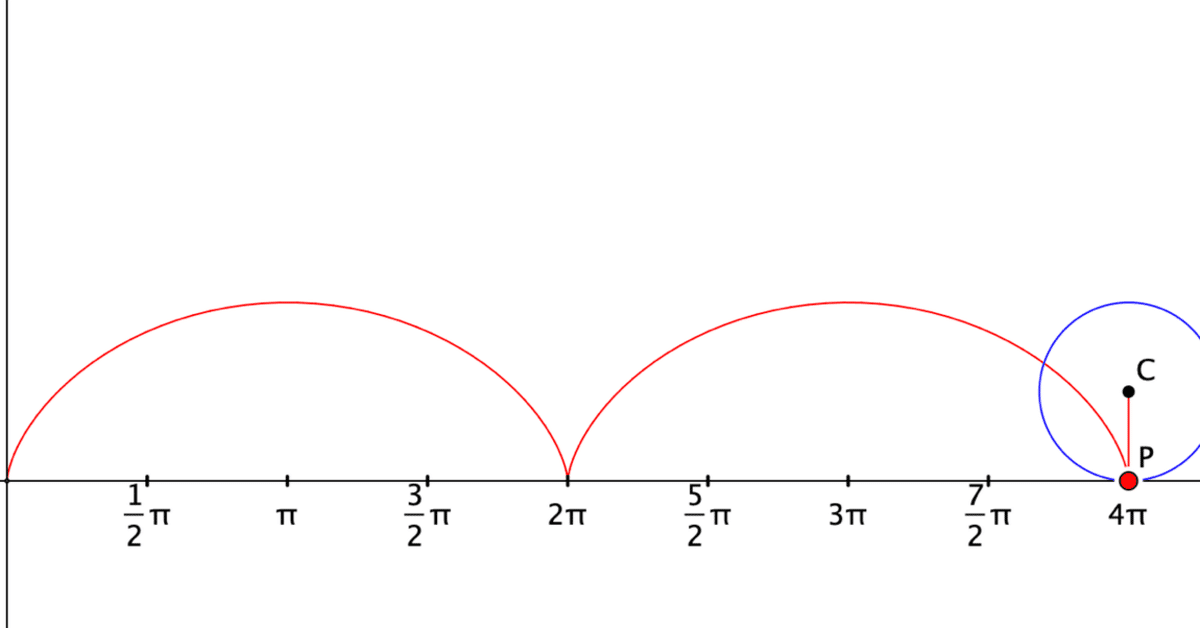
次の図がおなじみのサイクロイド。

点Pの位置を円周上からはずすとトロコイドといいます。(冒頭参照)
内トロコイド(ハイポトロコイド)

外トロコイド(エピトロコイド)
それぞれの方程式を導出しましょう。なお,高校の数学の教科書に載っている方法は一般性がないので却下です。
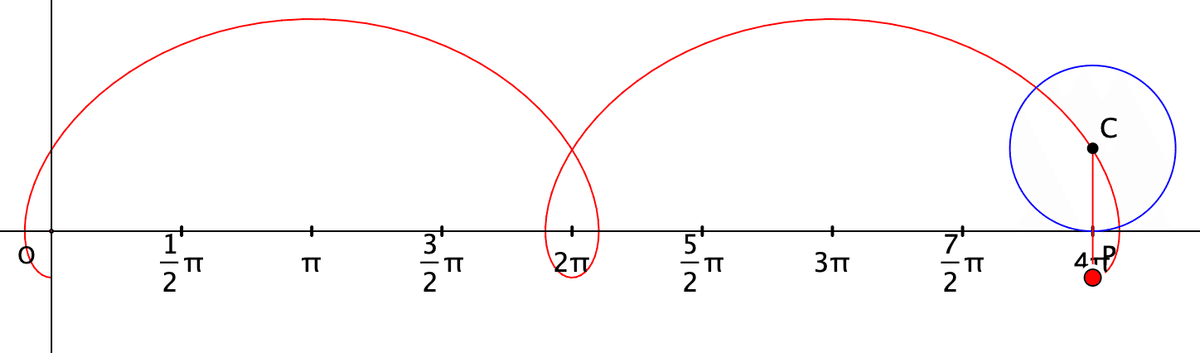
円がθだけ回転した図です。

円の中心が横方向に動いた道のり(赤い線)と,点Pが回転した道のり(弧の長さ)が等しい(すべらずに回転する)ので,Cの座標は$${(r \theta,r)}$$ です。
つぎに,円の中心を原点と見て,Pの位置を考えると,出発点が$${\dfrac{3}{2}\pi}$$ のところなので,$${\left( r\cos \left( \dfrac{3}{2}\pi-\theta\right), r\sin \left( \dfrac{3}{2}\pi-\theta\right)\right)}$$ になります。
したがって,点Pの座標は
$${x=r\theta+r\cos \left( \dfrac{3}{2}\pi-\theta\right)}$$
$${y=r+r\sin \left( \dfrac{3}{2}\pi-\theta\right)}$$
となります。三角関数の部分を加法定理で展開して整理すると,
$${x=r(\theta-\sin \theta)}$$
$${y=r(1-\cos \theta)}$$
となります。Pの位置をベクトルの和として$${\overrightarrow{\rm OP}=\overrightarrow{\rm OC}+\overrightarrow{\rm CP}}$$ と考えることもできます。
ここで大切なのは,結果の式よりも,その一つ前の式です。 $${ \dfrac{3}{2}\pi-\theta}$$ のところに,考え方が現れているからです。ここを理解すれば,円周上を回転するエピサイクロイドやハイポサイクロイドでも式を導出することができます。高校の数学の教科書ではこの方法をとっていないので,教科書のやり方ではエピサイクロイドの式を出すのが大変です。
点Pが円周上でない場合は,Cの位置は同じなので,CPの長さを pr とでもすれば, $${x=r\theta+pr\cos \left( \dfrac{3}{2}\pi-\theta\right)}$$
にすればいいわけです。
では,Cinderellaで動くものを簡単に作ってみましょう。
画面下の磁石ツールをクリックして,背景の座標軸と方眼を表示しておきます。
「半径付き円を加える」ツールで(0, 2) を中心とし,原点を通る円を描きます。
「線分を加える」ツールで,(0, 2)と原点を結んだ線分を描きます。

この円をころがすのですが,Cinderellaの作図ツールだけではできないので,CindyScript でプログラムを書きます。「スクリプト」メニューから「CindyScript」を選び,次のように各スロットにコードを書きます。
・Initializaition スロットに t = 0;
・Timer Tick スロットに t = seconds();
・Simulation Start スロットに resetclock();
・Draw スロットに
r = 2;
A.xy = [r * t, r];
B.xy = A.xy + r*[cos(3pi/2-t), sin(3pi/2-t)];
Shift+Enter で実行すると,画面左下にコントローラが現れ,プレイボタンを押すと円が回転していきます。このときの点Bの軌跡がサイクロイドです。

ストップボタンを押すと停止しますが,元の位置に戻すには,スクリプトを再実行します。再実行しなくても元に戻したり,軌跡のグラフを描いたりするには,さらにコードを追加していくわけです。
・ストップボタンで元に戻すには
Simulation Stop スロットに t = 0 を書く。
・グラフを描くには,Drawスロットに
f(t):=[r*(t - sin(t)), r*(1 - cos(t))];
plot(f(#),stop -> t);
を追加します。

サイクロイド・ハイポトロコイド・エピトロコイドを,点Pの初期位置をインタラクティブに変更してアニメーションで描くものを作りました。
また,つぎの「曲線の事典」のページには,作図器が載っています。
スクロールしていくと,サイクロイドがあります。
エピサイクロイド・ハイポサイクロイド
動円が,直線上ではなく定円の円周上を動くときの点Pの軌跡です。
動円が定円の外側を動く場合がエピサイクロイド,内側を動く場合がハイポサイクロイドです。
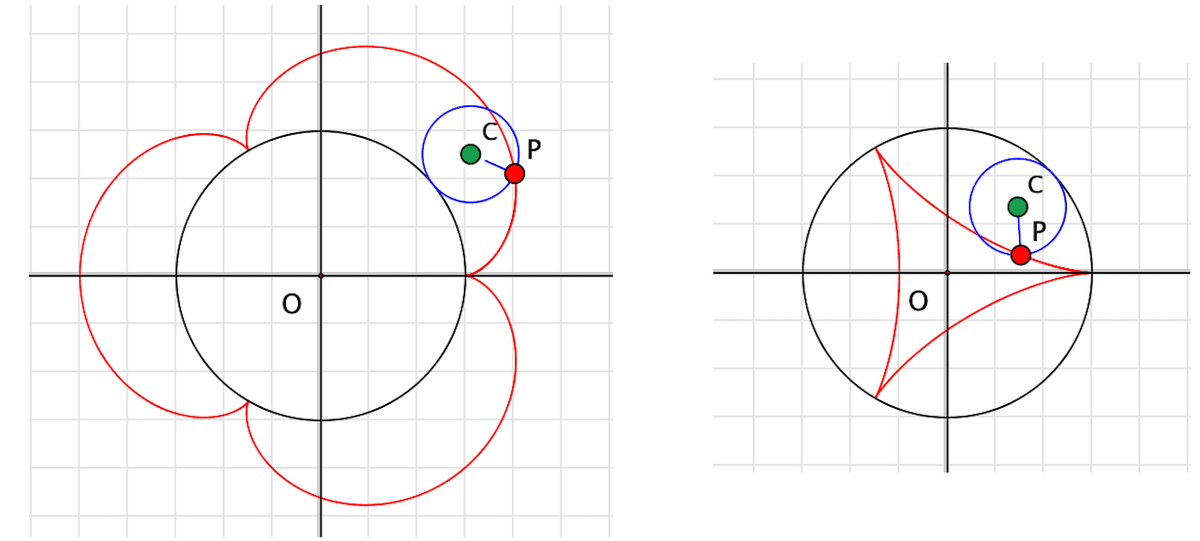
定円と動円が同じ大きさのときのエピサイクロイドはカージオイドといいます。カージオイドは極方程式でも表されたり,リマソンの一種ともいいます。
定円と動円の半径比が4:1のときのハイポサイクロイドはアステロイドといいます。アステロイドもいろいろな方程式があります。

では,エピサイクロイドの式を導いてみましょう。
次の図は動円がθだけ回転したものです。「すべらないように」回転していくので赤い弧の長さは同じです。

定円上の弧は $${R \theta}$$,動円での扇形の中心角を$${\alpha}$$ とすると,動円の弧の長さは $${r \alpha}$$ です。動円で,Cを中心としたときのPの位置を考えると ,Pの角は $${\theta-\pi+\alpha }$$ になります。$${R \theta=r \alpha}$$ から $${\alpha=\dfrac{R}{r} \theta }$$ で置き換えて,加法定理で展開した式を整理すると
$${x=(R+r)\cos \theta+r \cos \dfrac{R+r}{r}\theta}$$
$${y=(R+r)\sin \theta-r \sin \dfrac{R+r}{r}\theta}$$
となります。
ハイポサイクロイドは内側を回りますので,動円上の点Pはエピサイクロイドのときと逆回り,時計回りに回ります。

エピサイクロイドと同様,定円上の弧は $${R \theta}$$,動円での扇形の中心角を$${\alpha}$$ とすると,動円の弧の長さは $${r \alpha}$$ です。動円で,Cを中心としたときのPの位置を考えると ,Pの角は $${\theta-\alpha }$$ になります。$${\alpha=\dfrac{R}{r} \theta }$$ で置き換えて,加法定理で展開した式を整理すると
$${x=(R-r)\cos \theta+r \cos \dfrac{R-r}{r}\theta}$$
$${y=(R-r)\sin \theta-r \sin \dfrac{R-r}{r}\theta}$$
となります。
ペリトロコイド
動円の中心Cが,定円の半径の左端より左にあって,動円の方が大きい場合をペリトロコイドといいます。

方程式はハイポサイクロイドと同じです。
直線上を動くときに,円周上ではない点の動きを考えたように,円周上を動くときにも同じことをやってみましょう。


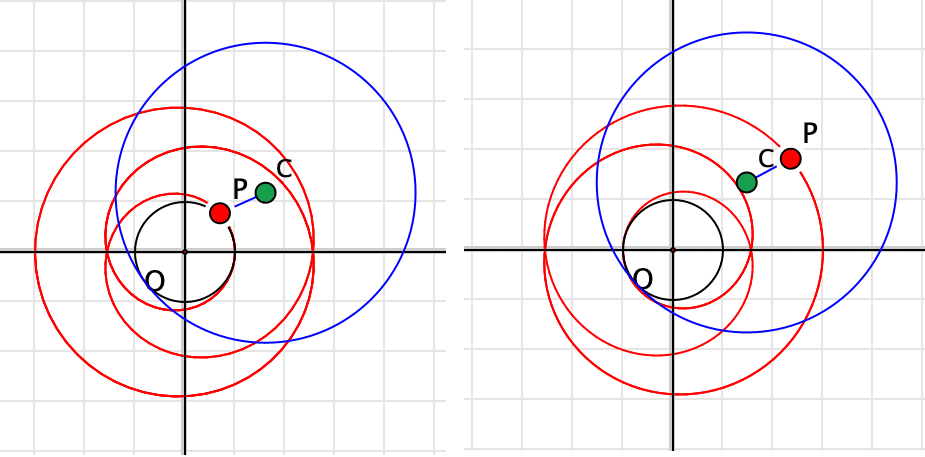
CとPの位置関係によってさまざまな図ができます。
ハイポサイクロイドで,Pの位置を定円より少し内側にしたものは,玩具としても売られているスピログラフになりますね。やってみましょう。
点C,点Pの初期位置をインタラクティブに変更してアニメーションで描くものを作りました。
放物線上のトロコイド
円が移動する軌道を放物線にとってみましょう。円盤を投げ上げた場合です。円盤でなくても回転するものならば構いません。たとえばトンカチ(カナヅチ)。「日常にひそむ数理曲線」(佐藤雅彦:小学館)には、トンカチを投げ上げた場合の図があります。トンカチの重心は放物線を描き、先端はトロコイドを描くのです。次の図は,これをCinderella で作ったものです。

トンカチでなく円の場合。点Cは円の中心。放物線上を動きます。重力加速度は9.8m/ss です。点Pは角速度ωで円C上を回ります。ωが正のときは反時計回りに,負のときは時計回りに回ります。

図では,スライダやボタンを作ってありますが,要は次の2つの方程式です。放物線と点Pの位置。vx は横方向の速さ, vy は縦方向の初速, g は重力加速度,ωは点Pの角速度です。
hx(t):=vxt;
hy(t):=vyt - 1/2gt^2;
fx(t):=hx(t) + rcos(ωt);
fy(t):=hy(t) + rsin(ωt);上の図では,Cの投射速度をベクトルで設定できるようになっています。角速度はスライダ。円の大きさも円周をドラッグすれば変えられます。次のリンク先をひらけば,このアプリケーションを実行できます。
