
Cinderellaでカオスを描く:微分方程式を解く
ローレンツアトラクタの節の最初に例として示したMathematicaでは、微分方程式を入力してそれを解かせています。MathematicaではNDSolveという微分方程式を解く関数を用いています。NDSolveのチュートリアルに、次のように書かれています。
NDSolveでは解を求めるために反復手法が使われる。それは、xのある値を始点とし、一連の刻みをとりながらxminからxmaxの範囲をくまなく探索していく
この、「反復手法」に、オイラー法とルンゲクッタ法があります。ここでは、オイラー法について考えます。高校数学の教科書にある「微分」「微分方程式の解法」から始めて、Cinderella.2で実験しながら、カオスを探究するのに必要な方法を考えていきましょう。ルンゲクッタ法については詳しく言及することはしません。
微分の定義と記法
まず、微分の定義と記法、その意味をグラフで復習しておきます。
関数$${f(x)}$$の点$${(a,f(a))}$$ における微分係数を次のように定義します。
$${f'(a)=\displaystyle\lim_{b \to a}\dfrac{f(b)-f(a)}{b-a}}$$
微分係数は、図形的には、曲線 $${y=f(x)}$$ の点$${(a,f(a))}$$における接線の係数となります。したがって接線の方程式は $${y=f'(a)(x-a)+f(a)}$$です。
$${a}$$ を変数にすれば導関数の定義になります。
CindyScript には,微分をする関数 d() が用意されています。そこで,$${f(x)}$$ を微分して接線の式を作り,$${f(x)}$$ のグラフと接線を表示するものを作ってみましょう。
まず準備として、座標軸と方眼を表示しておき、「直線を加える」モードでx軸上に直線ABを引き、「点を加える」モードで直線AB上に点Cを取ります。「要素を動かす」モードで、点Cが直線ABすなわちx軸上を動くことを確かめておきましょう。

準備ができたら次のスクリプトを書きます。
f(x):= x^2;
f1(x):= d(f(#), x);
s(x,t):= f1(t)*(x - t) + f(t);
t = C.x;
plot(f(x));
plot(s(x, t), start->t - 1, stop->t + 1, color->[1, 0, 0], size->2);1行目は関数の定義。ここでは簡単な2次関数です。
2行目は導関数の定義。ただし、limをとる関数はないので、CindyScriptにある微分の関数 d() をそのまま使います。
3行目は接線の方程式の定義
1行空けて、4行目では点Cのx座標を変数tとして取り込んでいます。
5行目は関数f(x)のグラフを描画
6行目で点$${(t,f(t))}$$における接線を赤で表示します。

点Cを動かすと、接線も動きます。これで、「点の近くでは、曲線と接線はほぼ一致する」ことを体感しましょう。
微分した関数を使ってもとの関数を近似する
「点の近くでは、曲線と接線はほぼ一致する」ということは、微分係数 を使って、曲線上で,ある点に近い点すなわち関数の値が求められることです。高校の数学Ⅲでは,近似式としてつぎの式を学びます。
微分係数の定義より $${\displaystyle \lim_{h \to 0}\dfrac{f(a+h)-f(a)}{h}=f'(a)}$$
したがって$${h}$$ が0に近いときは
$${\dfrac{f(a+h)-f(a)}{h} \fallingdotseq f'(a)}$$
すなわち
$${f(a+h)\fallingdotseq =f(a)+hf'(a)}$$ ・・・(*)
これを使って,すぐ近くの点を次々にとっていけば、導関数からもとの関数の値が次々に求められることになります。
では、この原理に基づいて関数値を求めていったものと、関数の実際の値を比較するスクリプトを書いてみましょう。
f(x):= 1/2*x^2;
f1(x):= d(f(#),x);
plot(f(x));
h=0.1;
g(x,y):= y + h*f1(x);
a = 0;
b = 0;
repeat(40,
draw([a, b], size->2);
a = a + h;
b = g(a, b);
);1行目、もとの関数の定義です。係数が$${\frac{1}{2}}$$ の2次関数。
2行目、その導関数をCindyScriptの関数を用いて求めています。
3行目 $${f(x)}$$ のグラフを描きます。
4行目、先ほどの式の$${h}$$の値。
5行目、導関数を用いて、あるx,y から次のyの値を計算します。先ほどの(*)
6,7行目 出発点の x , y の値です。両方とも0にしています。
8行目〜12行目、すぐ近くの値を計算する、という操作を40回繰り返します。xの増加量hが0.1ですので、始めのxの値からx+4まで,0.1刻みで求められることになります。9行目、計算した点をプロットします。
10行目、aの値をhだけ増やします。グラフ上ではすぐ近くの点です。
11行目、aがhだけ増えた点のyの値を(*)を使って計算します。
実行結果は次のようになります。緑の点が、導関数から計算したもとの関数の値を示す点です。$${f(x)}$$ のグラフとだいぶ近いことがわかります。

$${f(x)}$$を3次関数$${f(x)=x^3-x^2-x}$$にしてみましょう。
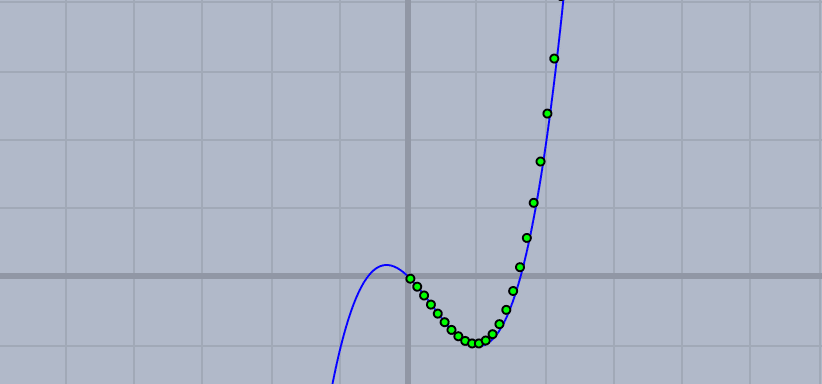
hの値を0.05 にしてみましょう。

もとの曲線により近づいていますね。
微分方程式を数値的に解く:オイラー法
導関数を表すのに、$${\dfrac{dy}{dx}}$$ を使います。
先ほどの例では
$${\dfrac{dy}{dx}=x}$$ ・・・ ①
から $${y=\dfrac{1}{2}x^2}$$ ・・・ ②
の関数値を次々に求めていきました。使った式は
$${f(a+h)\fallingdotseq =f(a)+hf'(a)}$$ ・・・(*)(再掲)
でした。
①の式は、導関数の式ですが、これを方程式と考えて微分方程式といいます。ここから、もとの関数を求めることを「微分方程式を解く」といいます。この例はもっとも簡単なもので、積分すれば①から②は求められます。
$${\displaystyle \int x dx=\dfrac{1}{2}x^2+C}$$
このCを積分定数といいますね。2つの値p,q を用いて「x=p のとき y=q」という条件をつければ、この積分定数の値は決まります。この条件を初期条件といいます。
さて、先ほどやったのは何かというと、積分をしないでもとの関数の値を求めた、ということです。積分を行なって求めるのを「解析的に解く」といい、値を次々に求めていってもとの関数がどんな関数かを調べることを「数値的に解く」といいます。先ほどの例でわかるように、数値的に解いた場合、解析的に解いた「解」と、完全には一致しません。近似的に解けた、ということです。
では、①の右辺がxではなく,yの場合の微分方程式を解いてみましょう。高校数学では発展的内容となっています。初期条件を x=0のときy=1とすると次のようになります。
$${\dfrac{dy}{dx}=y}$$ より $${\dfrac{1}{y}dy=dx}$$ なので両辺を積分して
$${\displaystyle \int \dfrac{1}{y}dy=\displaystyle \int dx }$$
$${\log|y|=x+C}$$
$${y=\pm e^{x+C}}$$
$${\pm e^C=A}$$ とおくと $${y=A e^x}$$
初期条件は x=0, y=1 なので,代入すると $${A=1}$$
よって $${y=e^x}$$
これが解析的な解です。
では,前と同じように数値的な解でグラフにしてみましょう。
g(x,y) の定義を g(x,y):=y+h*y に変え,初期条件を a=0; b=1; とします。
解析的な解の$${y=e^x}$$ のグラフも描いて比較しましょう。
f(x):= exp(x);
plot(f(x));
h = 0.05;
g(x,y):= y+h*y;
a = 0;
b = 1;
repeat(40,
draw([a,b], size->2);
a = a + h;
b = g(a, b);
);次のようになりました。

このようにして数値的に微分方程式を解く方法を「オイラー法」といいます。
オイラー法は簡単なのですが誤差も大きいのです。上の例でみても,グラフから少しずつ点が離れています。
媒介変数表示と微分方程式
半径$${r}$$の円は,次のように媒介変数で表されます。
$${x=r \cos t,y=r \sin t}$$
これを $${t}$$ で微分すると
$${\dfrac{dx}{dt}=-r \sin t = -y }$$
$${\dfrac{dy}{dt}=r \cos t = x }$$
となります。$${x,y}$$ は$${t}$$ の関数ですが,微分すると$${t}$$ の入らない式になることに注意してください。
これを使って,数値的にこの微分方程式を解いて円を描いてみましょう。半径は$${r=2}$$ ,描き始めの点(初期値)は$${(2,0)}$$とします。$${0 \leqq t \leqq 2 \pi}$$ ですので,それに合わせて繰り返しの数を決めます。
h = 0.05;
fx(x,y):= x + h*(-y);
fy(x,y):= y + h*x;
x = 2;
y = 0;
repeat(126,
draw([x, y], size->1);
xx = fx(x, y);
yy = fy(x, y);
x = xx;
y = yy;
);次のように描かれますが,円がしっかり閉じていません。

hを 0.01 にして繰り返しを繰り返しを628回にすると次のようになります。
さっきよりいいですが,やはり少しずれます。

ルンゲ・クッタ法
オイラー法よりよい近似が得られるものとしてルンゲ・クッタ法があります。よく使われるのは4次のルンゲ・クッタ法で,次の式を使います。
$${k_1 =hf(x_n,y_n)}$$
$${k_2 =hf(x_n+\frac{h}{2},y_n+\frac{k_1}{2})}$$
$${k_3 =hf(x_n+\frac{h}{2},y_n+\frac{k_2}{2})}$$
$${k_4 =hf(x_n+h,y_n+k_3)}$$
として,
$${y_{n+1} =y_n + \frac{1}{6}(k_1 +2k_2 +2k_3 +k_4)}$$
で次の値を求めます。
これを円の方程式に適用します。上の式は$${y}$$が$${x}$$の関数のときの式なので,円では媒介変数表示で$${x,y}$$がそれぞれ$${t}$$の関数になるのでした。微分すると $${\dfrac{dx}{dt}= -y }$$ でしたが,これだと $${t}$$がなくて$${y}$$ の式で,ルンゲ・クッタ法だとややこしくなるので, $${\dfrac{dx}{dt}=-r \sin t , \dfrac{dy}{dt}=r \cos t }$$の方を使います。
h = 0.02;
r = 2;
fx(t,x):= -r*sin(t);
fy(t,y):= r*cos(t);
t = 0;
x = r;
y = 0;
repeat(314,
draw([x, y], size->0.2);
k1 = h*fx(t, x);
k2 = h*fx(t + h/2, x + k1/2);
k3 = h*fx(t + h/2, x + k2/2);
k4 = h*fx(t + h,x + k3);
xx = x + (k1 + 2*k2 + 2*k3 + k4)/6;
k1 = h*fy(t, y);
k2 = h*fy(t + h/2, y + k1/2);
k3 = h*fy(t + h/2, y + k2/2);
k4 = h*fy(t + h, y + k3);
yy = y + (k1 + 2*k2 + 2*k3 + k4)/6;
x = xx;
y = yy;
t = t + h;
);つぎのようにきれいにつながりました。

→ Cinderellaでカオスを描く:序と目次 に戻る
