
インドラの真珠:帯 その1
前節の最後にごらんいただいた極限集合は大変魅力的なものでした。しかし、4つの円を自由に動かしてこの図を見つけることはなかなか困難でしょう。ここでは、自由度を少し制限して、特別な場合から始めることにします。それは、4つの円のうち2つの半径を無限大にしてしまうのです。半径が無限大の円の円周は、直線であると考えましょう。この2本の直線は平行であることにします。
リンク先を開くと次の画面になります。

平行な直線が2本と円が2つ,青で描かれています。描画色のスライダで色を変えることができます。
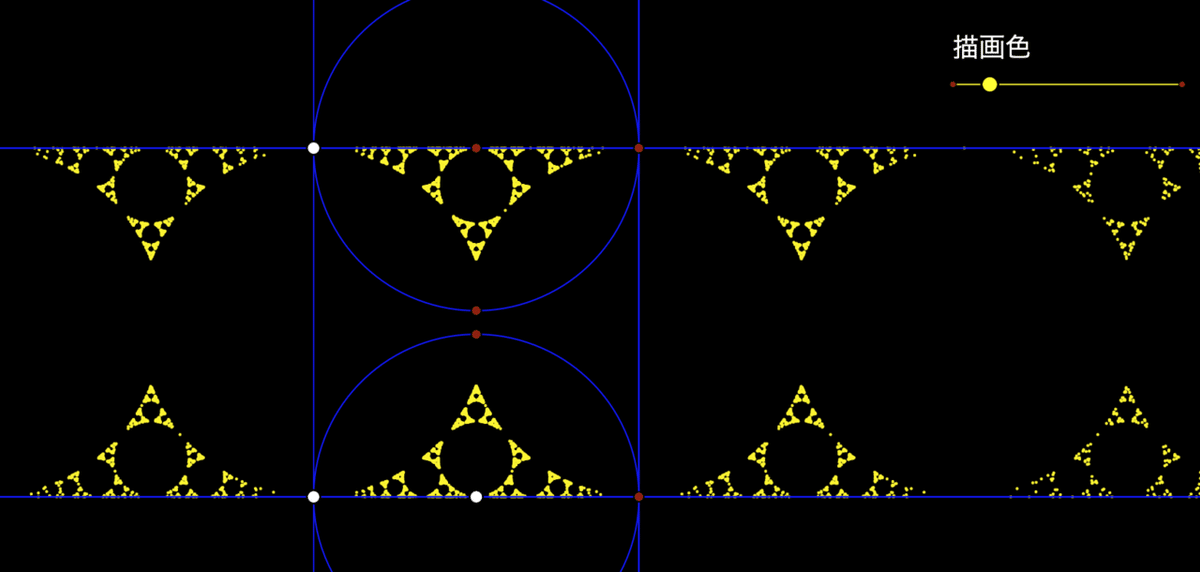
白い点をドラッグすると,円の位置,大きさを変えることができます。
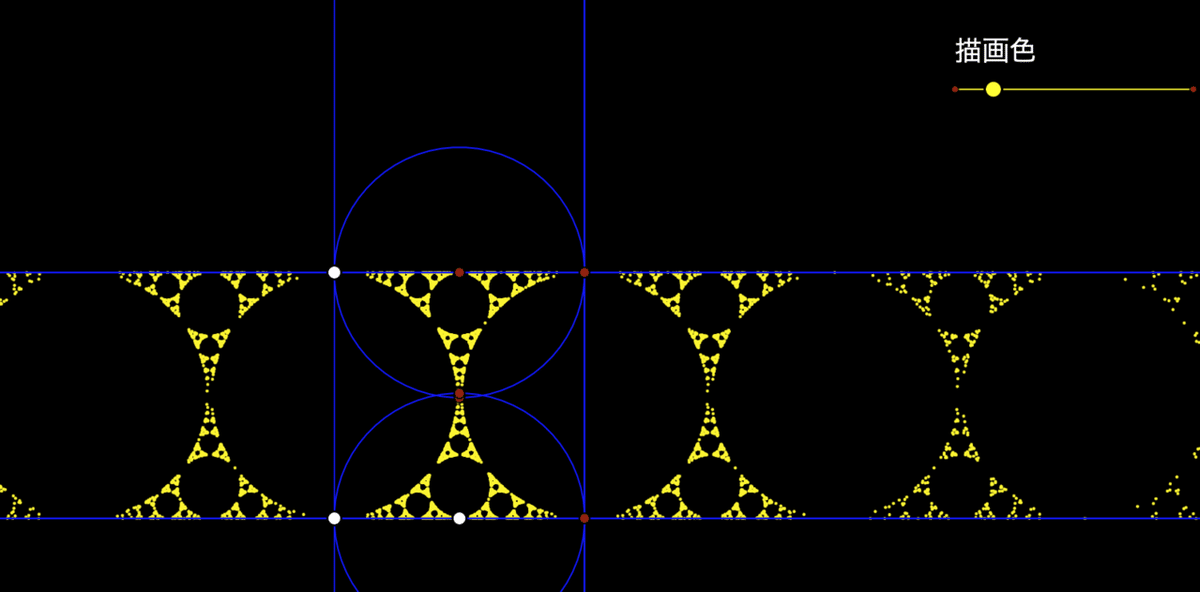
さて,中央の円はそれなりに描かれていますが,両端は薄くなっています。
CindyScriptでプログラムを書いてCindyJSに書き出すのだと,このあたりが限界のようです。見出し画像と違いますね。CindyGLを使うと次のように表示することができます。この場合は,作図のアルゴリズムが違います。後ほど,「おばあちゃんのレシピ」で説明します。

Cinderellaの作図ツールで作ると,プログラムを書かずに見出し画像のようなきれいな図が簡単にできます。
------------------------
ここからは,Cinderellaのツールだけでこの図を作る方法を説明します。でき上がりの図はつぎのようになります。 色を変えると見出し画像のようになります。
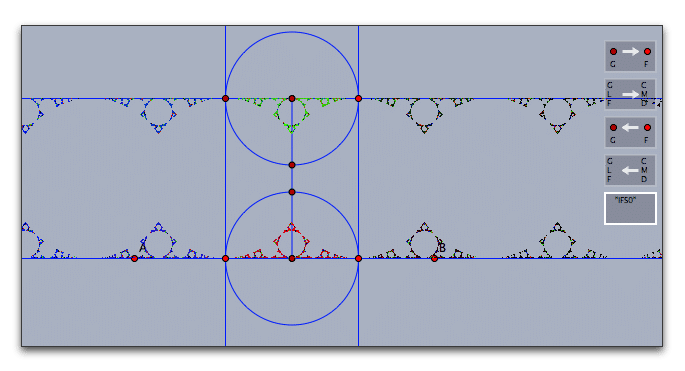
まず、円で定義していたメビウス変換が、2本の平行線ではどうなるのかを見ておきましょう。
まず、平行線ツールと垂線ツールを用いて、次のような図を描きます。
6点が長方形状になっています。平行線ツールだけを用いて、平行四辺形にしても同じ結果になります。
変換に使う適当な図(たとえば三角形)を描いておきます。
モードメニューの「変換」「メビウス変換」を選び、3組の点を使ってメビウス変換を定義します。
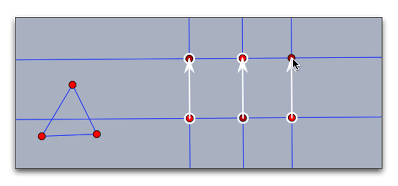
描画の順序は問いませんので、ラベルは非表示にしています。
三角形の3辺を選択して(Shiftキーを押しながらクリック)メビウス変換のアイコンをクリックします。像ができます。
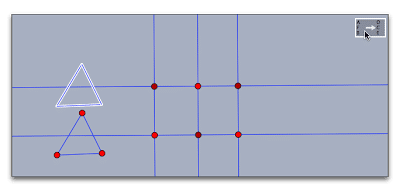
その結果は平行移動であることを確かめましょう。
メビウス変換の定義に用いた6点(実際には可動な3点)を動かしたり、三角形の頂点を動かしたりしてみます。

なお、平行線上の3点といっても、次のような場合には平行移動にはなりませんので注意しましょう。
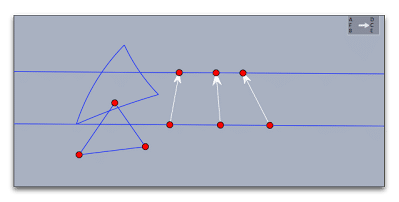
つまり、対応する3組の点を結ぶ線分も平行のときに、平行移動になるということです。
前節で4つの円を使いましたが、このうち2つを平行な2本の直線にします。(半径が無限大の円と思うことにしましょう)
あとの2つの円は同じ大きさということにして、次の図のように作図し直します。
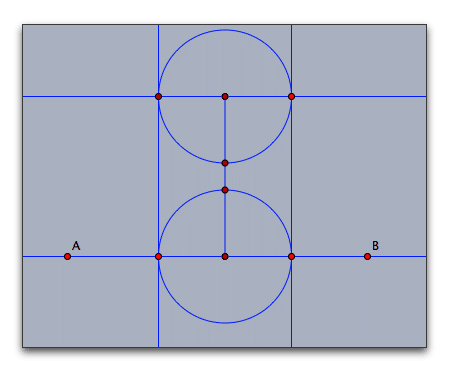
点A,Bは最初にとった直線を定義する点です。ここから、平行線ツールや垂線ツール、中点ツール(円の中心を求める)、交点ツールを用いて作図します。ラベルは非表示にしています。
次にメビウス変換を定義しますが、上図の平行線の場合は平行移動と同じでしたので、モードメニューの「変換」から「平行移動」を選んで、上か下のどちらかをひとつ指定します。
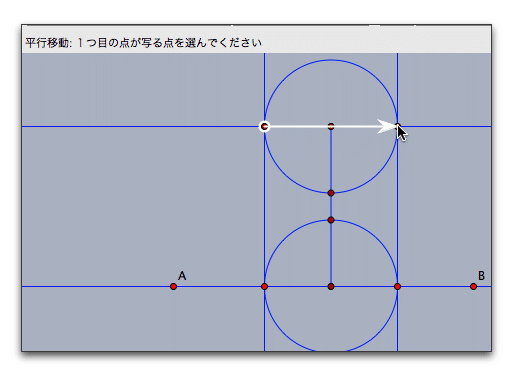
次に、上下の円でメビウス変換を定義します。
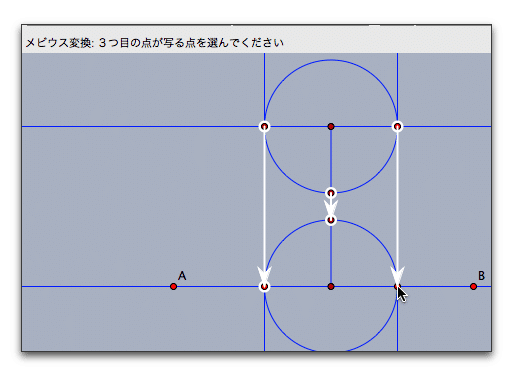
それぞれの逆変換を作って、全部で4つの変換からなる反復関数系を定義すれば完成です。
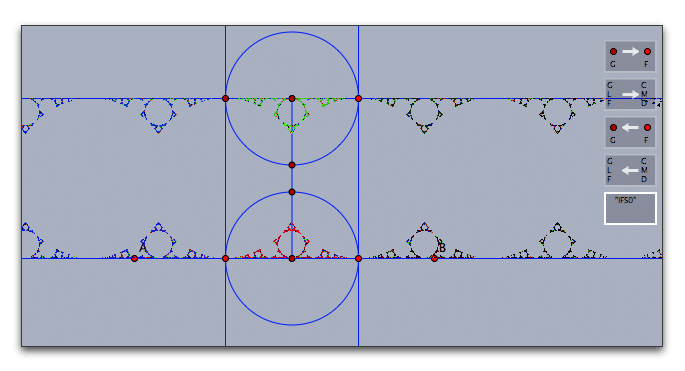
あとは、インスペクタで背景の色を変えたり、反復関数系でできる図形の色を変えたり、円の大きさを変えたりして楽しみましょう。
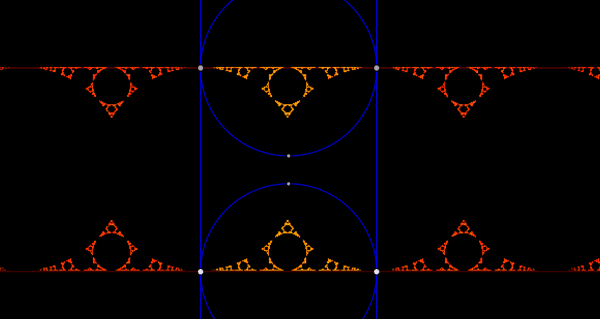
→次節:帯 その2
→インドラの真珠:目次 に戻る
