
Cinderellaで数学:いろいろな曲線:様々な楕円作図器
「曲線の事典」(礒田正美他編著:共立出版 2009)に掲載されている,プロクロス,ダヴィンチ,スコーテンの楕円作図器です。いずれもシンプルな構造で楕円を作図します。
プロクロスの作図器
点A,Bは十字に組み合わされたガイドに取り付けられ,それに沿って滑り動く。2点A,Bを通る直線a上の描画点Pを半直線ABのBの先にとる。このとき、点Pは,軸の長さがそれぞれ 2PA,2PBとなる楕円をかく。

右の図では,「十字に組み合わされたガイド」がx軸,y軸のように直線で描かれていますが,作図器の写真を見てわかる通り,文字通り「十字に組み合わされたガイド」であって短いものです。したがって,線分としてこの2本を描いておきます。また,右の図にある円は必要ありません。この円と点Mは,このあとの解説で,Pの軌跡が楕円であることを説明するためのものです。
作図器の動作を考えると,PAとPBの長さは一定であることがわかります。また,ガイドに沿って動かすのは点Aの方であることもわかります。溝に沿った棒があるからです。そこで,軌跡ツールで,動かす点をA,軌跡を描く点をPと指定できるように作図しましょう。点の名前は図に合わせて変え,作図に使った補助円はそのままにしてあります。

軌跡ツールで,動かす点をA,軌跡を描く点をPとすると,楕円の一部が描かれます。点Bが縦の軸より左にある範囲です。
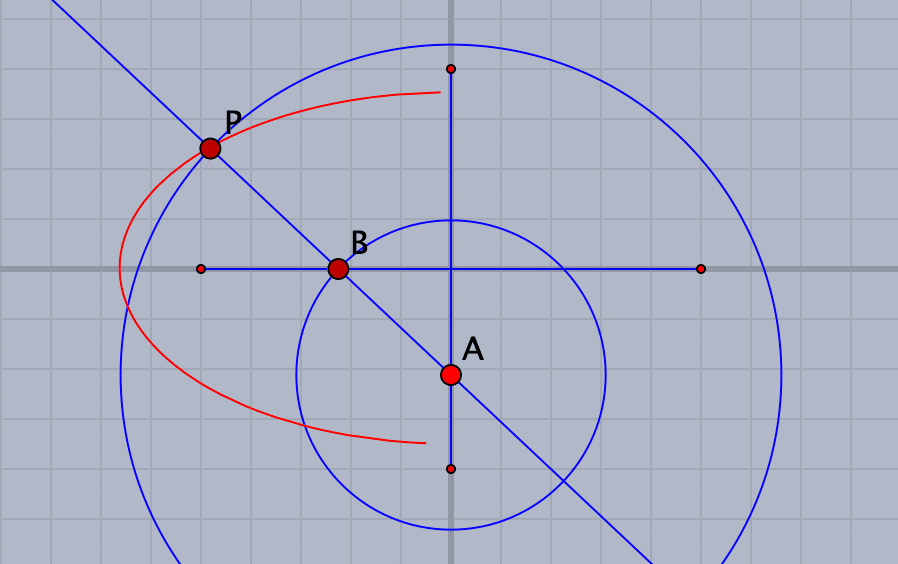
ところで,前述のように,ガイドに沿って動かせるのは,点Aが載っている棒なので,点Aそのものは十字の範囲を少し越えることができます。すると点Bは右の方にも行けるわけです。
点Aを載せる線を線分でなく直線にすると,軌跡ツールで軌跡を描いたときに楕円全体が描かれます。

本では,このあとにPの軌跡が楕円になる理由を説明しています。ここで,図の円と点Mが使われます。すなわち,△OABは直角三角形で,ABの中点をMとすると$${\rm{OM}=\dfrac{AB}{2}}$$ になるので,Mは円周上を動き,Pの軌跡は,Mによる円を,軸方向にそれぞれ$${\dfrac{\rm{AP}}{\rm{AM}}}}$$倍,$${\dfrac{\rm{BP}}{\rm{BM}}}}$$倍した楕円になる,という説明です。 次の図で確かめましょう。

ダヴィンチの作図器
菱形 OABCがあり,頂点Oは固定。対する頂点Bは点Oを通る直線 r 上を動く。点Bが直線 r 上を動くとき,点Aと点Cは中心O,半径OAの半円をかき,棒 a 上の点Pは(同様に棒b上の点Qは)直線 r を対称軸にもつ楕円の1/4をかく。点E,Fはそれぞれa,bと点Oを通る直線 r に垂直な直線との交点で AE=CF=OAとなっている。

作図器の写真を見ると,OABCが菱形かどうかは判然としませんが,AE=CF=OAとなるためには菱形である必要があるのです。Cinderellaで作図して,菱形でない場合にどうなるかをやってみるとわかります。
OABCを菱形にするには,OBの垂直二分線を引いて,その上にA,C をとればいいのですが,OABCが菱形になる場合とならない場合を比べられるように,2つの円を用いて作図してみましょう。
① 縦横の直線を背景の座標軸に合わせて描く。線分でも構いません。直線のときと線分のときとでは,軌跡の楕円の描画範囲が変わります。
② 縦の直線上に点をとりBとする。
③ 原点と点Bを中心とする円をそれぞれ描く。
④ 2つ円の交点をとり,A,Cとし,点Bと結んだ直線を描く。
⑤ 点P,Qをとるために,Bを中心とする円をもう一つ描き,④の直線との交点をP,Qとする。
⑥ 軌跡ツールを選び,動かす点としてB,軌跡を描く点としてPを選びます。
次の図が,③の2つの円の半径を同じにした場合で,OABCは菱形になります。楕円は下方まで描かれていますが,下方はBの可動域から外れるので無視します。

次の図は,③の2つの円の半径を変えた場合で,OABCは菱形にならず,軌跡は楕円ではなくなります。(やはり下方は無視します)

スコーテンの作図器
直線g上に固定点Oと可動点B,点Bを通る直線上にOA=ABをみたす点Aをとる。点Aが点Oを中心に回転するとき,線分BP上の各点で各々楕円をかく。また,AQ=AB=OAをみたす直線 BP 上の点Qは直線gに垂直で点Oを通る線分をかく。彼らの方法は,前出のプロクロスの場合と実質的に同じである。

これはシンプルなのでCinderellaですぐ描けるでしょう。「可動点B」となっていますが,Cinderellaの用語ではBは従属点です。「点Aが点Oを中心に回転するとき」となっているので,Aが自由点で,上の右図にはありませんが点Oを中心とする円を描いて,その上にAをとります。このことは,作図器の写真からわかります。それから,Aを通る垂線を引き,これを鏡として点Oの鏡映点BをとればAB=OAとなります。点Qは作図上は不要です。

3つの作図器のうち,ダヴィンチのものを模して作りました。(見出し画像)
