
「情報関係基礎」教材化(2):2007年ブロック落とし
元の問題(以下,オリジナル)はWebの https://sites.google.com/a.ipsj.or.jp/ipsjjn/resources/JHK からダウンロードできる。これを題材に教材を作る。
以下は,その教材プリントと実習用ファイルの例である。
===============================
問題
横8,縦4の升目があり,そのひとつひとつを「ブロック」という。このブロックには,整数または,演算記号「+」「ー」「×」が書かれている。
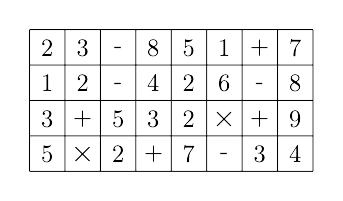
次の手順1〜3によりブロック落としをする。
手順1 計算は最下段のみを対象とし,左から順に計算可能な組み合わせを
調べる。計算可能な組み合わせは3つのブロックで,中央が演算
ブロック,左右が整数ブロックの場合である。その演算により,
演算ブロックを結果の整数で置き換え,左右の数ブロックを取り除く。
この作業を右端まで繰り返し手順2に進む。
手順2 手順1の後,取り除かれたブロックがある場合は,その上のすべての
ブロックを1マスずつ下に移動させ,手順3へ進む。
手順3 手順1で,一度も計算をしなかった場合,ゲームは終わる。そうで
なければ手順1へ戻る。
次の例は,この手順を繰り返し,最終的にいくつかのブロックが残る様子を示す。

このブロック落としのプログラムを作る。
プログラムの構成
オリジナルの問題には,手順1,2を行う部分と全体の手順が穴埋めの形になっている。これらのうち,手順1,手順2は関数として作り,一部を空欄にして問題とする。
手順1の計算 関数 calc()
手順2ブロックを落とす 関数 drop()
この他に,問題の中で使う関数,描画のためのプログラムが必要である。
isop() 演算ブロックかどうかを判定するための関数
dispblock(pt,mat) 8×4のマスと,ブロックの内容を表示する
これらはあらかじめ作っておく。
したがって,全体の構成は次のようになる。
初期設定 ブロックの最初の状態をデータとして作る
関数 isop() の定義
関数 calc() ,drop() の定義(空欄あり)
全体の制御と画面表示dispblock()の定義(空欄あり)
初期設定
ライブラリのインポート
Numpy と Matplotlib を用いる。
import numpy as np
import matplotlib.pyplot as plt関数 isop(block) の定義 : 引数はブロックの内容
ブロックが演算子かどうかを判定する関数である。あらかじめ作っておく。
# block が演算ブロック +,-,* かどうかを調べる
def isop(block):
return(block == "+" or block == "-" or block == "*")画面表示をする関数 dispblock(mat) : 引数はブロックのリスト
あらかじめ作っておく。
def dispblock(mat):
# print(mat)
for y in range(4):
for x in range(8):
if mat[y][x] == "*":
wd = "×"
else :
wd = mat[y][x]
plt.text(x + 0.3,y + 0.4, wd,fontsize=20)
plt.xlim(0,8)
plt.ylim(0,4)
plt.yticks([1,2,3])
plt.grid()
plt.show()ブロックのリストの定義
ここから実習で生徒に書かせる部分を含む。ブロックははじめは簡単なものにしておいて動作を確かめ,動いたら定義を変えられるようにする。次の例は,さきほど示したものだが,はじめは元の問題にあるような簡単なものにしておくのもよいだろう。
T = [
[1,2,"*",4,5,"+",7,8],
[3,"+","-",5,2,"*","-",6],
[3,"+","-",3,5,"-","-",1],
[8,"+",6,5,4,3,"-",1]
]実習課題
手順1:ブロックの計算を行う関数 calc() の定義
実習課題で,丸数字に適するものを入れていく。配布テキストにはこのように丸数字で書いたものを印刷し,実習用ファイルでは単に空欄にしておくとよいだろう。
def calc():
global kosuu
global keisan
ret = 0
for x in range(1, ①):
if isinstance(T[0][x-1],int) and isop(T[0][x]) and isinstance(T[0][x+1],int):
if T[0][x] == ② :
T[0][x] = T[0][x-1] + T[0][x+1]
if T[0][x] == "*" :
T[0][x] = T[0][x-1] * T[0][x+1]
if T[0][x] == "-" :
T[0][x] = T[0][x-1] - T[0][x+1]
T[0][x-1] = ③
T[0][x+1] = ④
ret = ret + 1
keisan = keisan + 1
kosuu = kosuu - 2
return ret
この場合,③④は空文字になるのだが,空文字を “” で表すというのがわかりにくいかもしれない。そこで,T[0][x-1] の方は 「T[0][x-1] = “" // 空文字」としておくのもよい。また,「 if T[0][x] == "-" :」を「 if T[0][x] == ③ : 」として問題にしてもよいだろう。
なお,「global kosu」は,変数 kosu を関数外でも使っているので,「グローバス変数として扱う」という意味の宣言。
手順2:ブロックを落とす関数 drop() の定義
def drop():
for x in range(8):
if T[0][x] == ① :
for y in range(3):
T[y][x] = ②
T[3][x] = “”
空欄にする箇所は変更しても構わない。
メインプログラム
全体の手続きを作る。
オリジナルの問題では,変数 keisan ,kosuu の値を変更する部分をはじめのコードから抜いておき,最後に追加させる設問がある。この2つは,ブロック落としの実行そのものには影響がないので,あとから結果を表示させるものとして追加させてもよいだろう。その他,空欄を設けて全体の動きを考えさせてもよい。そこは,生徒の状況に応じて適宜設定する。
#main
dispblock(T) # 最初の状態
kosuu0 = 0
for s in range(4): # 空でないブロックの数をカウント
for t in range(8):
if T[s][t] != "":
kosuu0 = kosuu0 + 1
kosuu = kosuu0
keisan = 1
kai = 1
while kai > 0:
kai = calc()
drop()
if kai > 0 :
dispblock(T) # 途中経過も表示
print("計算回数は " + str(keisan))
このブロック落としは,プログラムができて終わりではなく,始めのパターンの制作も課題にするとよい。筆者は,授業後のある期間をとって,自由課題とした。提出した場合は実習点にプラスされる。条件は
・すべてのマスを埋める。
・最終的に下の1段だけが残り,できれば規則的な並びになるとよい。
・始めの状態で,最上段と最下段が規則的な並びになっているとよい。
[ 例 ] 最上段は1から8までの整数列である。
最下段は1だけが並んでいる。そのうち2つは演算ブロックである。
最終結果は最下段だけ残り,1から8まで順に並ぶ。
ただし,紙上でやることになり,決して簡単にできる課題ではないが,興味を持った生徒何人かが応募してきた。
中には円周率とネピア定数を用いたものもあり驚かされた。
全体のプログラム
穴埋めのない完成形を載せておく。
import numpy as np
import matplotlib.pyplot as plt
def dispblock(mat):
# print(mat)
for y in range(4):
for x in range(8):
if mat[y][x] == "*":
wd = "×"
else :
wd = mat[y][x]
plt.text(x + 0.3,y + 0.4, wd,fontsize=20)
plt.xlim(0,8)
plt.ylim(0,4)
plt.yticks([1,2,3])
plt.grid()
plt.show()
# block が演算ブロック +,-,* かどうかを調べる
def isop(block):
return(block == "+" or block == "-" or block == "*")
# ==== ここから下を作る ===========
T = [
[1,2,"*",4,5,"+",7,8],
[3,"+","-",5,2,"*","-",6],
[3,"+","-",3,5,"-","-",1],
[8,"+",6,5,4,3,"-",1]
]
# 計算を実行し,計算回数を返す
def calc():
global kosuu
global keisan
ret = 0
for x in range(1,8):
if isinstance(T[0][x-1],int) and isop(T[0][x]) and isinstance(T[0][x+1],int):
if T[0][x] == "+" :
T[0][x] = T[0][x-1] + T[0][x+1]
if T[0][x] == "*" :
T[0][x] = T[0][x-1] * T[0][x+1]
if T[0][x] == "-" :
T[0][x] = T[0][x-1] - T[0][x+1]
T[0][x-1] = ""
T[0][x+1] = ""
ret = ret + 1
keisan = keisan + 1
kosuu = kosuu - 2
return ret
# ブロックを下に落とす
def drop():
for x in range(8):
if T[0][x] == "":
for y in range(3):
T[y][x] = T[y+1][x]
T[3][x] = ""
#main
dispblock(T) # 最初の状態
kosuu0 = 0
for s in range(4): # 空でないブロックの数をカウント
for t in range(8):
if T[s][t] != "":
kosuu0 = kosuu0 + 1
kosuu = kosuu0
keisan = 1
kai = 1
while kai > 0:
kai = calc()
drop()
if kai > 0 :
dispblock(T) # 途中経過も表示
print("計算回数は " + str(keisan))