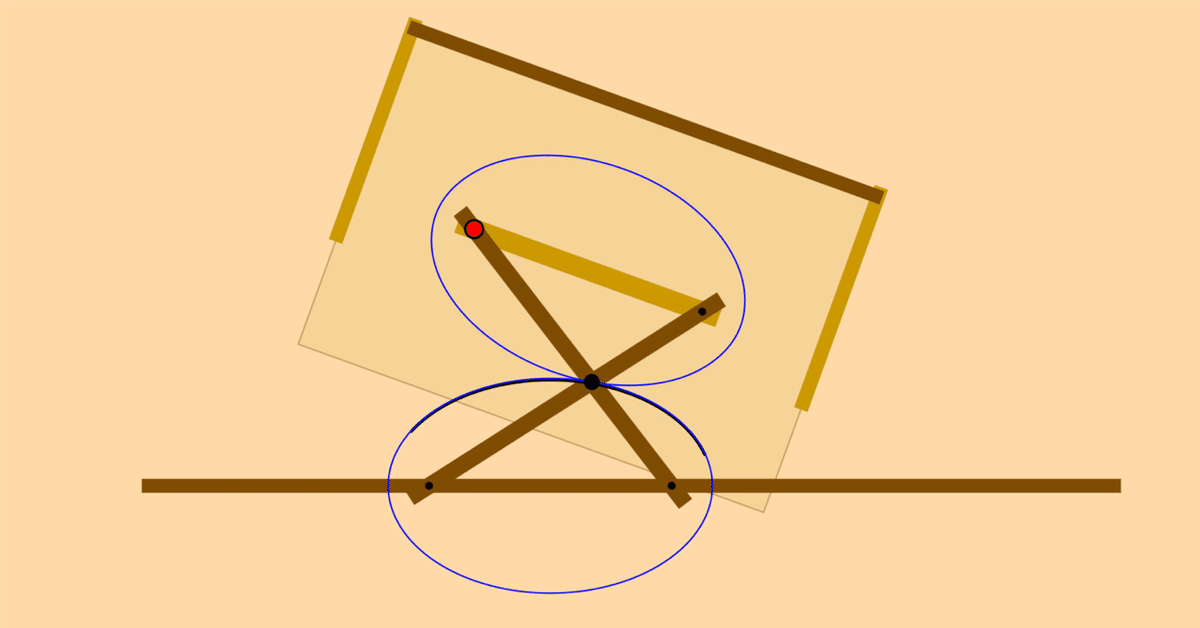
Cinderellaで数学:いろいろな曲線:転がり合う2つの円錐曲線
「曲線の事典」(礒田正美他編著:共立出版 2009)に掲載されている,「転がり合う2つの円錐曲線:周転曲線」です。
交叉平行四辺形ABCDがある。線分ABは平面$${\pi}$$上に固定され,線分CDは平面$${\pi}$$上にのった平面$${\tau}$$上にある。直線AD と直線BCの交点をPとする。
このあと,楕円の場合と双曲線の場合の2つが書かれていて,それぞれの作図器の写真があるのですが,書かれている条件は全く同じです。次は「楕円の場合」ですが,「楕円」を「双曲線」と置き換えただけで,双曲線の場合の写真と図があります。
点Cが点Bを中心として回転するとき,交点Pは2点A,Bを焦点とする楕円Eをかく。同時に,平面$${\tau}$$上に2点C,Dを焦点とする楕円E'がかかれる。楕円EとE'は点Pを接点として互いに転がり合う。


どこがどうちがうのか,ひとまず楕円の図を描いてみましょう。
楕円の場合
まず,「交叉平行四辺形ABCD」をどう描くかです。交叉平行四辺形は,平行四辺形を対角線で折り曲げた図形で,楕円の図でいうと,AB=CD,AD=BCとなります。これらの条件は,Cinderellaの作図ツールでは「コンパス」を選んで円を描くことで実現できます。次の手順で作図します。
① ABは固定なので,適当な長さの線分を描く。
② Bを中心に円を描き,円周上に点Cをとる。
③ コンパスでABの長さをとり,Cを中心に円を描く。
④ コンパスでBCの長さをとり,Aを中心に円を描き,③との交点をDとする。
⑤ CD,AD,BCを線分で結び,ADとBCの交点をPとする。
⑥ 軌跡ツールを選び,動かす点としてC,軌跡を描く点としてPを選ぶと楕円が描かれる。

楕円はひとつだけで,説明にある「平面$${\tau}$$上に2点C,Dを焦点とする楕円E'」は描かれません。これは,Cinderellaの描画面が$${\pi}$$であり,その上の軌跡が描かれるからです。$${\tau}$$の方は,点Cと同時に動くので,Cinderellaの軌跡ツールでは描かれません。
そこで,次のようにしてもうひとつの楕円も描きます。「2点C,Dを焦点とする楕円」なので,楕円ツールを使って,焦点をC,Dとし通る点としてPを選びます。

インスペクタで色を変え,線の太さもすこし太くして,点Cをドラッグすると,「楕円EとE'は点Pを接点として互いに転がり合う」様子がよくわかります。

双曲線の場合
楕円と同じように作図していきますが,図を見て,ADとCDが交わるような位置関係にします。また,手順の⑤を
⑤ CDを線分で結び,ADとBCをそれぞれ直線で結んで交点をPとする。
に変えます。
これで軌跡は双曲線になります。
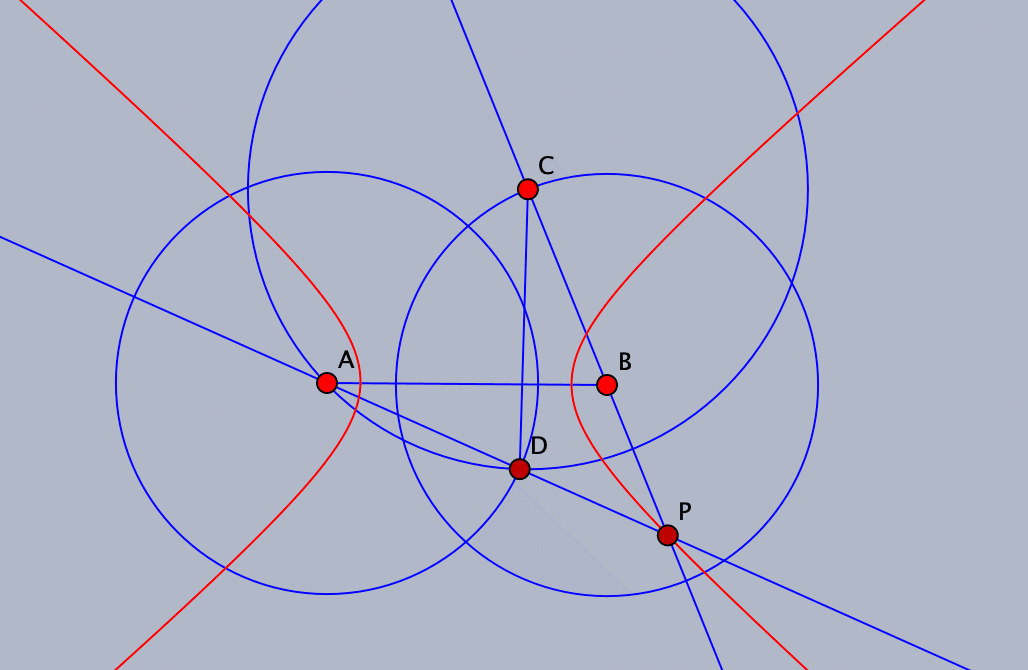
ところで,楕円の場合と双曲線の場合の違いは何でしょうか。図を見ながら位置関係を変えて描きましたが,文章での説明では全く同じです。図での違いは,ABの長さとBCの長さの違いです。今描いた双曲線の図で,Bを中心とする円の円周上をドラッグして大きくしてみましょう。すると,双曲線は楕円に変わります。
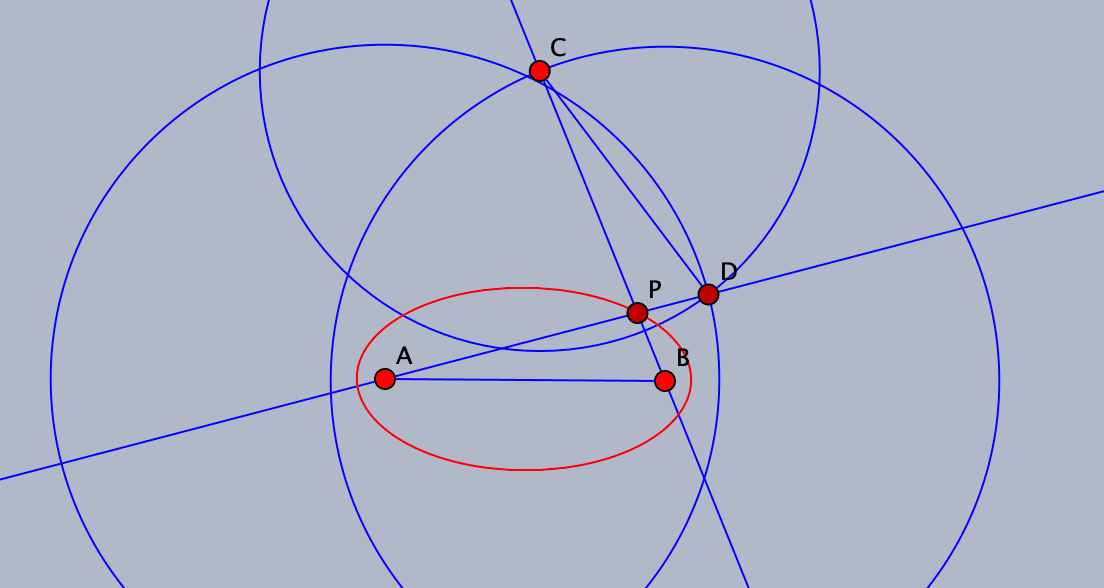
では,$${\tau}$$上の軌跡はどうなるでしょうか。双曲線の状態に戻し,双曲線ツールを選んで,焦点をC,D,通る点をPとして双曲線を描きます。先ほどと同じように,色と線の太さを変えました。

このまま,Bを中心とする円を大きくしていきますと

双曲線は楕円に変わります。
なお,点Cをドラッグしたとき,楕円の方はいかにも「転がり合う」感じがしますが,双曲線の方はそうでもありませんね。
作図器としては,棒の長さを可変にはしないので,楕円と双曲線は写真のようにことなるものとして作ります。したがって,Cinderellaで作図器を模したものも,楕円のものだけ作りました。棒の可動域には制限があるので,図の太い部分だけです。(見出し画像)
