
インドラの真珠:相似変換の反復
万華鏡や変換群では、距離・大きさを変えない変換を扱ってきました。これには理由があります。幾何変換によって距離が保存されない、つまり拡大・縮小が起こる場合、それは「カオス」としての振る舞いを起こすことになるからです。
ここで、「カオス」は一般には「渾沌」と訳されますが、数学ではもうすこし違った意味になります。
カオスにならない場合には非常にきれいな図ができます。次のリンク先を開いてみましょう。
次の図のように,2つの相似変換(回転と拡大・縮小)によって図が描かれます。右のボタン「数字を表示」や左の文字が表示されない場合は再読み込みしてください。
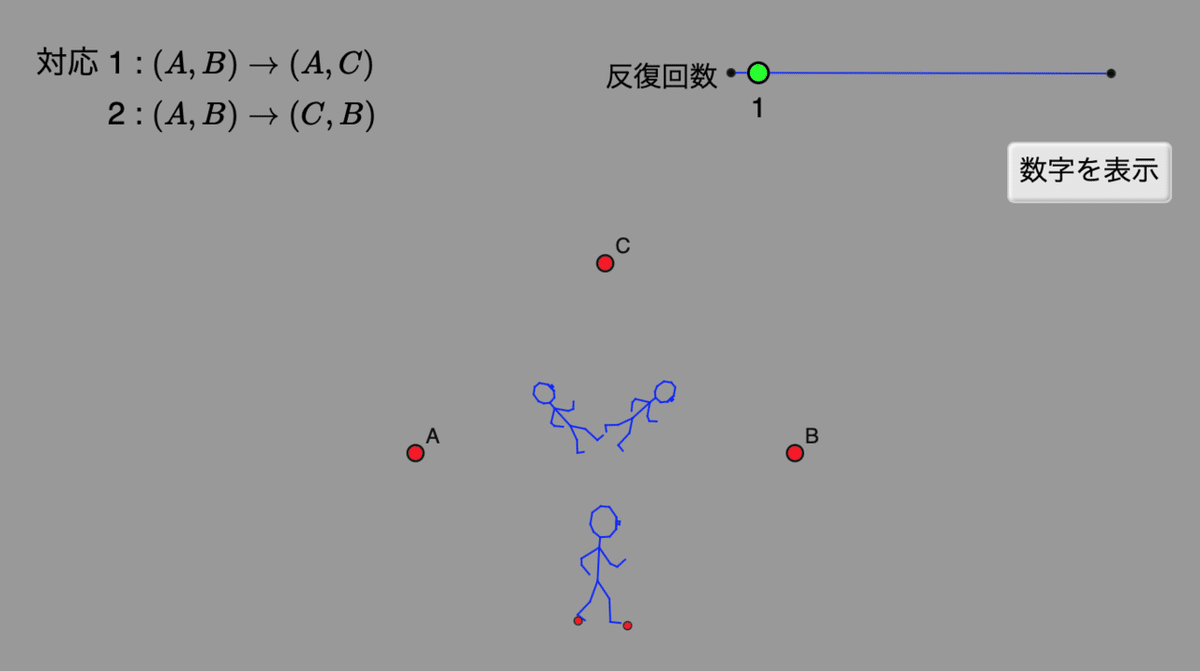
変換は3つの点A,B,Cによって定義されます。
第1の変換は、線分ABを線分ACに写す、という変換で定義されます。
第2の変換は、線分ABを線分CBに写す、という変換で定義されます。
この2つの変換を繰り返します。右上の白いスライダーで、反復回数を変えることができます。はじめは1回変換を実行したところです。 反復回数を増やすと次のようになっていきます。

点A,B,Cの位置を変えると、変換の定義が変わります。

2つの変換のどちらでできた図かを明示するために、数字を表示してわかりやすくすることができます。「数字を表示」ボタンを押してみましょう。
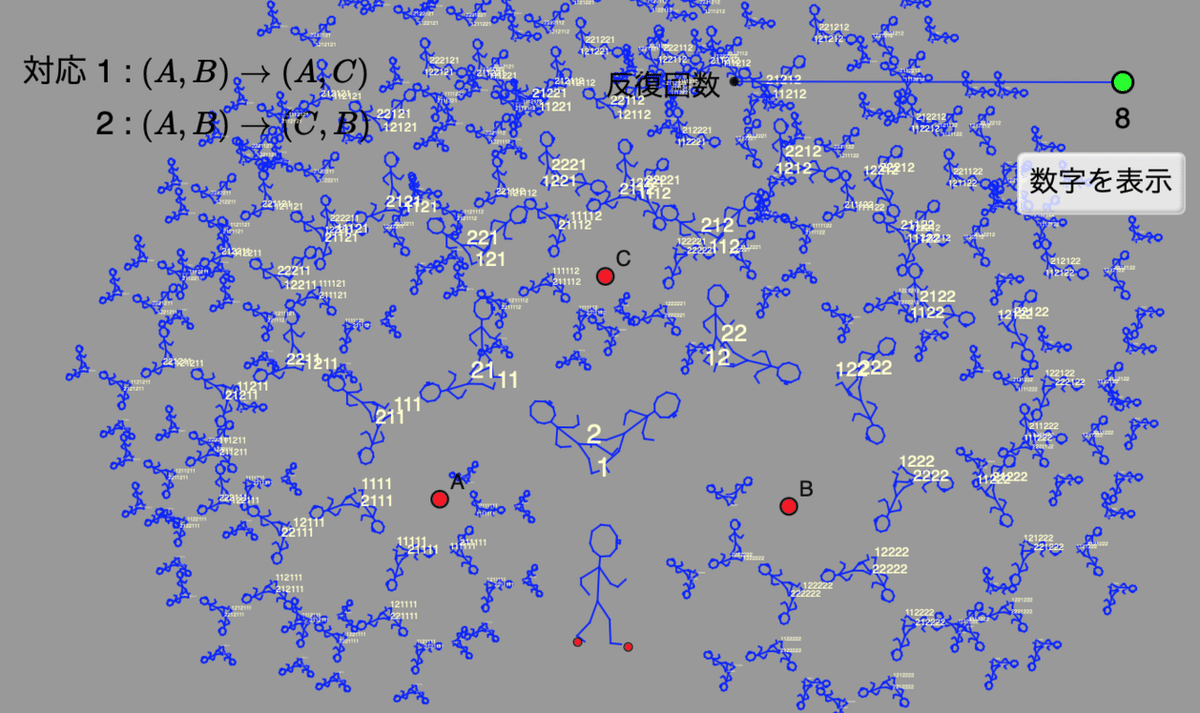
たとえば、変換1だけを 1,11,111,・・・と追っていくと、点Aに螺旋状に近づいていきます。 変換2だけを 2,22,222, ・・・と追っていくと、点Bに螺旋状に近づいていきます。 また、スティックラー博士の像は次第に小さくなっていきます。
それぞれの変換を使ってできる像は一つの集合を作ります。これを極限集合と呼びます。ちょっとわかりにくいですね。 「極限集合」については,「ショットキー円」のところでもう一度説明します。
反復回数を最大(8回)にし、スティックラー博士の足をドラッグして、スティックラー博士をいろいろな場所に動かしてみましょう。どんなことがわかりますか?

これは相似変換ですが,メビウス変換の反復によってできる極限集合はインドラの真珠の主要テーマの一つです。
→インドラの真珠:目次 に戻る
