
インドラの真珠:アポロニウス・パッキング
ショットキー・ダンスで,4つの円のうち、ひとつを半径無限大すなわち直線とし、残り3つの円を対称形に配置してできる極限集合が「アポロニウス・パッキング」です(見出し画像)。オリジナルのMatheiVitalでは、「おばあちゃんのレシピ」による1つの場合として掲載されていますが,ここではまずショットキー・ダンスのバリエーションとして作ります。
リンク先を開くと次の画面になります。
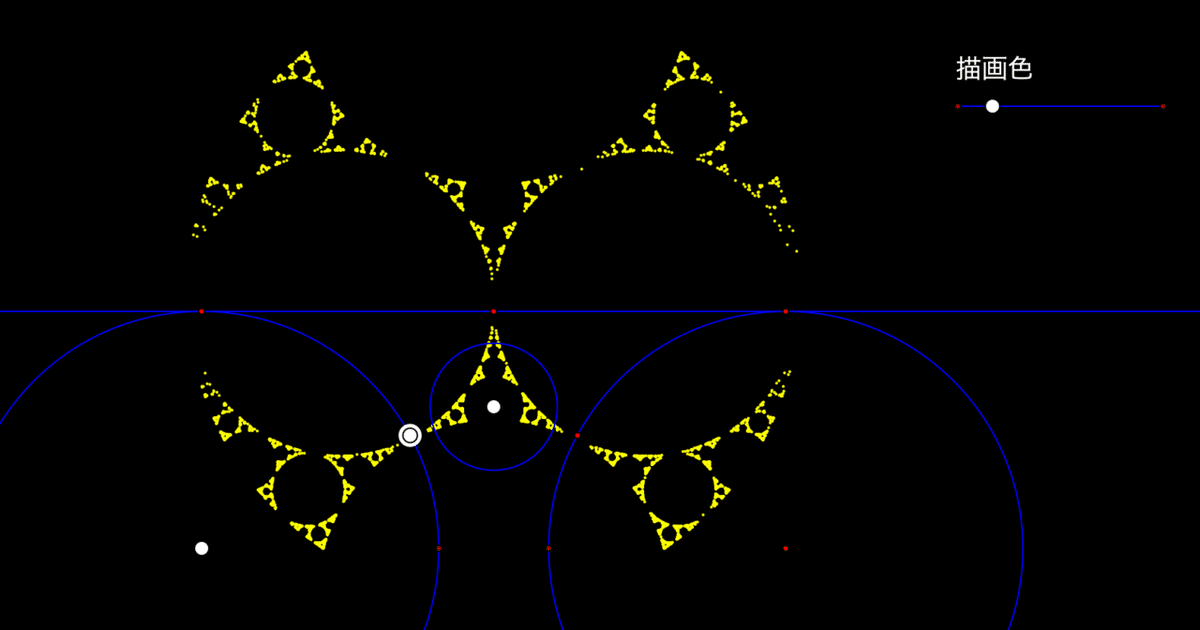
直線と3つの円は接していません。「インドラの真珠(D.マンフォード,C.シリーズ,D.マンフォード 小森洋平訳 日本評論社)」の191ページにある図をやってみたいのです。次の図です。

この図になるように,白い点を動かして円を配置していくと次のようになりますのでやってみてください。
大円どうしは接しておらず,小円と直線も接していない状態

小円と直線は接しているが大円どうしは接していない状態。

それぞれお互いに接している状態。これがアポロニウス・パッキング。

「インドラの真珠」の190ページには,ショットキー・ダンスの続きのような図があります。Mathe Vital にはありませんでしたが,これも作ってみました。
リンク先を開き,白い点を動かしてみましょう。

本に掲載の図と比べると,解像度が甘い感じがします。精細さが足りないと行ってもよいでしょうか。しかし,CindyScriptとCindyJSはこのくらいが限度。Web上で動かすのでなければ,Cinderellaのツールでプログラムを書かなくてもできますので,このあと示しましょう。
見出し画像の図は,CindyJSに加えて,CindyGLも使って描いたものです。これについては,最後の節「おばあちゃんのレシピ」で説明しますが,次のリンク先をクリックしてみましょう。
リンク先を開くとつぎの画面になります。今度は描画色のスライダだけがあります。描画レベルのボタンはなく,つねにこの解像度で表示されます。

=================
ここから先は,プログラミングをせずに,Cinderellaの作図機能だけでアポロニウス・パッキングを作る手順を説明します。
4つの円のうち、ひとつを半径無限大すなわち直線とし、残り3つの円を対称形に配置してできる極限集合が「アポロニウス・パッキング」です。下図、直線ABとC,D,Fを中心とする円でメビウス変換を定義します。

では、作図してみましょう。画面下の磁石ツール(グリッドにスナップする)で,方眼を表示しておくとよいでしょう。スナップ機能が邪魔なら磁石ツールだけを解除します。
まず、直線ABと2つの大円を描きます。ABの中点Eをとり,Eを通る垂線を引き,その上に適当に点Fをとって,Fを中心とする円を描きます。

2つの大円の中心を結び、円との交点G,Hをとります。小円は位置と半径を調節して大円と接するようにし、接点を点K,Lとします。ここで、K,Lは点を加えるモードでとります。小円と大円が同時にハイライトする点に置きますが、実際には交点ではなく大円上の点です。このことがあとで意味を持ちます。

大円どうしで次の図のようにメビウス変換を定義します。
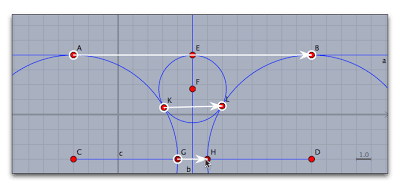
小円と直線で次の図のようにメビウス変換を定義します。2つめは E->Eです。

2つのメビウス変換の逆変換を作り、この4つの変換で反復関数系を定義します。

大円、小円の位置と半径を調節して、3つの円が接するようにすればでき上がりです。対称形の図ができます。

さて、小円と大円の接点は実際には接点ではなく自由点でした。ですから、ドラッグして動かすことができます。少し上に動かしたのが次の図です。

この他、明るい赤で表示されている点は動かすことができるのでさまざまなバリエーションが楽しめます。
さて,ここまでで気付かれた方もいるでしょうが,実はFを中心とする小円はなくてもこのような図は描けます。円2つと直線1つです。ただし,きれいに閉じた円するには小円があったほうがよいでしょう。やってみましょう。
背景を黒にして、極限集合を黄色とし、ラベルは非表示にして点も小さくしたのが下図です。

→次節:おばあちゃんのレシピ
→インドラの真珠:目次 に戻る
