
PythonでL-Systemsを作る(4)コマンドを追加する
リンデンマイヤーの L-Systems で使っているコマンドは,LOGOのタートルグラフィクスとはすこし違う。前進には A,B,F の3種類があり,何もしないというコマンドもあるのだ。
if command == "A" or command == "B" or command == "F":
state = forward(state)
なぜそのようなコマンドがあるかを簡単に説明しておく。(「簡単」というのは原理が簡単なのではなく,細かいことはさておいて,という意味)
リンデンマイヤーの The Algorithmic Beauty of Plants は,Algorithmic Botany のページから PDF を閲覧することができる。
直接PDFにいくならこちら。
Edge-rewriting L-systems
この中で,リンデンマイヤーは,コッホ曲線の拡張として,Edge-rewriting L-systems というのを導入している。ドラゴン曲線がその例。

「フラクタルCGコレクション」(渕上季代絵:サイエンス社)では,これを「ジェネレータを2つ準備しますが,第2のジェネレータは第1のジェネレータを逆さにしたものとします。」と説明している。
リンデンマイヤーは「"左 "と "右 "の2種類のエッジを仮定すると、多くの面白い曲線が得られる。」と書いている。この「「"左 "と "右 "」はあとでまた説明するが,とりあえず,このドラゴン曲線で,2つのジェネレータでどのように置き換えが行われていくかを見ておこう。イニシエータとジェネレータは次のようになっている。
initiator = "A"
generator = {"A":"A+B+","B":"-A-B"}
Aを青,Bを赤で示す。はじめはイニシエータの青の線が1本である。

この作り方は,「フラクタルCGコレクション」のものとは少し異なるが,結果としては同じものができる。
次に,"右"と"左" について。空間充填曲線との関係で例示されている。

線に,進行方向(左から右へ)から見て,右または左にマークがついている。このマークのあるほうの正方形を,線と一緒に書いていく。
左側の Fl→FlFl+Fr+Fr-Fl-Fl+Fr+FrFl-Fr-FlFlFr+ Fl-Fr-FlFl-Fr+FlFr+Fr+Fl-Fl-FrFr+ で,正方形が5×5に分割され,埋め尽くされている(充填) 右側も同様。
この2つのジェネレータを用いるとペアノ曲線(ゴスペル曲線)が描かれる。FlをA, Fr をBとしてやってみよう。イニシエータは -B とする。1回置き換えを行うと上の図の右側になる。

これを無限回繰り返していけば平面が線で覆われるというわけだ。(平面充填)
回転角を60°にした曲線もある。
initiator = "A"
generator = {"A":"A+B++B-A--AA-B+", "B":"-A+BB++B+A--A-B"}

Node rewriting
L-Systems にはもう一つ,Node rewriting というものがある。たとえば,ヒルベルト曲線の例。
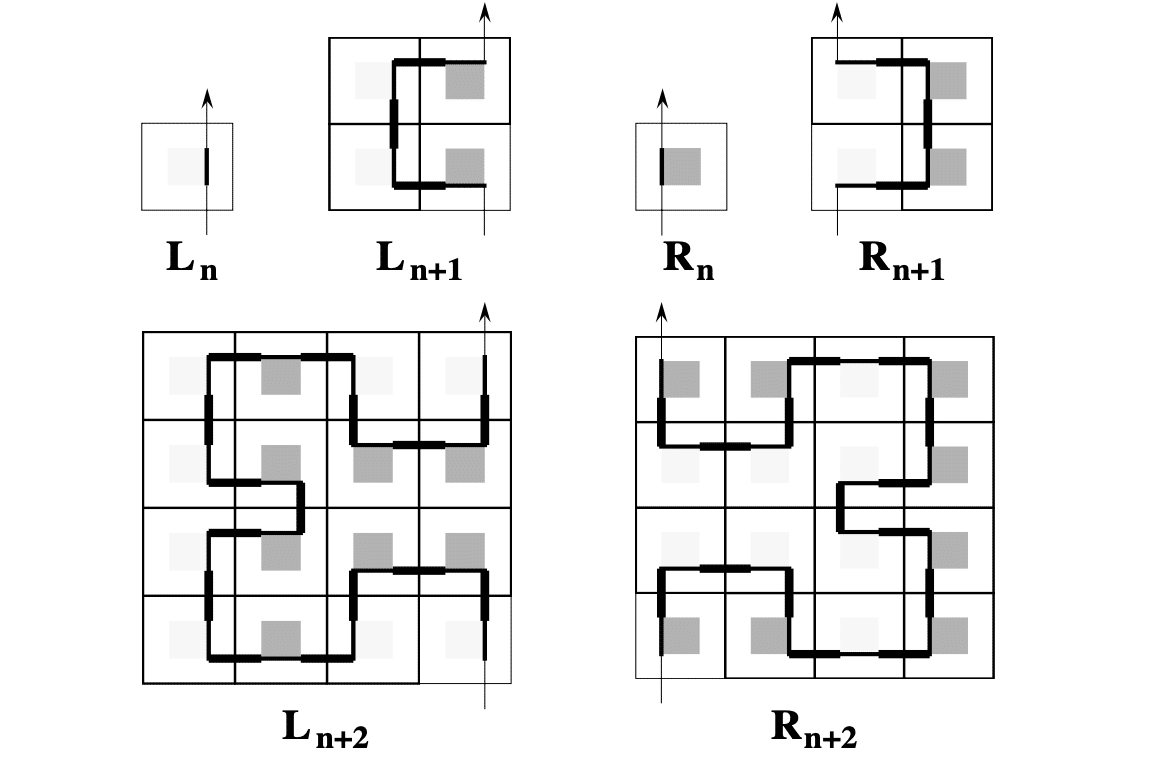
Ln は進行方向の左側に正方形があり,Rnは右側に正方形がある方向ベクトルと考えよう。ここは少しややこしい。亀になったつもりで考える。
まず,Ln+1 の進みかた。右下から上向きに入ってきた。
ここで左を向く(+)。このとき,Rn を左に倒すので +Rn と表す。1歩進む F
次に右を向く。このとき,Lnを右に倒すので -Ln と表す。(ここが大切。亀目線で考える)1歩進む F。次は Lnは倒さなくてよいので単に Lnで,右を向く -。
1歩進む F。Rnは倒さなくてよいので単にRn。最後に左を向く +。
以上を続けると
Ln+1 = +RnF−LnFLn−FRn+
となる。同様に,右側は
Rn+1 = −LnF+RnFRn+FLn−
イニシエータを L とし,上の関係をジェネレータとすると,次のように図ができる。(図は repeat =5 )
このとき,L,R では何もしない。
angle = 90 / 180 * np.pi
initiator = "L"
generator = {"L":"+RF-LFL-FR+", "R":"-LF+RFR+FL-"}

Edge-rewriting と Node rewriting の関係
Edge-rewriting と Node rewriting は別なものではなく,表現方法の違いといえる。たとえば,ドラゴン曲線は,
Edge-rewriting では
initiator = "A"
generator = {"A":"A+B+", "B":"-A-B"}
と表したが,リンデンマイヤーの本では,もともと
initiator = "Fl"
generator = {"Fl":"Fl+Fr+", "Fr":"-Fl-Fr"}
と表されている。小文字のエルとアールだ。
これを書き換えると,Node rewriting では
initiator = "FL"
generator = {"L":"L+RF+", "R":"-FL-R"}
となる。詳しくはリンデンマイヤーの本を参照されたい。
(といって,これを自分で考えろというのは難しい)
2つのシェルピンスキーギャスケット
フラクタルで有名なものにシェルピンスキーギャスケットがある。リンデンマイヤーの本に載っているのは,Edge-rewriting で描いた次の図。
angle = 60 / 180 * np.pi
initiator = "B"
generator = {"A":"B+A+B", "B":"A-B-A"}
repeat = 6

山口大学のテキストには次の例が載っている。(ずいぶん前のことで,もうWeb上には残っていないようだ)
state = [[4, 6], -np.pi/3] # 亀の初期状態 出発点とはじめの向き
angle = 120 / 180 * np.pi
initiator = "R-F-F"
generator = {"F":"FF", "R":"F-R+R+R-F"}

==========================================
以上で,よくあるフラクタル図形についてはひととおりやってみた。
次回は,いよいよ植物の成長システムを作る。
→(5) 植物の成長システム
