
Cinderellaで数学:いろいろな曲線:極線による包絡線と円錐曲線作図器
「曲線の事典」(礒田正美他編著:共立出版 2009)に掲載されている,極線による包絡線で円錐曲線を作図するものです。
極線とは
まず,「極線」とは何かについて調べておきましょう。「曲線の事典」には次のように書かれています。
円と点Pがある。このとき,点Pを通る円の接線を2本引くことができる。接線と円との交点を通る直線をその円に関する点Pの極線といい,Pをその極線の極という。
Web上を検索してもだいたい似たようなものですが,円ではなく楕円などの二次曲線でも同様で,より一般的な定義はコトバンクに書かれています。
つまり,「ある点から二次曲線に引いた2本の接線の接点を通る直線が極線」,と考えてよいでしょう。Cinderellaではこの形で極線を作図するツールがあります。「点の極線を加える」「直線の極点を加える」の2つです。いずれも二次曲線と点または直線を指定します。
次の図は楕円の極線です。左が点が楕円の外側にあるときで,極線と楕円の交点と点Lを結べば接線が引けます。右は点が楕円上にあるときで,極線は接線になります。

次の図は放物線と極線です。

極線による包絡線
「曲線の事典」の記述です。
5点OAPBQはポースリエの反転器(OA=OB, PA=PB=QA=QB)を形成しており,点C,Dは点A,Bについてそれぞれ点Pと対称な点とする。点Oは平面に固定されており,点Pは中心M,半径rの円$${\gamma}$$上を動く。このとき,中心O,半径$${\sqrt{\rm{OA^2-AP^2}}}$$の円に関して,点Pを極とする極線 CDによる包絡線は円錐曲線になり,半径rとOMの大小関係によって分類される。

この説明文には疑問があります。「中心O,半径$${\sqrt{\rm{OA^2-AP^2}}}$$の円」が,図にありません。したがって,CDがその円の極線になるかどうかが不明なのです。まずはこれを確かめましょう。
その前に,動かせるものとそうでないものをはっきりさせておく必要があります。点Oと点Mは固定点ですが動かすことはできます。AとBはPA=PBとなる点ですが,長さPAは一定です。すなわち,動点Pが動いたとき,PAの長さは変化しないようにします。このことは説明文に書かれていませんが,放物線の作図器の写真(後出)を見るとわかります。
Cinderellaで,上の図に合わせて図を描きます。なお,点をとるたびにインスペクタで点の名称を変えていきます。
① 固定点O,Mをとり,それぞれを中心とする円を描く。
② Mを中心とする円の円周上に動点Pをとる。
③ Pを中心とする円を描き,Oを中心とする円との交点をA,Bとする。
これで,OA=OB,PA=PB となる。
④ 鏡映ツールを使って,Aに関するPの対称点C,Bに関するPの対称点Dをとる。
点Qは今は不要なのでとっていません。それぞれ線分で結んだのが次の図です。
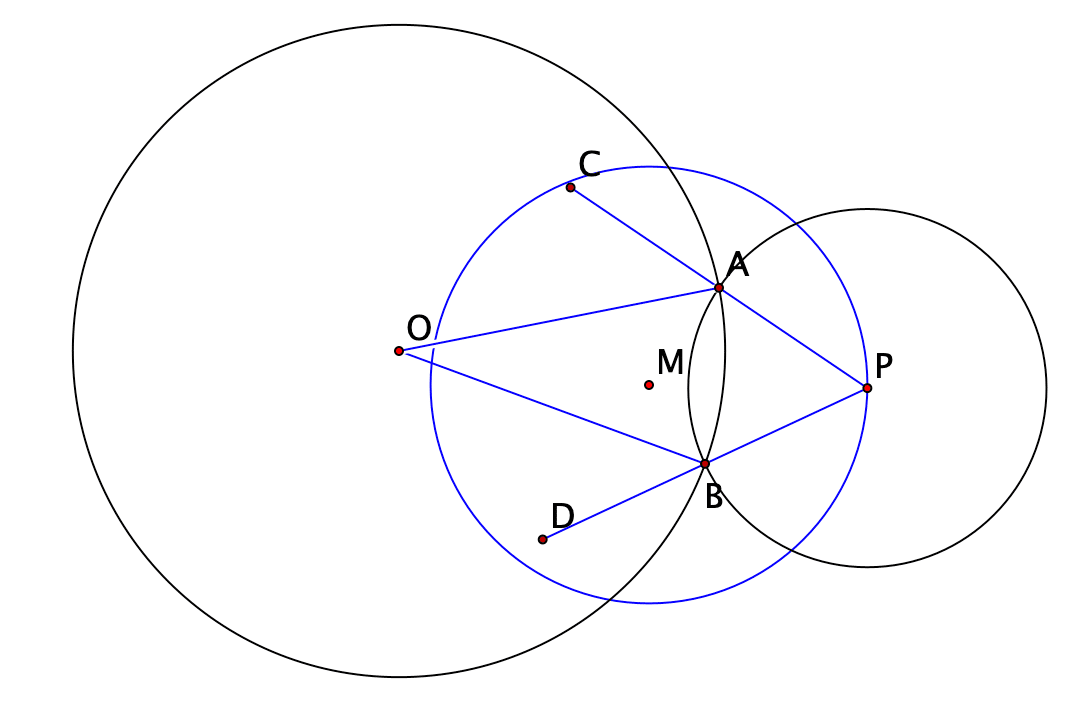
次に,元の図にはない,「中心O,半径$${\sqrt{\rm{OA^2-AP^2}}}$$の円」を描き,点Pの極線がCDになるかどうかを確かめます。この円を描くためには三平方の定理を使います。OAを直径とする円を描き,Aを中心とする半径APの円も描いて交点Fを求めると,$${\rm{OF}=\sqrt{\rm{OA^2-AP^2}}}$$となります。次図で緑の線が,この作図に要した線です。
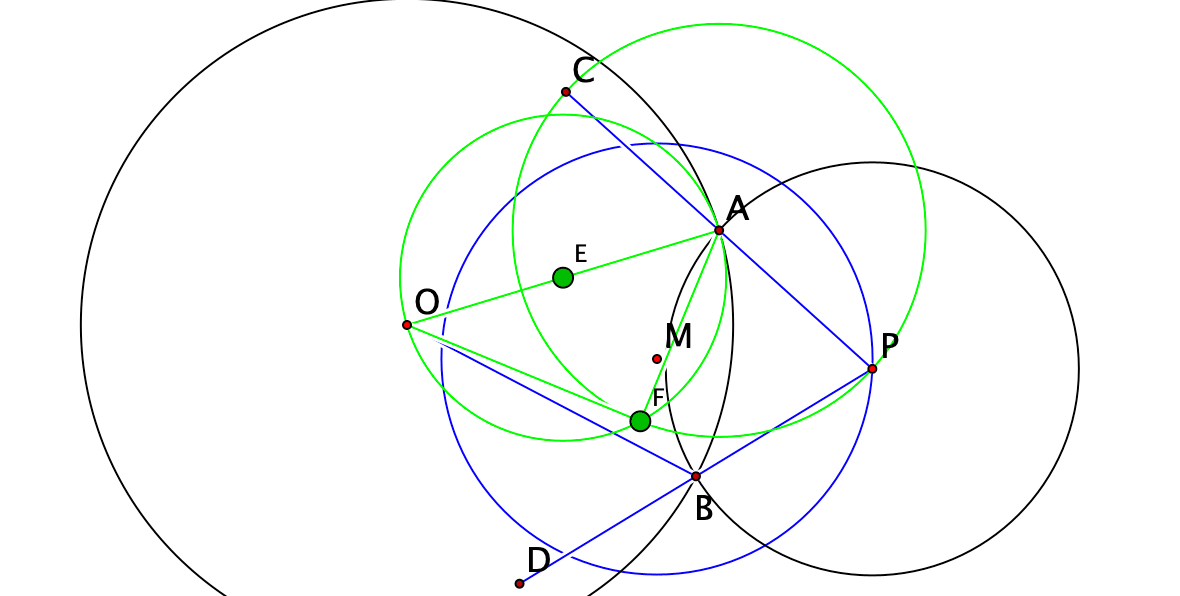
中心O,OFを半径とする円を描いて,「点の極線を加える」ツールで,今の円と点Pを選択すると極線が描かれますが,ちょうどC,Dを通りました。

放物線
Mを中心とする円の半径がOMのとき、極線CDによる包絡線は放物線になります。

CDが極線であることを確かめるために使った点は消して,(直線CDは残します)インスペクタの特別な表示方法でCDの「足跡を描く」にチェックを入れます。Mを中心とする円の半径がOMになるようにして,点Pをドラッグすると,包絡線が放物線になるのがわかります。

OAやAPの長さを決める黒の円をドラッグして長さを変えると,放物線も変わります。
楕円
Mを中心とする円の半径がOMより大きいとき、極線CDによる包絡線は放物線になります。

作図器の形状は放物線のものとは異なりますが,Cinderellaの作図上では同じものが使えます。点Mの位置を移動するだけです。

双曲線
Mを中心とする円の半径がOMより小さいとき、極線CDによる包絡線は放物線になります。

作図器の形状は放物線のものとは異なりますが,Cinderellaの作図上では同じものが使えます。また,この右図では点Qが表示されています。放物線・楕円の場合も点Qは,包絡線には直接はかかわらず,包絡線が円錐曲線であることを示すために使われており,直線CDが接線であることの説明にも使われます。(引用は略)

各作図器は,中心O,半径$${\sqrt{\rm{OA^2-AP^2}}}$$の円の極線を描くために,棒PC,PDを作って動かすようになっています。放物線の作図器を模したものを次のように作ってみました。(見出し画像)
作図ツールによる,極線と二次曲線
ところで,始めに調べたように,作図器による直線CDは,作図ツールで描いた極線と一致しました。それならば,始めから2つの円と極線を描くだけで二次曲線が描けるのではないでしょうか。
Cinderellaで2つの円を描き,一方の円周上に点を取って,他方の円に関する極線を描きます。

点Cを動かして,極線の包絡線を調べましょう。やってみると,2円の大きさ,位置関係によって,放物線・楕円・双曲線を描くことができます。



Cinderellaでは「点の極線を加える」ツールがあるのでこれを使いましたが,このツールがなくても接線を描いて接点を結べば極線が描けるので,どんな作図ツールでも描くことができるでしょう。
