インドラの真珠：首飾りその１

2022年3月26日 09:01

　前の例の２直線は、円の半径を無限大と考えたものでした。
今度は無限大ではないけれど、かなり大きな円とし、１点で接するのものを考えます。さらに制限をつけて、その２円の半径は同じであるとし、あとの２円もこれらに接するものとします。全体が対称形になるように配置します。

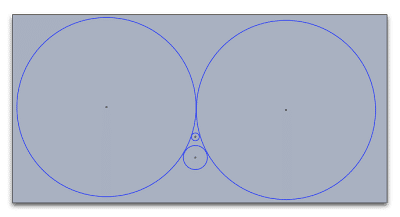
実際には全体をこれよりずっと大きくします。

リンク先を開くとつぎの画面になります。

緑の円は首飾りの輪郭で，青い円がいままでやっていたメビウス変換を定義するための円です。この作図方法については後述します。
ショットキー・ダンスでやっていた４つの円を，この配置にすると，極限集合が首飾りのようになるのです。
右上のスライダで描画色を変えてみましょう。

白い点をドラッグすると首飾りの幅を変えることができます。このとき，青い小さな２つの円が接するようにするのが要領です。

前の節でもそうでしたが，Web上で動かすためにプログラムを書いたものより，Cinderellaの作図ツールで作図したものの方が精細な図になります。見出し画像がその図ですが，以下で，その方法を示します。

======================

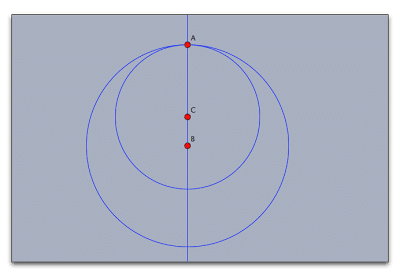
まず、縦線ABを取り， Bを中心に半径ABの円を描きます。
直線AB上の適当な点Ｃをとり、Cを中心に半径CAの円をとります。
これが首飾りの輪郭になります。Cの位置で太さが変わります。

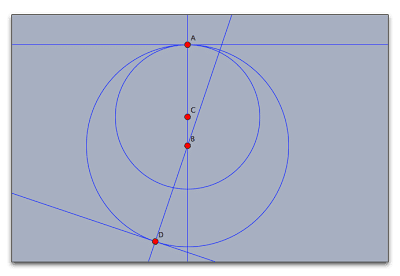
外側の円の下部で適当な場所に点Dをとり、直線BDを引きます。垂線ツールを用いて、点Aを通るABの垂線、点Dを通るBDの垂線を引きます。この２本の垂線の交点をとれば、それがA,Dを接点とする大きな円の中心になります。

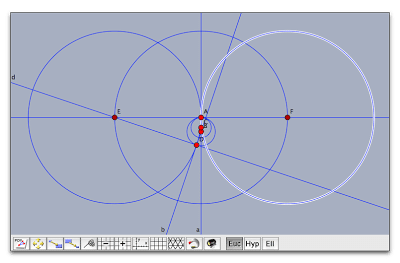
２本の垂線の交点Eは描画面をはみ出してしまいますので、平行移動ツールや縮小ツールを用いて、点Eが現れるようにします。縮小したら、あとから拡大ツールで戻します。

かなり縮小しました。点Eを中心に半径AEの円を描き、Aを中心に同じ半径の円を描き、Eの反対側に交点FをとってFを中心とする円を描きます。

拡大ツールで元の大きさに戻します。首飾りの輪郭としてとった小さい方の円と、大円との交点を取ります。点を加えるツールを用い、２つの円がハイライトする点でマウスボタンを離します。下図、G,Hです。
CHを結ぶ直線を引き、Hで垂線を引きます。この垂線は右側の大円の中心Ｆを通ります。この垂線と、直線ABの交点を取ります。Ｋです。
ＤにおけるBDの垂線（すでに描いてあります）と直線ABの交点をとります。Ｌです。首飾りの輪郭としてとった大きい方の円と、右側の大円との交点を取ります。Dの対称点となります。Mになります。