自己平方フラクタル(1) マンデルブロ集合

　複素数平面上で「自己平方フラクタル」を考えます。
　自己平方フラクタルとは，複素数平面上の各点について，次のような2次関数を使って収束・発散を調べ，作図する方法です。（フラクタルＣＧコレクション：渕上季代絵：サイエンス社 48ページ：以下，「この本」）

　　　$${f(z)=z^2+ c}$$

$${z,c}$$ は複素数です。複素数平面上の点$${z_0}$$ に対し，漸化式 $${z_{n+1}=f(z_n)}$$ を適用して計算を繰り返し，絶対値がある値（この本では「ある値」としか書いてありませんが，ここでは「境界値」と呼ぶことにします）を超えれば発散，そうでなければ収束とします。また，繰り返す回数も無限回というのは実際にはできないのである回数に制限します。「自己平方フラクタル」はマンデルブロの命名のようで，cが0でないときすべての図形はフラクタル構造をもっているだろう，と予測しています。（この本 48ページ，および「フラクタル幾何学（上）：マンデルブロ著　広中平祐監訳　ちくま学芸文庫　402ページ」）

　ここで，$${z_0}$$ と $${c}$$ のどちらを固定するかによって2通りの場合があります。初期値 $${z_0}$$ を 0 に固定し ，c を複素数平面上の各点とし，境界値を2として，収束するならば黒，発散するならば白で表した図形がよく見るモノクロのマンデルブロ集合です。黒と白ではなく，境界値を超える回数で色分けすると美しい図が現れます。

その原理を見てみましょう。

マンデルブロ集合の原理

リンク先を開くと次の画面になります。

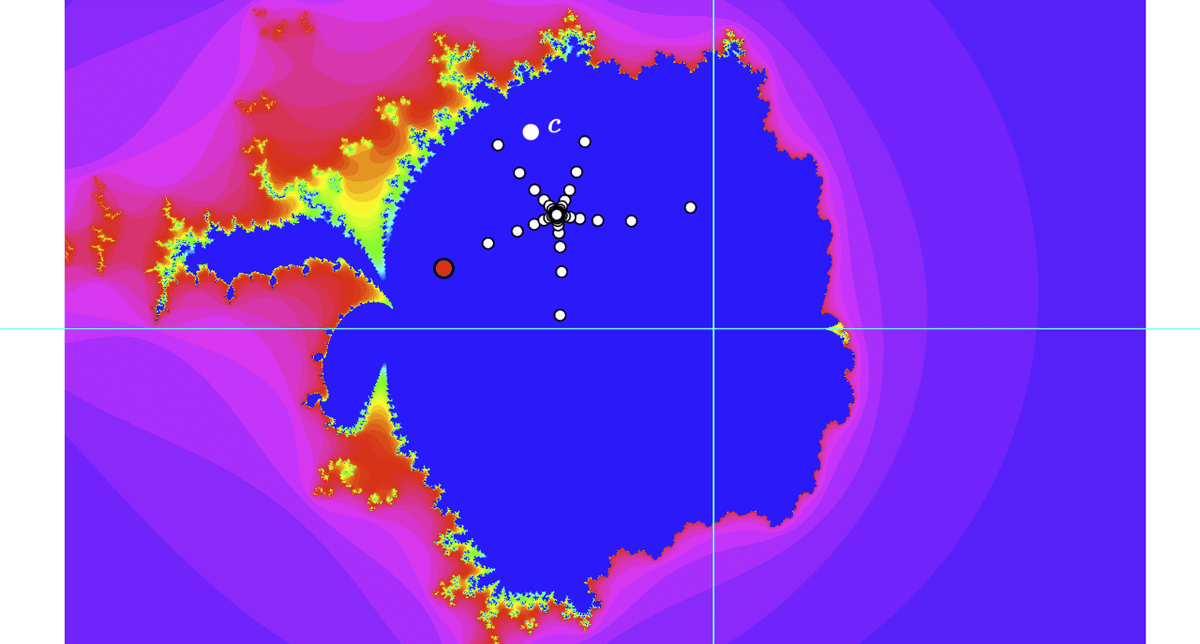
赤い点が原点 $${z_0=0}$$，白い大きな点が c です。白い小さな点は，$${z_{n+1}=f(z_n}$$で変換していくときの点を表します。50個まで表示していますが，発散すれば画面の外になりますし，ある点に収束すれば重なって見かけは少しになります。このはじめの図では c の右下に収束します。
白い点c をドラッグしてみましょう。
中の青いエリアを湖にたとえると，陸地にあがったときに発散していくのがわかります。描画範囲は横が -1.5  から 1 までなのですが，その範囲外に白い点が出ています。

原点を中心とする半径２の円の中に入るかどうかで収束・発散としているわけですが，何個まで入るかで色分けすると，このようなカラーの画像になります。

では，このツールで，マンデルブロ集合で通常はやらないことをやってみましょう。
赤い点が原点です。すなわち，初期値 $${z_0}$$ です。念のため，少し値を追うと，$${z_0=0}$$ のとき，$${f(z)=z^2+ c}$$　で次々に点を求めていくと
　$${f(0)=c}$$ , $${f(c)=c^2+c}$$ , $${f(c^2+c)=(c^2+c)^2+c}$$ , ・・・
となっていきます。
この初期値を変えたらどうなるでしょうか。
赤い点をドラッグすると，初期値を原点以外にすることができます。
左に動かしていくと，湖の左にあった岬が２つに割れ・・・

左上に持っていくと上下の対称性が崩れます。

ちょっと面白い実験をやってみました。

　では，$${f(z)=z^2+ c}$$ で，初期値 $${z_0}$$ を 0 に固定し ，c を複素数平面上の点とするのではなく，cを固定し，初期値の$${z_0}$$ を複素数平面上の点にとったらどうなるでしょうか。それを次にやってみましょう。

→複素数平面とフラクタル　に戻る