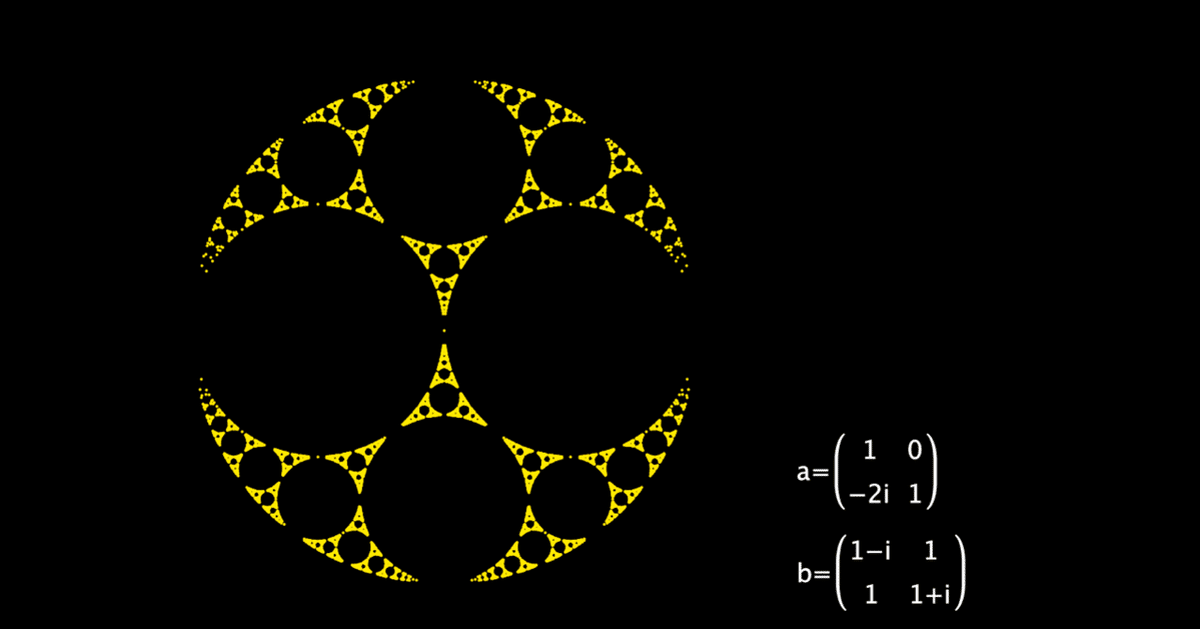
インドラの真珠:おばあちゃんのレシピ
ここまで、2つの円で定義されるメビウス変換を2組使って反復関数系を作りその極限集合を見てきました。これに対し、「おばあちゃんのレシピ」では、2つのパラメータだけでメビウス変換を定義します。メビウス変換は2行2列の行列で表されますので、2つのパラメータ $${t_a,\ t_b}$$ を使って,次のようにこの行列を定義するのです。(インドラの真珠 マンフォード他著 218ページ : 面倒な人は式は眺めるだけで結構)
(1) 任意の複素数 $${t_a}$$ と $${t_b}$$ を選ぶ。
(2) 2次方程式 $${x^2-t_a t_b x+t_a^2 + t_b^2=0}$$ の解$${x}$$ を選んで $${t_{ab}=x}$$ とおく。
(3) 次のように $${z_0}$$ を定義する。
$${z_0=\dfrac{(t_{ab}-2)t_b}{t_b t_{ab}-2 t_a+2 i t_{ab}}}$$
(4) 生成元の行列を計算する。(行列の表示ができないようなので画像です)

(2) では解が次のように2つ出ます。
$${t_{ab}=\dfrac{t_a t_b \pm \sqrt{(t_a t_b)^2-4(t_a^2+t_b^2)}}{2}}$$
そのどちらを選ぶかですが,マイナスの方を選んだのがこのあとに示すもので,アポロニウス・パッキングが作れます。
リンク先を開くと次の画面になります。前節でやったアポロニウス・パッキングですね。

パラメータ $${t_a,\ t_b}$$ (以下,画面に合わせて ta, tb と記述)は両方とも 2 で,画面上で重なっています。この白い点を動かすと値が変わります。画面は複素数平面(複素平面)で,アポロニウス・パッキングの中心が原点0です。また,このとき,メビウス変換を定義する行列は左下のものになります。i * 2 は$${2i}$$ ですが,CindyScriptで表示されるそのままにしています。もちろん,表示を通常の形にすることは可能ですが,たいした問題ではないでしょう。
スライダで色を変えて「高精細ボタン」を押してみましょう。

なお,ボタンを押した時だけ,ちょっと待つと表示が変わります。その後,画面上でマウスカーソルを動かすともとに戻ります。高精細表示は時間がかかるため,そのままではスライダなどの動きが鈍くなるのでこのようにしています。
今,ta と tb を定義する点は2つ重なっています。これをドラッグしてみましょう。
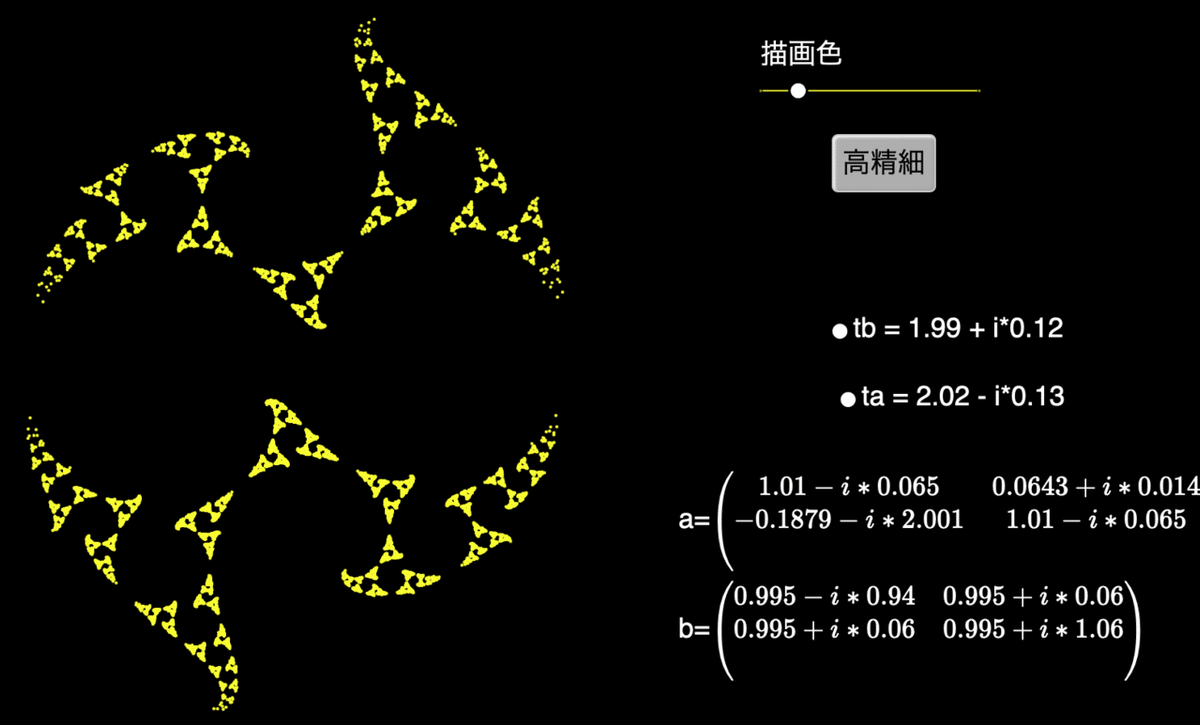
なかなか興味深い図になると思いきや,あっというまにカオス状態に陥ることもあります。

現在,オリジナルのMatheVital のページではこれらをWeb上で動かすことはできませんが,CindyJSのギャラリーには,CindyGLを使い,別の方法で表示したものがあります。
左右2つの図のうち,左がアポロニウス・パッキングで,中央の点をドラッグすると図を変化させることができます。
オリジナルのMatheVital ではここまでですが,もう少し進めてみましょう。
解 $${t_{ab}=\dfrac{t_a t_b \pm \sqrt{(t_a t_b)^2-4(t_a^2+t_b^2)}}{2}}$$ のうち,プラスの方を選んだものを作ってみました。

マイナスのときとは違ったパターンで楽しめます。
次の節では,さらに「インドラの真珠」の本にしたがって,いくつか実験をしてみます。
→次節:パラメータで遊ぼう
