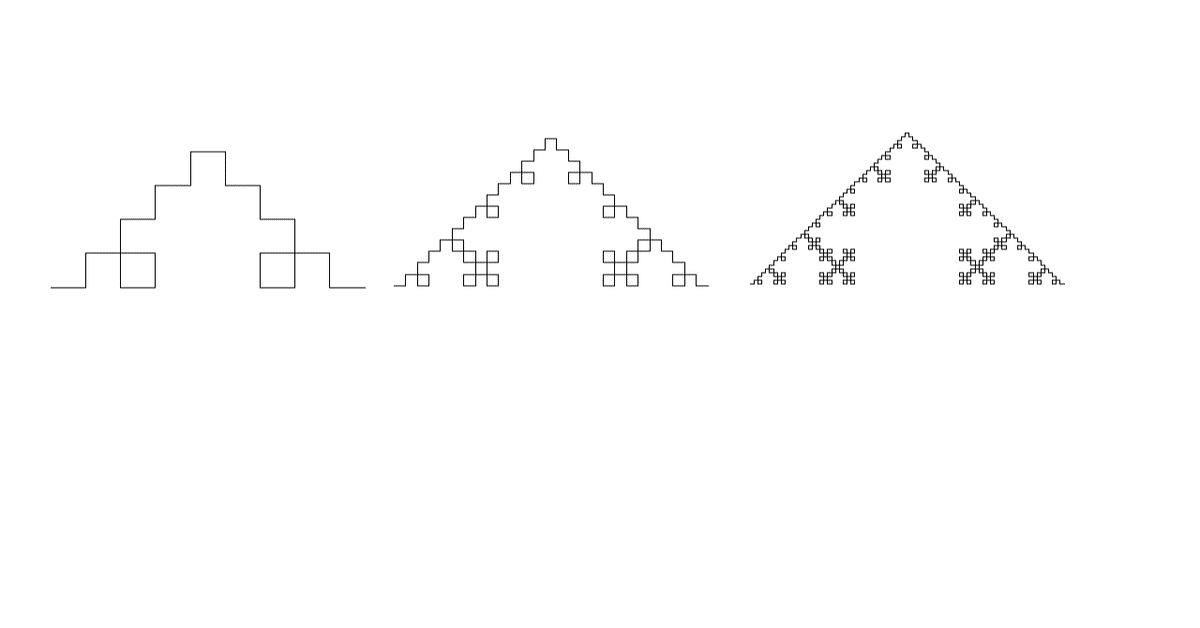
PythonでL-Systemsを作る(3) タートルグラフィクスシステムを作る
Pythonにはタートルグラフィクスのモジュール turtle がある。しかし,これを使わず,L-Systems向けのタートルグラフィクスのシステムを作る。
Tkinter ではなく matplotlib をベースにする。用意するコマンドは,最低限次の4つでよい。
F 前へ描画しながら進む:実際には forward() として関数を作る
f 描画しないで前へ進む
+ 反時計回り(左:正の角)に向きを変える
- 時計回り(右:負の角)に向きを変える
これらのコマンドを実行する関数を定義していく。
PythonでL-Systemsを作る(1) に書いたように,描画面上の絶対的な座標系と,亀にとっての座標系(相対座標系)を考える。亀はいつも自分がいるところから向いている方向にどれだけ進むのかを考える。「向きを変える」命令が出たら向きを変えるが,進むのはいつも「前」だ。L-Systems では後ろには進まない。後ろに進む必要が出れば180度向きを変えて前に進む。
そこで,亀のいる位置と向いている方向の2つを「亀の状態」として,リストで表す。この [位置, 向いている方向] は絶対座標系で考えたものだ。これを state としよう。亀が動くたびにこの state をその時の状態にしていく。つまり,コマンドを実行したらその戻り値として state を戻すようにする。
# 描画して進む
def forward(state):
th = state[1]
x1 = state[0][0]
y1 = state[0][1]
x2 = x1 + distance*np.cos(th)
y2 = y1 + distance*np.sin(th)
plt.plot([x1, x2], [y1, y2], lw=1, color=drawcolor)
return [[x2, y2],th]
# 描画せずに移動する
def translate(state):
th = state[1]
x = state[0][0] + distance*np.cos(th)
y = state[0][1] + distance*np.sin(th)
return [[x, y],th]
# 向きを変える direc 1/-1 左 / 右
def rotate(direc, state):
th = state[1]
th = th + direc*angle
return [state[0], th]
# 亀を命令に従って動かす
def turtle(command, state):
if command == "F":
state = forward(state)
if command == "f":
state = translate(state)
if command == "+":
state = rotate(1, state)
if command == "-":
state = rotate(-1, state)
return statedistance は亀の1歩の長さ
drawcolor は描画色
angle は向きを変える角度
これらを引数に入れるかどうかという問題があるが,とりあえずはこのまま進めよう。
以上が最小限のタートルグラフィクスシステムだ。イニシエータとジェネレータを決め,distance なども設定し,置き換えシステムでコマンド列を作って turtle に渡せばよい。
描画面の設定は,たとえば次のようにしておこう。(はじめに書く)
import numpy as np
import matplotlib.pyplot as plt
plt.figure(figsize=(8, 8))
ax = plt.axes()
plt.axis([0, 8, 0, 8])
plt.xticks([])
plt.yticks([])コッホの雲形曲線を描いてみよう。
state = [[1, 1], 0] # 亀の初期状態 出発点とはじめの向き
angle = 60 / 180 * np.pi # 角 度数法 -> 弧度法
initiator = "F"
generator = {"F":"F+F--F+F"}
repeat = 4
distance = 6 * (1/3)**repeat
drawcolor = 'k'
# === 定義はここまで
com = initiator
for i in range(repeat):
com = com.translate(str.maketrans(generator))
for command in com:
state = turtle(command, state)
plt.show()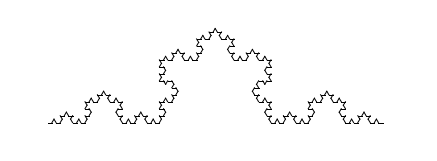
次は雪片曲線。はじめの位置とイニシエータ・ジェネレータ,1歩の長さを変える。
state = [[2, 2], 0] # 亀の初期状態 出発点とはじめの向き
angle = 60 / 180 * np.pi # 角 度数法 -> 弧度法
initiator = "F++F++F"
generator = {"F":"F-F++F-F"}
repeat = 4
distance = 4 * (1/3)**repeat
repeat = 0 のときはイニシエータの正三角形が表示される。
リンデンマイヤーの本「The Algorithmic Beauty of Plants」 には、次の例が載っている。いずれも,置き換えの対象は F だけで,ジェネレータの規則も1つだけ。
イニシエータ F-F-F-F
ジェネレータ F-F+F+FF-F-F+F
角度 90°
state = [[2, 6], 0] # 亀の初期状態 出発点とはじめの向き
angle = 90 / 180 * np.pi # 角 度数法 -> 弧度法
initiator = "F-F-F-F"
generator = {"F":"F-F+F+FF-F-F+F"}
repeat = 2
distance = 4 * (1/4)**repeat
drawcolor = 'b'イニシエータは正方形。ジェネレータが14文字なので,文字数が一気に増える。repeat = 3 でも3803文字となり,ちょっと時間がかかる。(下図右端)

イニシエータは同じで、ジェネレータと回数を変えた次の例も載っている。「The Algorithmic Beauty of Plants」Chapter 1 (p10)

「 f 描画しないで前へ進む」 も定義したので使ってみよう。
まずカントール集合。1辺を三等分し,中の部分を抜く。これを置き換えていく。こんどは置き換えが2文字,Fとfになるので,ジェネレータで2つ定義する。
state = [[1, 1], 0] # 亀の初期状態 出発点とはじめの向き
angle = 90 / 180 * np.pi # 角 度数法 -> 弧度法
initiator = "FfF"
generator = {"F":"FfF", "f":"fff"}
repeat = 2
distance = 2 * (1/3)**repeat次図は,上から repeat が 0,1,2 の場合である。

次は,「The Algorithmic Beauty of Plants」掲載の例。
state = [[3, 2], 0] # 亀の初期状態 出発点とはじめの向き
angle = 90 / 180 * np.pi # 角 度数法 -> 弧度法
initiator = "F+F+F+F"
generator = {"F":"F+f-FF+F+FF+Ff+FF-f+FF-F-FF-Ff-FFF","f":"ffffff"}
repeat = 2
distance = (1/4)**repeat
次はコマンドを増やして L-Systemsをひとまず完成する。
