
Cinderellaで数学:いろいろな曲線:円錐曲線に接するV型定木の頂点軌跡
「曲線の事典」(礒田正美他編著:共立出版 2009)に掲載のものです。
放物線,楕円に接しながら動く,角を固定したV型の定木の頂点の軌跡はどうなるのか,という問題です。
放物線
固定角が90°のとき,与えられた放物線の準線上を動き,そうでないときは双曲線上を動きます。
作図器の写真と解説図がありますが,作図器は,リンク機構ではなく,放物線に沿って動かすようになっているものです。Web上にある写真と,本の解説図です。

写真を見ると,放物線の形をした透明な板が置かれていることがわかります。これに接するように手で動かしていくわけです。
解説図の説明です。
焦点F、準線dで定義される放物線と放物線上の点Qに関する接線 $${t}$$ が与えられている。接点Qから準線へ垂線の足Hを下ろし、焦点FとHを結ぶ。焦点Fを通りFHに垂直な直線を引き、準線dとの交点をKとする。このとき,線分FKの垂直二等分線は放物線の接線となる。
このあと,K,P,Hが同一直線上にあることを説明しています。
放物線を先に描いて,直交する2本の接線を作図するのは大変ですが,この説明図にしたがって描くと,目的の接線が描けます。Cinderellaで作図してみましょう。
① 1直線と1点を取り,「焦点と準線で決まる放物線」ツールで放物線を描く。
焦点のラベルをFにしておく。
② 放物線上に点を取り,「点の曲線を加える」ツールで接線を描く。
点のラベルをQにしておく。
③ Qから準線に垂線をおろし,ラベルをHとしてFと結ぶ。
④ Fを通りFHに垂直な直線を引き,準線との交点をKとする。
⑤ FKの中点をとり,垂直二等分線をひくと,これが接線になる
点Qをドラッグすると,2本の接線との交点Pが常に準線上にあることがわかります。

V型定木の固定角が直角でない場合の説明もありますが,1本の接線を引いた後,「交角αで交わるように接線を引き」となっていて,これは作図ツールではできません。
90°の場合で,作図器風にしたものを次に載せました。
楕円
楕円の場合は,直交する場合だけ解説があります。

半軸の長さ a,b,焦点$${\rm{F_1}}$$,$${\rm{F_2}}$$ の楕円と,中心$${\rm{F_1}}$$,半径2aの円$${\gamma}$$がある。円$${\gamma}$$上の4点A,B,C,Dは,$${\rm{F_2}}$$で直線ABと直線CDが直交するように配置する。このとき、四角形ADBCの各辺の中点により作られた右図の四角形 QRTPは楕円に外接する。
< 中略 >
楕円に外接した長方形の頂点は常に中心O,半径$${\sqrt{a^2+b^2}}$$の円周上にある。すなわち,楕円に互いに直交する2つの接線の交点の軌跡は円になる。
この説明にしたがってCinderellaで作図しましょう。 作図しやすいように背景の方眼を表示しておきます。
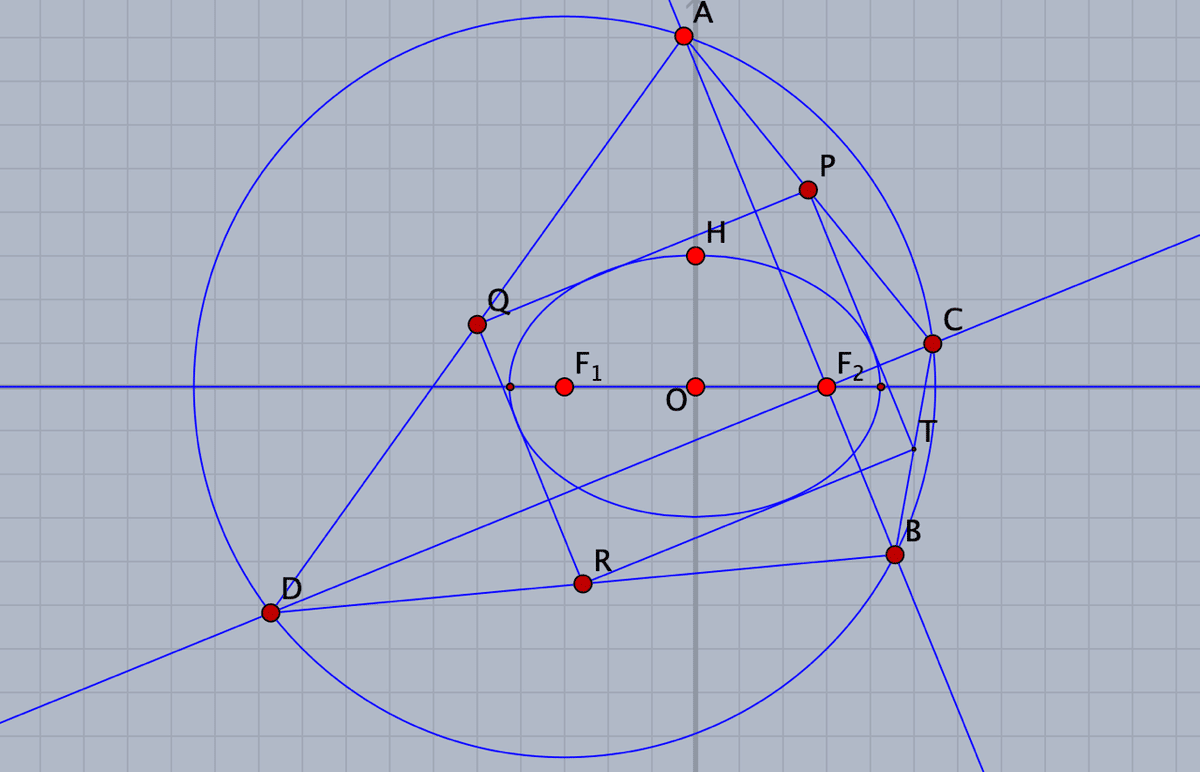
点Aをドラッグすると,長方形PQRTが楕円に接しながら動きます。
軌跡ツールを選んで,動かす点としてA,軌跡を描く点としてPを選ぶと,軌跡の円が表示されます。

見出し画像は,放物線の場合について作図器風にしたものですが,2次曲線上の点における極線をCindyJSがサポートしていないので,そのままHTMLに書き出してもWebでは動きません.Webで動かすには別の方法で作図する必要があります。興味がある人はやってみてください。
←Cinderellaで数学・情報 記事一覧に戻る
楕円
