
JavaScriptで画像の色を減色したかった話(k-means)
はじめに
画像を基に、イメージカラーを抽出することを目的に減色処理を実施します。
まずは、分かりやすいイラストを基にk-meansを実装してみました。
※下記の記事の続きです。
k-measn超概要
クラスタリングと呼ばれる、データを分類する手法の一種です。
今回は、Googleのfaviconを題材にして色を4つに分類するといったことをします。

上の画像を見ると背景の白or黒を除いて4色と感じますが、色と色の境目を拡大するとグラデーションになっており、ピクセル単位で考えると実際はもっと多くの色があることが分かります。(実際には59色ありました)

そのため、画像上の色は5色以上あるものの、これを4色に減色するといった処理を、色を4種類に分類することで実装します。
k-meansのアルゴリズム
手順
手順1:ランダムな重心を準備する(データを分類してから重心を作る手もある)
手順2:重心と各データとの距離を求め、各データは一番近い重心に分類する
手順3:上記の処理で全ての割り当てが変化しなかった場合、または、変化量が閾値を下回った場合に、収束したと判断して処理を終了する。それ以外の場合、新しい分類から重心を再計算して上記の処理2を実施する。
イメージ図
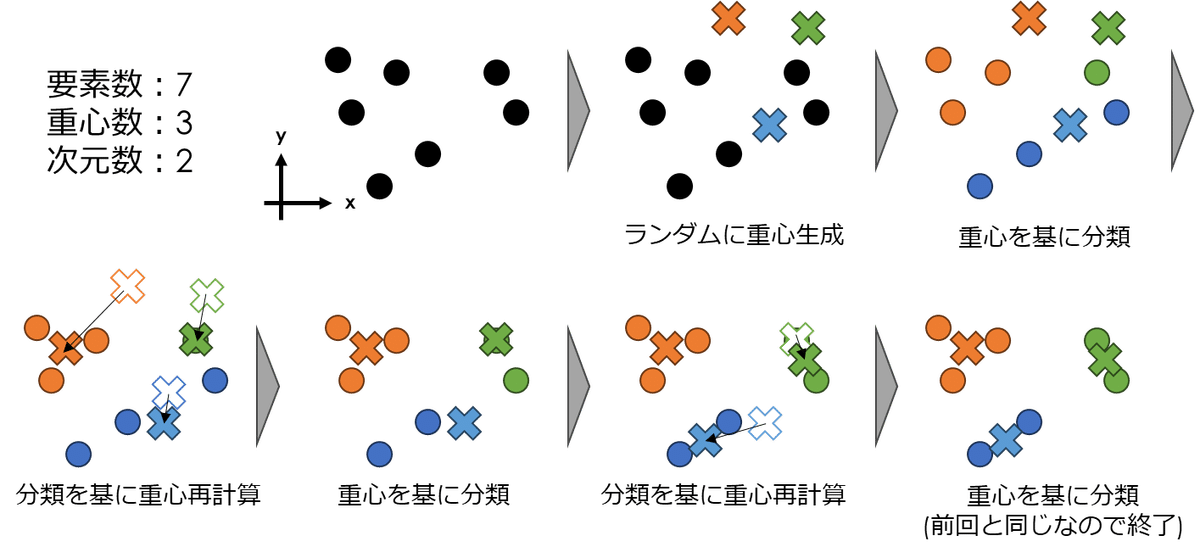
注意点
※分類前のデータのばらつきが小さい場合に手順1をランダムな重心にするとすべてのデータが一つの重心に分類されてしまうといったことがあったり、データが均一に広がっている場合に手順1を分類してから重心を作ると重心がすべて同じような座標にプロットされてしまい分類がうまくいかないことがあったりする。
※手順2はユークリッド距離で実装していますが、マンハッタン距離、チェビシェフ距離(左記3つを一般化したミンコフスキー距離)、マハラノビノス距離、ヘリンジャー距離、ハミング距離といったいくつかの距離があります。
※手順3は収束完了しないことを考慮して、試行回数の上限を設定したりします。
k-meansの欠点
調べると下記のような問題点が挙げられていました。
・初期値によるランダム性。試行ごとに結果が異なる。
→今回のコードでは5~6回に1回成功します。大抵は、分類されるデータがない重心が発生してしまいエラーが出てしましました。
・クラスタ数(重心数)を最初に決める必要がある
→今回は画像を見て5を固定にしていますが、汎用性がありません。
また、5固定の場合、5色未満の画像だとエラーになってしまいます。
・外れ値に影響を受ける
コード
imgDataはGoogleのfaviconのデータになります
imgDataは[r,g,b,a,r,g,b,a,...]といった形の1次元の配列なので、
arrDataを作り、[[r,g,b],[r,g,b],...]といった2次元配列に変換し、
変換後のarrDataをKmeansクラスに入れてクラスタリングを実行します。
※今回はnode.jsで実行しています。
※文字数が多すぎて投稿できなかったので、imgDataの中身は途中省略で書いています。
"use strict";
const imgData = [ 170, 113, 57, 9, 234, 83, 48, 37, 234, 83, 48, 37,... (略)... 56, 167, 93, 55, 54, 162, 93, 33, 170, 113, 57, 9];
const Kmeans = class {
// プロパティ
itr = 0; // 分類の試行回数
maxItr = 50; // 分類の最大回数
data = []; // データを格納した配列
dataLength = 0; // データの要素数
dimension = 0; // データの次元数。2つ目の[]の要素数
clusters = 4; // 何チームに分類するか
category = []; // データの各要素がどの重心に分類するか
categoryPrev = []; // データの各要素がどの重心に分類するか(前回分格納用)
gravityPos = []; // 重心を格納する座標の配列
// コンストラクタ
constructor(initData) {
// 値を初期化
this.data = initData;
this.dataLength = initData.length;
this.dimension = initData[0].length;
// 初期の重心を作成
this.initGravity();
}
// 配列の比較 (文字列に直して比較)
isEqualArray(arr1, arr2) {
return (JSON.stringify(arr1) === JSON.stringify(arr2));
}
// ランダムな整数値を返す
getRandomInt(min, max) {
return Math.floor(Math.random() * (max - min + 1) + min);
}
// 距離の定義を実施
calcDistance(a, b) {
let d = 0;
for (let i = 0; i < this.dimension; i++) {
d += (a[i] - b[i]) ** 2;
}
return Math.sqrt(d);
}
// 重心を初期化
initGravity() {
for (let i = 0; i < this.clusters; i++) {
if (!this.gravityPos[i])
this.gravityPos[i] = [];
for (let j = 0; j < this.dimension; j++) {
this.gravityPos[i][j] = this.getRandomInt(0, 255);
}
}
}
// データの要素ごとにどの重心に分類するか調べる
categorizeData() {
// category[]を初期化
this.categoryPrev = this.category;
this.category = [];
// 各重心との距離をdistanceToGravityPosに格納し、最小値のインデックスをcategory[]に格納。
let distanceToGravityPos = [];
for (let i = 0; i < this.dataLength; i++) { // 各要素ごとに処理を実施
// 各重心までの距離を計算
distanceToGravityPos = [];
for (let j = 0; j < this.clusters; j++) {
distanceToGravityPos.push(this.calcDistance(this.data[i], this.gravityPos[j]));
}
// 重心までの距離の配列の中の最小値のインデックスを取得する
const min = distanceToGravityPos.reduce((a, b) => a < b ? a : b);
const minIndex = distanceToGravityPos.indexOf(min);
this.category.push(minIndex);
}
}
// 分類された要素を基に重心を更新する。
calcGravityPos() {
// カテゴリごとの要素数をカウントする配列と要素の合計を格納する配列を準備する
// counter = [0,0,0]
// sums = [[0,0,0],[0,0,0],...]
let counter = [];
let sums = [];
for (let i = 0; i < this.clusters; i++) {
counter[i] = 0;
sums[i] = [];
for (let j = 0; j < this.dimension; j++) {
sums[i][j] = 0;
}
}
// カテゴリごとの要素数と要素の合計を計算する
// counter = [10,5,20]
// sums = [[1020,1500,25500],[5,105,12750],...]
for (let i = 0; i < this.dataLength; i++) { // 各要素ごとに処理を実施
let cat = this.category[i];
counter[cat]++;
for (let j = 0; j < this.dimension; j++) {
sums[cat][j] += this.data[i][j];
}
}
// 新しい重心を計算
for (let i = 0; i < this.clusters; i++) {
if (!this.gravityPos[i])
this.gravityPos[i] = [];
for (let j = 0; j < this.dimension; j++) {
this.gravityPos[i][j] = Math.floor(sums[i][j] / counter[i]);
}
}
}
// クラスタリングのメインロジック
main() {
this.itr++;
this.categorizeData();
this.calcGravityPos();
// categoryの配列が前回と変わってなかったら処理終了
if (this.isEqualArray(this.categoryPrev, this.category)) {
return;
}
// 試行回数が最大回数を超えていたら処理終了
if (this.itr > this.maxItr) {
return;
}
this.main();
}
};
let r = 0;
let g = 0;
let b = 0;
let a = 0;
let arrData = [];
// imgData=[r,g,b,a,r,g,b,a,...]を
// arrData=[[r,g,b],[r,g,b],...]に変換
for (let i = 0; i < imgData.length; i += 4) {
r = imgData[i]; // r
g = imgData[i + 1]; // g
b = imgData[i + 2]; // b
a = imgData[i + 3]; // a (透過度)
if(a==0)continue;
arrData.push([r, g, b]);
}
// KmeansクラスにarrDataを入れてクラスタリングをする
const km = new Kmeans(arrData);
km.main();
// 結果を#xxxxxx形式で表示
let rgb2hex = function (r, g, b) {
return "#" + ("000000" + (r * 256 * 256 + g * 256 + b).toString(16)).slice(-6);
};
for (let i = 0; i < km.gravityPos.length; i++) {
console.log(rgb2hex(km.gravityPos[i][0], km.gravityPos[i][1], km.gravityPos[i][2]));
}
※背景透過領域はr=0, g=0, b=0, a=0となっており、不透明度0(=透明度100%)の黒となっているので、これは除外しています。
実行結果
C:\work\>node kmeans.js
#e94334
#fbbb04
#000000
#4086f3
#33a754色を見てみるといい感じになりました。
使用率の方が実際に使われている色で、クラスタリングは重心のため、わずかに色コードが違ってしまっています。

おわりに
k-meansを実装してみました。
クラスタ数(重心数)の判定や、直感に近い値が出るような初期値の選定、処理失敗時の処理、背景透過領域の無視の処理をするなど、細かいカスタマイズの実施を今後していきます。
また、今回のイラストならk-means使うより色の利用率ベースで抽出した方がよさそうなので、画像特性の判別も必要そうです。
