わり算に2つの意味があるワケ
わり算って「なんか他の計算と違うな~」って思った事はありませんか?
「小学生の頃、わり算が苦手だったな~」って人もいるかもしれません。
その感覚、正しいです!
わり算は本当に他の計算と少し違うんです。
何が違うのか…それは、わり算には2種類のパターンがあるのです。
例をあげて見てみましょう。
パターン①(等分除)
10個のりんごを2個ずつに分けると何人の子に配れますか?
式)10 ÷ 2 = 5 答え)5人
パターン②(包含除)
10個のりんごを2人に同じ個数だけ分けると何個になりますか?
式)10 ÷ 2 = 5 答え)5個
どうでしょうか?
パターン①と②、ちょっと違いますね。
ちなみに等分除、包含除という名前は参考であげただけなので、覚えなくて大丈夫です。
同じ10個のりんごを分けているし、式も同じ。
それなのに答えは5人と5個。
そしてパターン①は1人2個なのに、②は1人5個。
そう、わり算の計算に2種類の考え方があるのです。
つまり
パターン①
同じ数ずつ分けたら、何個のグループができるのか?
パターン②
いくつかのグループに同じ数ずつ分けるには何個にしないといけないのか?
となっていて、違いますよね。
きっとわり算が苦手だと思っていた人、なんかちょっと違うと思っていた人
こういう所に引っかかったのではないでしょうか。
でも小学生には、このモヤモヤ、戸惑いの説明をするのは難しいですよね。
大人だってここまで考えないから、中々分かってもらえない。
でも、ここで一つ踏み込んで考えていれば、良いアドバイスがあれば違ったのかも。
今回はそんな人たちのために解説したいと思います。
わり算の意味とは
そもそもわり算って何を求めているのでしょうか?
わり算の意味を考えていきましょう。
例えば、上の例だと
10 ÷ 2 = 5
ですね。
これは、「10の中に2のかたまりがいくつあるのか」ということ。
ちなみに、2のかたまりになれなかった残りが"あまり"です。
(わり算の定義による解釈は色々ありますが、この解釈だと汎用性が高いです)

つまりパターン①は、わり算の意味そのままの計算式ですね。

10個のりんごの中の2個のりんごのかたまりが5つあるのが分かります。
え、じゃ、パターン②はどういうこと?って思いますよね?
では、なぜパターン②も同じ式で求められるのか、考えていきましょう。
まず、りんごを分ける2人の名前をAさん、Bさんにしましょう。
2人に分けるので、りんごにAさんのシールA、BさんのシールBを
はっていくことにします。
2人とも同じ個数になるように端から順にAとBを交互にはっていきましょう。
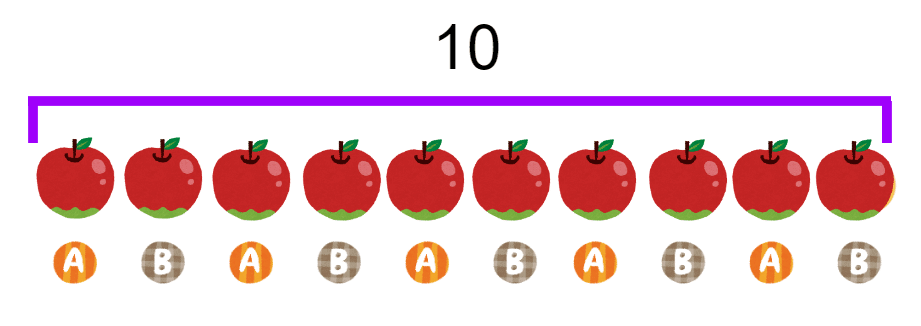
勘の良い人はもう気付かれたかもしれませんね。
このA、Bのシールを1セットにして考えてみましょう。
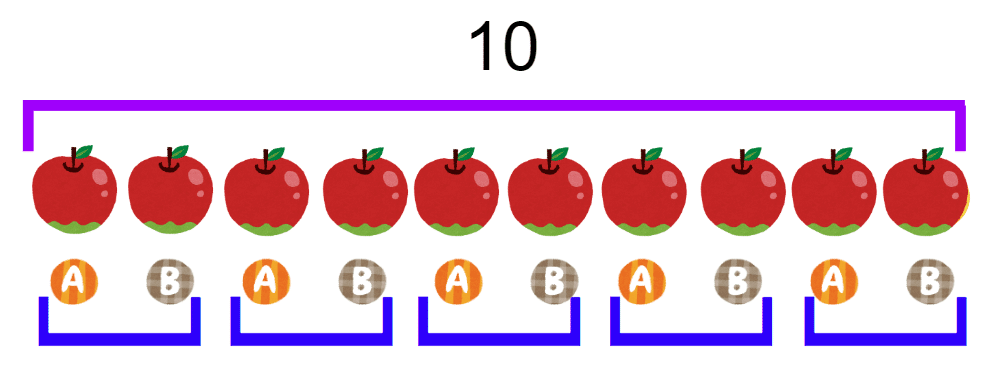
この図に見覚えがありますね。
そう、これはパターン①と同じ図ですね!
つまり、AとBのセットが5セットできるという事です。
もちろん1セットの中にはAとBは一つずつしかないので、
Aさんは5個のりんご、Bさんも5個のりんご、という事になります。
まとめると
パターン①はわり算の意味のまま、
パターン②はわり算の意味からグループ分けをして
答えを求めている、つまり応用なのです。
わり算には確かに2種類あります。
でも、それはなんて事はなく1つは単なる応用なのです。
ただこれを算数の時間に先生が説明すると
小学生だと混乱する子も出てきてしまうかもしれませんね。
気付く子と気付かない子、両方いると思います。
気付いた子こそ「考え」「感じて」、そしてモヤモヤしてしまうのです。
もしお子さんがモヤモヤして何が分からないか分からないけど分からない、
と言い出した時には、チャンスだと考えてください。
そのモヤモヤを晴らす事ができれば、算数が好きになるきっかけになるかもしれません。
