
【脳波解析】相互情報量
「Analyzing Neural Time Series Data Theory and Practice」(Mike X. Cohen and Jordan Grafman)をまとめるシリーズももうすぐ終わりです。今回は、Chapter29をベースに、相互情報量について、説明をしていきます。
前回のnoteはこちら↓
また、今回のnoteをまとめる上で、弊ラボの先輩の坂本嵩さんの以下のスライドを超絶参考にしています!そちらのチェックも是非!!
エントロピー
相互情報量を理解をするため、まずエントロピーの説明をします。エントロピーとは、事象の不確実性のことで、高エントロピーは不確実性を、低エントロピーは確実性を示し、エントロピーは以下の式を用いて計算することがでいます。
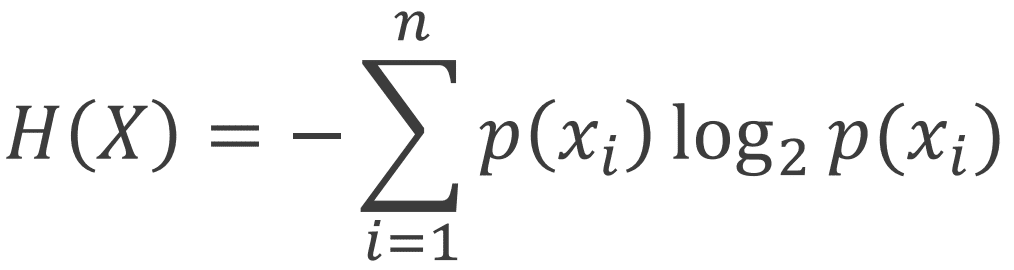
ここで、logは確率の期待値を示し、計算するときは log(0) = −∞ に注意(端っこが0だと-∞になってしまう可能性有)し、微小値を足して回避しましょう。また、上記の式からもわかるように、エントロピーは時間に依存しません。時間窓内の値をヒストグラムに集めるだけなので、時間配置は影響がなく、時間関係をぐちゃぐちゃにしてもokです。

(上図は坂本嵩さんのスライドから拝借しました。)
上図において、青のビン(棒)で書かれた図は高エントロピーを、赤のビンで書かれた図は低エントロピーを示しています。
また、エントロピーは不確実性の指標としても使え、脳をシステムと捉えシステムの制約の多さを表します。具体的には、時間&トライアル方向にデータを集めて計算して求めることができます。
さらに、同時に起こる確率(同時確率)の不確実性の変動性を表すものとして、結合エントロピーがあります。これは以下の式で求めます。

相互情報量
相互情報量とは、2変数の重複した情報のことで、正 / 負 / 線形 / 非線形 問わない関係性を求めます。パワー・位相データ両方に適用することができ、特にパワー値に関してはビンで区分けを行い、ヒストグラム上で非連続なデータにすることができます。さらに相互情報量はCross-Frequency Coupling(次のnoteで説明します)にも応用することができます。相互情報量は
𝑀𝐼(𝑋 , 𝑌 ) = 𝐻(𝑋) + 𝐻(𝑌) − 𝐻(𝑋 , 𝑌 )
(ここでH(X)はXのエントロピー、H(X,Y)はXとYの結合エントロピー)で表すことができます。データ数の影響に気を付ける必要があります。データ数が減ると、ヒストグラム上にて集まる(べき)ところにデータが集まらなくなり、HやMIが上がってしまいます。その対策として、1)ビン数を変える、2)ノイズが一様なら無視、3)以下の式を用いる、が挙げられます。

また、相互情報量においてノイズは大きく影響します。ノイズも一緒にプロットする(分布だから平均で消えない)ためサンプリングレートをしても意味がなく、フィルタなどの下処理を通して出来るだけ綺麗なデータを使いましょう。
さらに、Lagged Mutual Information、すなわち方向性を持つ相互情報量では、どれだけ時間窓がずれた時にMIが最大になるかをみることができます。そのため、ずらすのは一周期分だけで十分です。
時間方向/トライアル方向の相互情報量
コネクティビティをみたい時に必ずぶちあたるのが時間方向(over Time)かトライアル方向か(over Trial)か問題です。(相互情報量に限った話ではありませんが、)時間方向の相互情報量について、時間分解能が高くなり位相同期の活動を捉えやすくなります。一方、トライアル方向は時間分解能は下がりますが、非位相同期の活動も捉えやすくなります。ただし、データがトライアル数に限定されるため、筆者は時間及びトライアル方向の両方に着目することを推奨しています。両方に着目することでデータが増加し、ロバスト性を向上することができます。
相互情報量を適用する際に気を付けること
エントロピー/相互情報量はビン数に依存します。ビンが増えることでノイズの影響が大きく乗ってしまうため、エントロピーが上がります。そのため、エントロピーはビンは多すぎても少なすぎてもダメで、条件/被験者/電極間でビン数を揃え、また、ビン数の影響をまともに受けてしまうため時間軸によって変えないようにしましょう。それではビン数はどうやって決めればいいのでしょうか。一例として、"Freedman -Diaconis rule"を紹介します。Freedman -Diaconis ruleは以下の式で計算します。

ここで、Q_xは第1四分位数と第3四分位数の距離、nが総データポイント数、max(x)-min(x)がデータxの最大と最小の差を表します。要するに、第1-3四分位数を天井関数にかけてrangeとの比を出しましょうってノリですね。Freedman -Diaconis ruleを用いると、ある程度いい感じなヒストグラムがかけます。また、他にもScott’s rule やSturger’s ruleなどでビン数を決めることができます。
相互情報量の統計
相互情報量でのデータとして、データは正規分布していないため、パラメトリック検定では不十分です。そこでPermutation Testを用いて検定にかけます。ノンパラメトリック検定におけるPermutation Testについて、以前のnoteで説明しているので、是非そちらを参考にしてください。Permutation Testでは、帰無仮説の中でランダムにデータを作り、その中でのヒストグラムのずれ(i.e., 観測値をZ化してp値を計算)をみます。ここで、帰無仮説として2変数間に関係がない(相互情報量がない)とすると、時間をズラしても値は変わらない、ということを検証します。
最後に、このノートにスキを押してくれると、とても嬉しい&更新のモチベが爆上がりします!ここまで読んでくださり、ありがとうございました。
<謝辞>
このnoteを書く上で、弊ラボの坂本嵩さんにご協力いただきました。ありがとうございます。
