
【脳波解析】ノンパラメトリック Permutation test
本ページでは「Analyzing Neural Time Series Data Theory and Practice」(Mike X. Cohen and Jordan Grafman)のChapter33をベースに、ノンパラメトリックPermutation testについて、説明をしていきます。ノンパラメトリック検定については前回のnoteで紹介していますので、そちらをご覧ください。
前回のnoteはこちら↓
そもそもPermutation testとは?
ノンパラメトリック permutation testは、脳波解析において重要な概念です。 Permutation testとは、 2変数間に関係がないという帰無仮説を立てた上で、ランダムに時間をずらして分布を作成、比較をする検定のことです。これ、時間周波数結果の統計的評価にめっちゃ使えます。というのも、データ/パラメータの散らばりの想定をしておらず、更に、多重比較のための適切な補正を分析時に取り込めるためです。
パラメトリック検定は正規分布を仮定し、検定統計量は帰無仮説下で期待される分布と比較されます。一方、ノンパラメトリックPermutation testの分布は、実際に取得したデータから構成されて、帰無仮説が真である場合の検定統計量の観察をします。ので、データまたはパラメータが正規分布してる時は、どっちでも同じような結果になります。していないときは、ノンパラメトリック検定を使いましょう。また、ノンパラメトリック検定はブートストラップ法とは異なります。どちらもデータのスワップという点では類似していますが、Permutation testは、帰無仮説が真のときに観測値が得られるときの確率を決定しますが、ブートストラップ法は、データの復元抽出のことで、データ特性(i.e., 平均、分散)やパラメーター推定値の信頼区間を定義します。
帰無仮説分布を作成しよう
ノンパラメトリックPermutation testを実行する際には、はじめに帰無仮説分布を作成する必要があります。帰無仮説分布は、以下の手順を繰り返すことで作ることができます。
1) (例えば、)2変数において、一方の変数で活動が活発すると仮定
2) 2変数のデータを一部スワップ
3) 帰無仮説として、2変数間に違いがないことをとしてたてる
4) t検定を用いて、観測値と帰無仮説による分布と比較し、棄却できるか検証
この手順を、たくさん繰り返すことで、十分な結果を得ることが可能となります。この際、ラベルとトライアルの双方がスワップされるため、シャッフルを行う次元やコンディションは仮定に準じます。
では、繰り返しは何回行えば良いのでしょうか。ごちゃ混ぜにするとエラーが大きくなってしまいます。更に、Nトライアル/2コンディション存在するときの多項係数は、
N!((N_A)!(N_B)!)
となります。N: 全トライアル数、A/B:コンディション内のトライアル数です。例えば、Aが3トライアル、Bが2トライアルあるとすると、多項係数は
5!3!2!=1440
・・・。たった5トライアルでこれです。脳波でやったら大変なことはなんとなくわかりますよね。何が言いたいかって、全部やったら多すぎるし、時間がかかりすぎるということです。 ただし、繰り返しの回数が増えるほど、帰無仮説分布はより正確になります。そこで、数学的根拠はないそうですが、脳波データの場合は千回くらいやると十分になります。また、ノイジーなデータがあるときは繰り返しを増やしましょう。
P値の計算
帰無仮説検定統計量の分布が作れたところで、つぎに、P値を求めます。p値の求め方には大きく2通りあげられます。
1) 実際に数を数える方法
はじめに、帰無仮説検定統計量の数を数え、その後、観測データの数を数えます。それぞれのデータ数の差を帰無仮説検定統計量の数で割ったものがp値となります。そのため、帰無仮説検定統計量の数がめちゃめちゃ多いと、p値は0に近づきます。
2) 観測値と帰無仮説分布の統計的propertiesを比較
はじめに、観測値をZ値に変換する標準化を行います。Z値は以下の数式
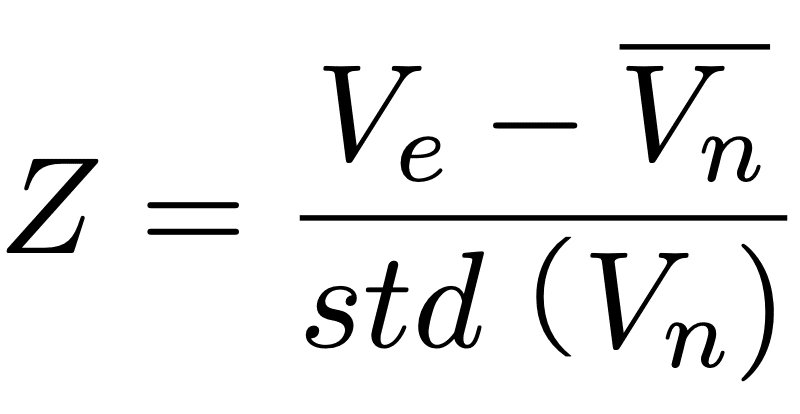
で求めることができ、このとき、V_nはoserved effect test statisticを、overline{V_n}は、帰無仮説検定統計量の平均を示します。要するに、"Z値=平均とのばらつき/ばらつきの平均(標準偏差)”ってことです。その後、ガウスの確率密度分布を用いて、z値をp値に変換します。
脳波データでは、それぞれのピクセルでにおいてp値/z値を計算することで、時間ポイント/周波数帯/電極にまたがる検定を行います。これにより、各時間-周波数-電極ポイントで帰無仮説分布への組み込みが可能となります。また、データはランダムにシャッフルされるため、帰無仮説の分布を計算するたびにp値が変化することに注意する必要があります。
多重比較の補正
多重比較の補正では、評価されるテストの数でp値を分ける必要があります。例えば、ボンフェローニ法は有意水準を調整する方法で、どうしても複数回検定をしなきゃいけない時に使います。ボンフェローニ法では、有意水準は通常の有意水準α(0.05)をN検定数で割ったものとなります。そのため、検定数が多いほど有意になりにくく、真の値も有意でないと識別される可能性あり、不適切な場合もあります。さらに、ボンフェローニ法はテストの独立性を仮定していますが、脳波では、隣接時間/周波数/電極が非独立です。さらに、有意水準について、時間周波数ポイントの数など、テストの数は任意に決められられるので、テストの数に基づいた補正ではなく、情報量にも基づいた補正が好ましいです。
ボンフェローニ法に対し、Permutation testは多重比較の複数の補正を組み込むのに適しています。というもの、Permiutation testでは、テストの数に基づいた補正ではなく、結果に存在する情報に基づいた補正を行うためです。また、相関した多次元データの影響を発見するのに十分な感度を残す、p値の閾値を提供します。
多重補正問題の問題解決には、ピクセルレベルではなく、マップレベルでの検証をする必要があります。が、帰無仮説マップ内の各ピクセルに帰無仮説分布が存在しています。帰無仮説分布は、多重比較の相関と共に時間周波数からの統計値を含んでおり、各要素は単一時間周波数ポイント/電極と関連していません。また、permutationsが実行された時間周波数-電極スペースの情報を反映しています。このように、Permiutation testは多重比較の補正でとっても使えますが、Permutation testだけでなく、FDR(false discovery rate correction)、厳しめな未補正の統計的閾値、 正規確率場理論(Gaussian random field theory)などの多重補正のやり方もあります。
FDRとは、仮説検定を複数回行なった場合に、誤って棄却される帰無仮説の割合のことです。値の分布内で第一種の過誤の確率を制御する際に使います。 第一種の過誤とは、帰無仮説が真であるのにもかかわらず、帰無仮説を偽として棄却してしまう誤りのことで、FDRの分布は、テスト数にも基づいていることに注意しましょう。
ピクセルベースのPermutation testを用いた補正
Permutation testを用いた補正では、ピクセルベース及びクラスターベースの 2 種類があげられます。まずは、ピクセルベースの補正について説明します。ピクセルベースでは、最も極端な統計値を持つpermutation testの、各反復からのピクセルを含む分布を作成します。そのため、クラスターベースの統計に比べ、統計的な厳しさがあります。また、各ピクセルでは帰無仮説分布を保存せず、Permutation testの各反復で、全ピクセルにわたる最も極端な帰無仮説統計値のまとめを保存します。
計算方法として、はじめに、今までに紹介した方法を用いて、permutation testを実行します。これは、帰無仮説のもとで検定統計量を生成するためです。各反復において、最も極端な帰無仮説検定統計値を持つ、片側検定の場合は 1 つ、両側検定の場合は 2 つのピクセルの値をマトリックスに収納します。この流れを全反復で繰り返すことで、正の最大ピクセル値と負の最大ピクセル値の 1 つ(片側検定)、または 2 つ(両側検定)の分布が作成されます。その後、p = 0.05 などで閾値設定を行います。ここで、分布そのものはマップレベルであり、結果の情報量に基づくことに注意してください。これより、データが少なくても、検定的には問題がなく、単一ピクセルで統計の有意性が図れる、という利点があります。
クラスターベースのPermutation testを用いた補正
つぎに、クラスターベースの補正を紹介します。そもそも、クラスターとは、時間/周波数/電極空間の隣接しているポイントのグループを指します。クラスターベースの分布についても、補正は結果の情報量に基づいています。クラスターベースの補正の考え方は、データの自己相関により、隣接ピクセルがしきい値以上の値を “十分に”もってたらすごい!って感じです。“十分に”、とは、結果の解像度(how many 抽出周波数、データがダウンサンプリングされたか)によります。
クラスター補正の方法は 2 通りあります。1つ目がは、事前に定義した時間/周波数ポイント数よりも少ないクラスターを消去するやり方です。しかし、主観的でデータドリブンでない可能性が高くなります。そのため、以下のような方法が推奨されます。
1) permutation testを行い、帰無仮説検定のための各反復で、p<0.05など、未補正レベルで時間周波数マップに閾値(precluster threshold)を適用
2) 帰無仮説の反復マップの閾値処理を行う
このやり方は、データが正規分布しているかどうかにより異なります。データが正規分布している場合については、パラメトリックt検定、または、相関係数の結果であるp値を使用します。データが正規分布していない場合、または、していないと想定される場合は、まず、各ピクセルで帰無仮説分布を作成します。その後、 ノンパラメトリック兼ピクセルベースの有意性閾値を使って閾値を設定することで、閾値処理を行います。
3) 未補正のp値を使って、観測された統計量マップを閾値処理
4) 帰無仮説で想定される最大クラスター分布の95%に入らないクラスターを除去
クラスターベースの多重比較補正の特徴として、閾値(precluster threshold)が補正時の閾値に影響されることが挙げられます。そのため、閾値(precluster threshold)は理に叶った大きさにする必要があります。また、補正時の閾値については、precluster thresholdと同じかそれより厳しめな大きさ、具体的には、permutation test でクラスターを生成する時と同じ大きさにする必要があります。また、大きいクラスターに超sensitive(上記手順4参照)であり、それが統計的有意かはわからない、という欠点もあります。
統計処理するには何使えばいいの?
脳波データの統計処理はどうやってやればいいのでしょうか。MATLABのStatistics and Machine Learning Toolboxは、1 /2 因子のANOVA 関数のノンパラメトリックな手法を提供しています。しかし、パラメトリック統計は、EEG分析パッケージで実装されてないことが多く、あってもルーチンが非常に少ないです。そのため、データをSPSS/SAS/Rなどの統計ソフトウェアパッケージにエクスポートする必要があります。ただし、ベイズ統計に関しては、SPM8にはベイジアン手法に基づく統計ルーチンがあり、役立つMATLABのサードパーティツールボックスもたくさんあるので、どのような処理を行いたいか、その統計処理にMATLABが十分に対応しているかによるでしょう。
最後に、このノートにスキを押してくれると、とても嬉しい&更新のモチベが爆上がりします!ここまで読んでくださり、ありがとうございました。
