
【統計の勉強】多群比較の手順③〜検定法を決めるまでの流れ
【追記】2020年5月25日 ノンパラメトリック検定の部分を少し変更しました。
こんにちは。生命科学系研究者のえいこです。
実験データときちんと向き合おうと決意して、統計とRの勉強過程をnoteにまとめています。
これから多群比較をするためのコードを書いていくにあたって、きちんと多群比較の知識をつけないとと思って多群比較の勉強をしています。
多群比較の手順①ではGoogleスプレッドシートを使ったサンプルデータの作り方
多群比較の手順②では多群比較検定の必要性
について、まとめてきました。
今回は、検定法を決めるまでの流れをざっと把握してみようと思います。
検定法を決めるまでにやること
なんだか聞いたことがあるから、とりあえずone-way ANOVAしておく?というのはやってしまいがちですが、ちゃんと検定法の意味を理解して使っていないことになってしまいます。
別に統計学の専門家にはならなくて良いとは思いますが、最低限「なんでこの検定法を採用したのか?」という質問には答えられるようにしておきたいと思います。
で、私がネットサーフィンをして検定法を決めるのにこんな順番で決めれば良いのではないか?と思ったのをまとめます。
1. 正規性を確認する
(2. 対応があるか無いか)
(3. 分散は同じかどうか?→パラメトリック検定の場合)
4. 比較対照群はあるのか?
と言ったところでしょうか?まず、データが正規分布であるかどうかを確認して、パラメトリック検定をするか?ノンパラメトリック検定をするかを決めるのが良いのでは無いかと思っています。
【追記】2020年5月25日
正規性を決める方法としてShapiro-wilk検定を採用していますが、この検定の帰無仮説は「正規分布である」なので、pの値が有意水準を下回らなかったからと言って、積極的に正規分布であることを支持しているという結果ではありません。
パラメトリック検定をしてみて、結果を考察するのが良いと思いますが。ここでは、正規性をもとにパラメトリックにするかノンパラメトリックにするか決定するコードを書いていきます。
パラメトリックの結果かから、他の検定に移行する分岐も考えていますが、最初の前提のところの部分なので、ざっくり分けています。
正規性の確認をする
Irisのデータを使って正規性を確認する方法をまとめています。
今回も、Shapiro-Wilk test (シャピロ・ウィルクの検定)を使って準備したサンプルデータの正規性を検定してみたいと思います。
#Shapiro-wilk test
tapply(data$value, data$group, shapiro.test)
という実行結果になりました。(RStudio Cloudだとコンソール画面の文字のコピペができなくなりました...)
p値を見る限りは、コントロールもAもBも帰無仮説は棄却されず「正規分布であろう」という結果になっています。
念のためヒストグラムも見ておきましょう。
####ヒストグラムを描くよ####
library(ggplot2)
hist<- ggplot(
data,
aes(y=..density.., fill=group, color=group)
)+
scale_y_continuous(expand=c(0,0))+
theme_classic()
hist<- hist+
geom_histogram(
aes(x=value),
position = "identity",
alpha = 0.7,
bins = 40,
)+
geom_density(aes(x=value), alpha = 0.5)
hist
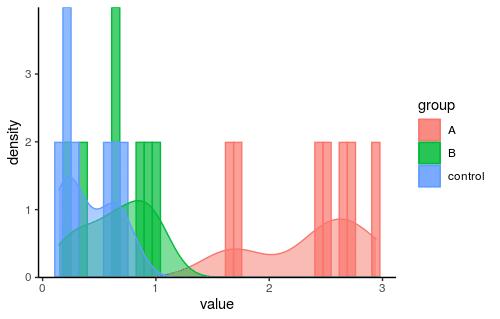
これを「正規分布」と断言して良いものか?という感じでもありますが...
積極的に正規分布では無いとも言い切れないようです。
シャピロ・ウィルク検定の結果を踏まえると、今回用意したデータは正規分布に従うみたいだったので、パラメトリック検定を採用する。
という感じになります。
多群比較のパラメトリック検定とノンパラメトリック検定
パラメトリック検定とノンパラメトリック検定の基本的な違いについてはこちらの記事にまとめています。
パラメトリック検定とノンパラメトリック検定、どちらを採用するか?はまずデータの正規性を見るということでした。

こんな感じの分類です。
統計の勉強をあまりしていなかった時には、何も考えずにパラメトリック検定を採用して、一元配置分散分(one-way ANOVA)析をして、違いがあればそれぞれの群について統計処理する。としていました。
が、実は事前に一元配置分散分析(one-way ANOVA)が必要な検定とそうで無い検定があるようです。しかもよく使われるTukey-Kramerとかは実は一元配置分散分析(one-way ANOVA)は必要ないのです。

というのも、分散値(F値)を使わないで統計量を計算する手法だから。(詳しい計算方法は調べていません、興味が湧けばのせておきます)
ここで頭に入に入れておくことは、よく使われるTukey-KramerやDunnett検定を使う時には事前にone-way ANOVAをする必要はあまり無いということでした。(Wikipediaなどを調べると「ANOVAと併用して用いられる」と書いてあったりするのですが...)
また、Tukey-Kramer法は各群が同じような分散であることを前提とした検定なので、もし厳密に検定をするとしたら、Levene検定をして等分散であるかを確認してからTukey-Kramerに進むのが良さそうです。
等分散でなければ、Bonferroni補正を使って検定していくことになります。
ちなみに...
Tukey-Kramer検定は群を総当たりで比較する
Dunnett検定はコントロール群と比較する
と覚えておけば使いやすいですね。
さて、次にノンパラメトリック検定の場合を見てみます。
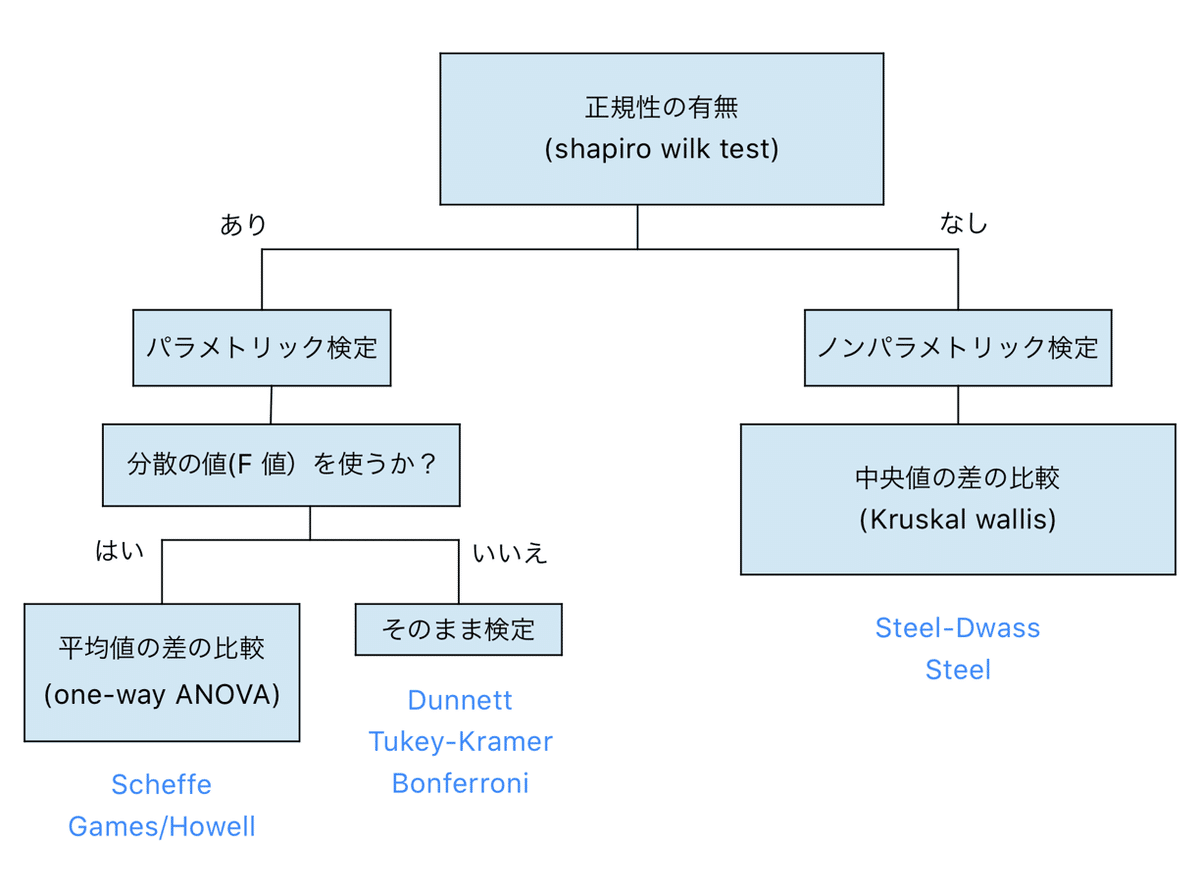
one-way ANOVAのノンパラメトリック版がKruskal-Wallisの検定です。Kruskal -Wallis検定は中央値の差の比較をする検定。
その検定をした後に、Tukey-Krammerのノンパラメトリック版であるSteel-DwassやDunnettのノンパラメトリック版であるSteel検定を行なっていくようです。
Steel-DwassやSteel検定はWilcoxon順位和検定(Mann-Whitney U検定)の考え方をもとにした検定方法です。
データの値そのものを使うのではなく、データの大きさ順に順位をつけて、比較していくので分散の大きさや正規性はあまり気にしなくても良いみたい。
ノンパラメトリック検定で覚えておけば良いことは、Kraskal-Wallis検定をしてSteel-Dwassなどの検定をしていくという流れだということです。
【追記】2020年5月25日
Kraskal-Wallis検定の結果で帰無仮説が棄却された場合、平均値が異なる群があるということでSteel-Dwass検定やSteel検定に移ります。
Kraskal-Wallis検定はRでデフォルトで入っている関数を使うので、漸近検定であることを頭に入れて検定しておきます。
もし、サンプルサイズが小さくて正確検定の値が気になるようだったら、kSamplesパッケージを使えば計算できるみたいなのでやってみようと思います。
Steel検定でpの値が出てくるパッケージを探していますが、なかなか見つかりません。
Steel検定ではなくて、Dunn/Bonferroni検定を使うことを検討しています。
(ソースはこちら。)
今回勉強した多群検定の流れをまとめておきます。
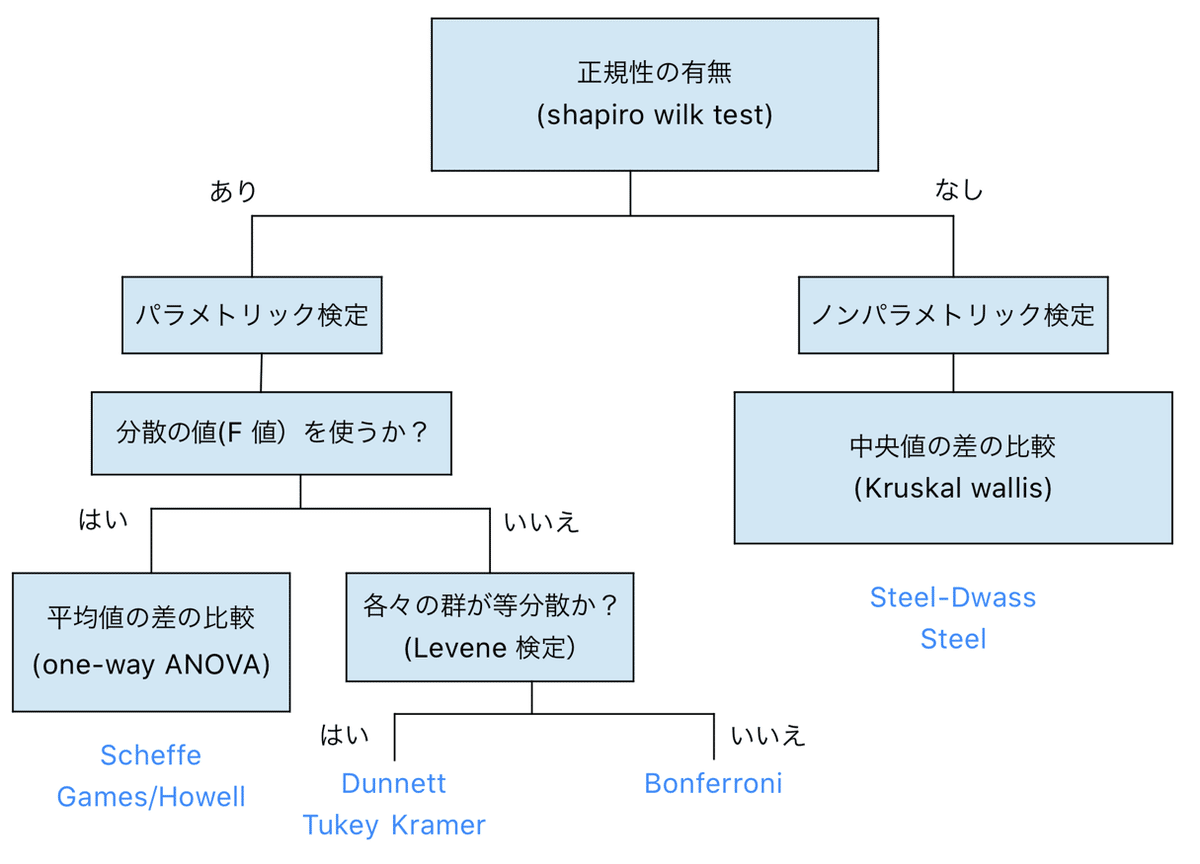
この樹形図はRのコードを書く時にすごく重要なので覚えておきます。
樹形図の分岐はif文で分岐できるので!
研究の世界でよく使われる、検定を使うコードにしていきたいと思っているので、使う検定はDunnet, Tukey-Kramer, Bonferroni, Steel-Dwass, Steelあたりだと思います。
次回は、少しずつコードを書きながら勉強していこうと思います。
それでは、また!
〜この記事を書くにあたってこちらの記事を参考にしました〜
いいなと思ったら応援しよう!

