
【ImageJ】ImageJマクロでLUTを変換する
生命科学系研究者のえいこです。今回は、ImageJマクロを使って「LUTを変換する」をしていきたいと思います。
マクロを使うと自由にグレースケールの調整ができるようになります。さらに、同じような条件で撮影して同じ解析をしたい写真が何枚もある場合にはいちいち条件を調整しないで済むので、大量のデータを一括で出力して比較できるので楽ちん。
画像とLUTについてはこちらの記事で紹介しているので、「LUTって何?」と言う人はこちらの記事もみてみて下さい。
【ImageJ】画像のコントラストを変えるとは?
ImageJマクロを始めようと思っているんだけど...どうやって始めたら良いかわからない!と言う人はこちらの記事に初歩の初歩から書いているので是非参考にしてみてください。
【ImageJ】ImageJマクロを使ってみる
今回の記事で参考にしているのは、「ImageJで始める生物画像解析」です。
それでは早速、ImageJマクロのコードを書いていってみましょう。
ImageJマクロを使う前に〜線形グレースケールと非線形グレースケール とは?
白黒の画像のグレースケールを線形から非線形に変換してみましょう。「グレースケールを線形から非線形に変換する」と言うのは一体どう言うことなのでしょう?
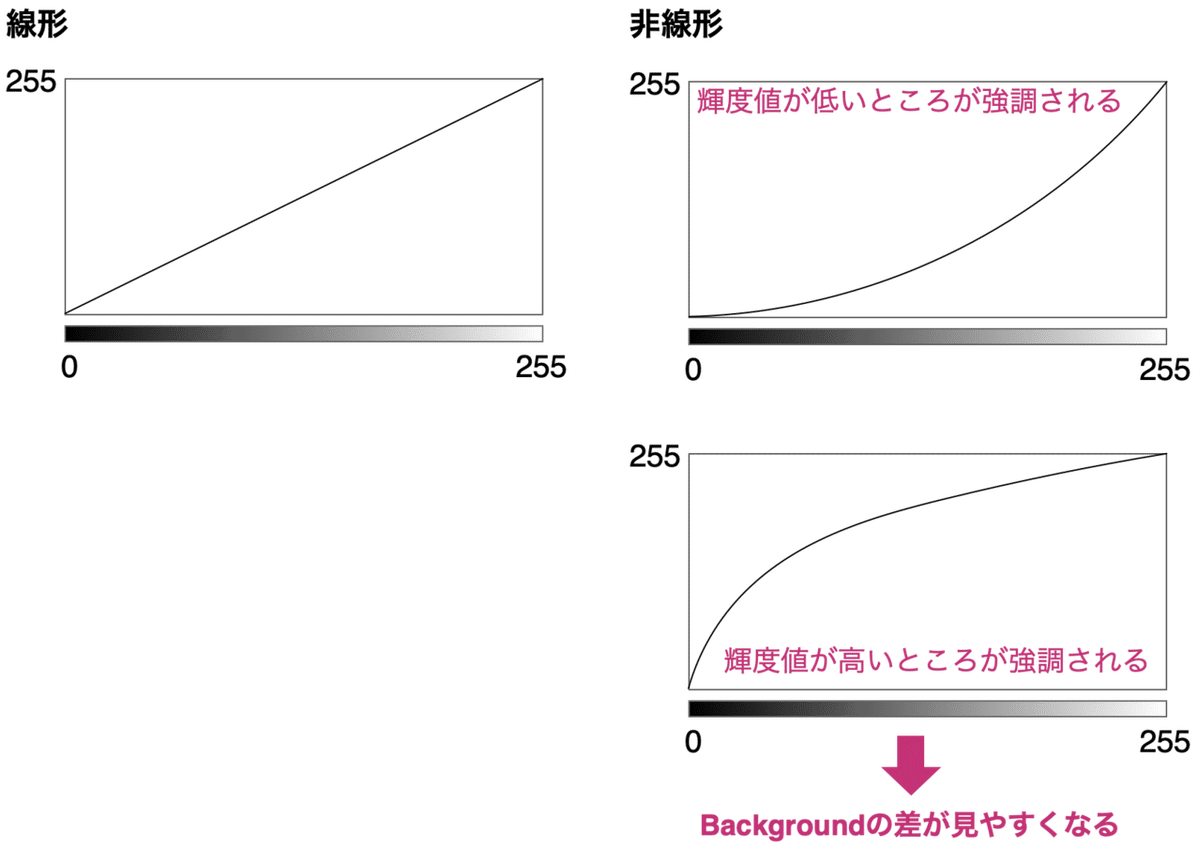
元々線形のグレースケールを非線形にすることで、輝度値が高いところが強調されたり、低いところが強調されるようになります。下に凸の非線形グラフにすれば白の背景の色の違いがわかりやすくなり、上に凸の非線形グラフにすれば黒の背景の色の違いがわかりやすくなるのです。
つまり、非線形グラフにすることでバックグラウンドの色の濃淡の違いをはっきりみることができるようになると言うわけです。
サンプル画像を使って、白黒画像のLUTを非線形に変換してみましょう。
ImageJマクロを使ってグレースケールを線形から非線形に変換する
グレースケールを線形から非線形に変換するコードがこちら。
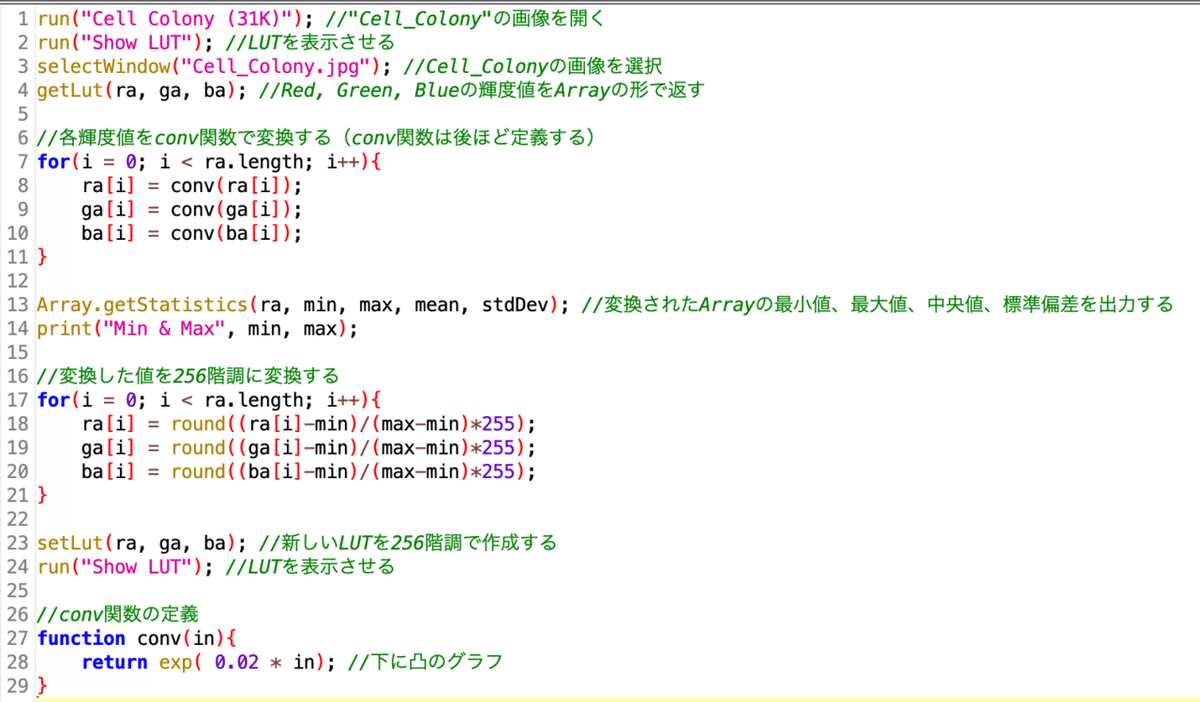
上のコードをスクリプト画面に打ち込んで、"Run"を押すと...
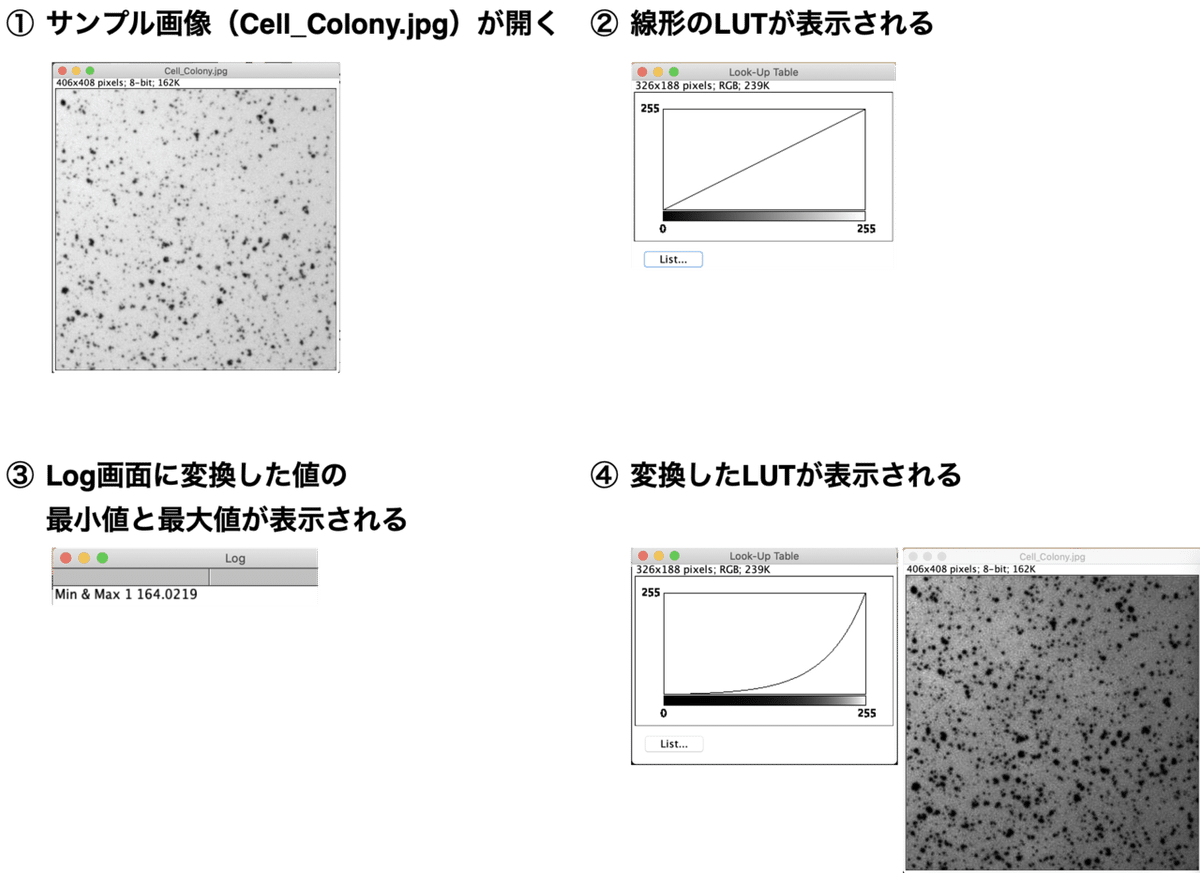
順番にマクロが実行されて、LUTが変換されました。下に凸のグラフにすると、画像全体が黒くなり、背景が左上が明るくて右下にいくと暗くなってくるのがわかりますね。
では、同じ画像を使って上に凸のグラフを書いてみましょう。やることは、"conv"関数の定義の式を変えるだけです。
function conv(in){
return 164 - exp(-1 * 0.02 * in); // 上に凸のグラフ
}に書き換えて"Run"を押してみます。最終的に表示されたLUTはこちら。
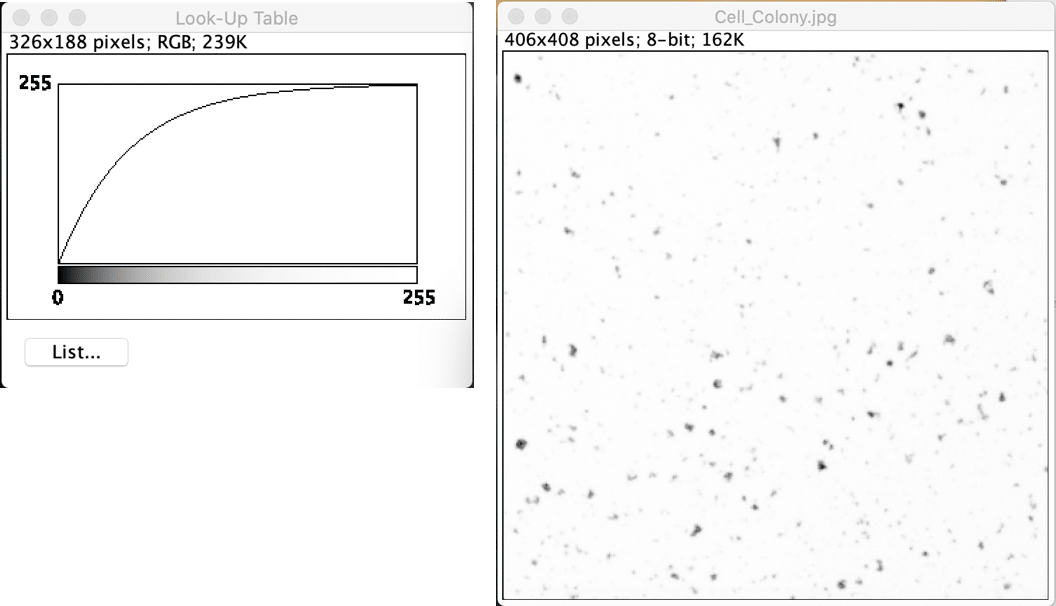
下に凸のグラフに比べて全体が白っぽくなっていて、色の濃淡があまりはっきりしない画像になりました。
【おまけ】ガンマ値補正するスクリプトを書く
線形のグレースケールから非線形のグレースケールにImageJマクロを使って変換できるようになりました。最後におまけで、「ガンマ値」を補正するスクリプトを書いて終わりにしようと思います。
画像解析をしていると時々出てくる「ガンマ値」。ガンマ値を変えると画像がはっきりくっきりになったりするなーと言う印象は持っていましたが、具体的にどんなものかはよく知らなかったので調べてみました。
ガンマ値とは、画像の階調の応答性を示す数値。また、入力機器のガンマ値に応じた最適カーブに画像の階調を補正することをガンマ補正と言う。
Wikipediaより
「??」Wikiの冒頭の説明では、ちょっとよくわかりません...もう少し読み進めてみると...
ディスプレイなどの画像を出力する機器では、入力値(デジタルデータの数値)と出力値(表示される画像の明るさ)の関係は一次関数的な関係ではなく、"Vout = Vin ^γ"と言うカーブに近似した関係であることが多いそうです。(入力値と出力値が直線関係である場合は"γ=1"と言います)
各ディスプレイで固有のガンマ値を持っているので、ディスプレイの出力に応じてガンマを補正すれば、意図した通りの画像が表示されるようになるのです。
γ<1の場合の場合は上に凸のカーブとなり明るい階調の画像に、γ>1の場合は下に凸のカーブとなり暗い階調の画像として出力されます。
例えば、ガンマ値が2.2のパソコンディスプレイで適切に表示されている画像をガンマ値が1.8のパソコンで表示させた場合、実際のガンマ値はγ=1.8/2.2<1となり想定したものより明るい画像になってしまいます。画像の入力から出力までのガンマの値が1になるように補正することが「ガンマ補正」です。
ちなみにMacのパソコンの場合は、ガンマ値が2.2。多くのテレビでもガンマ値2.2が採用されているようです。
今回は、この"Vout = Vin ^2.2"を1に補正する変換をしてみましょう。(元々非線形で出力されるのものを線形に出力されるようにに変換すると言うこと)
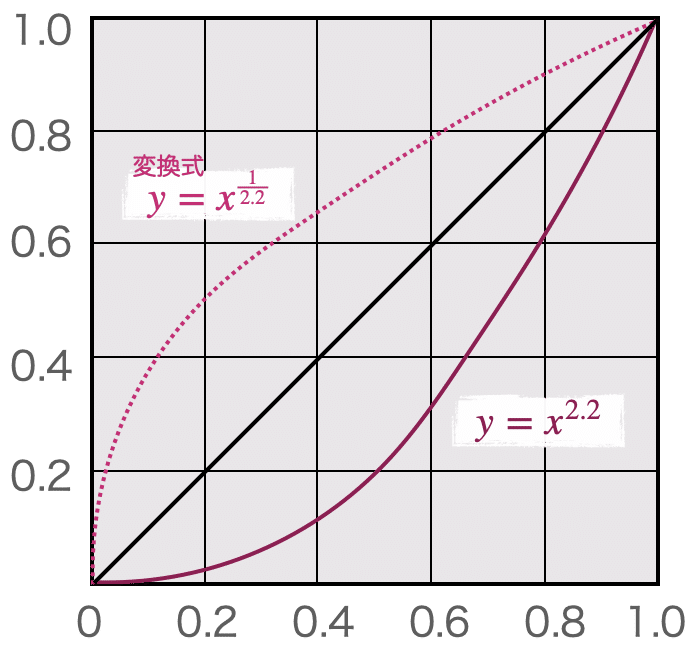
y=x^2.2のカーブをy=xの一次関数に変換する式は、y=x^(1/2.2)となります。この式を"conv"関数の定義を変更すればガンマ補正ができると言うことなので、早速、数式を作ってマクロを回してみましょう。
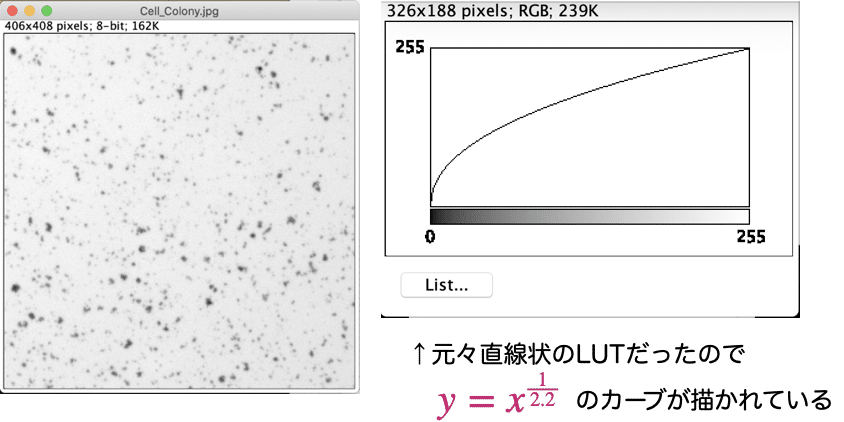
これが「ガンマ補正」と言うらしいです。コロニーの写真ではわかりにくいですが、写真や映像の方がガンマ補正の効果がわかりやすいんじゃないかなと思っています。
次回は画像データの種類についてまとめていきます。
それでは、また!
参考資料
いいなと思ったら応援しよう!

