【統計の勉強】箱ひげ図ってどうやって読み取るの？

最近の科学系の論文では、ただの棒グラフにエラーバーをつけたグラフは「NG」という風潮になりつつあります。その代わりに「箱ひげ図」が使われるケースが多くなっていますね。棒グラフが表すのは「平均」と「データのばらつき（標準偏差・標準誤差）」だったのに対して、箱ひげ図って何を表しているの？その見方を知らない人は多いのではないでしょうか？

今回は統計検定2級を勉強する中で学んだ「箱ひげ図」の見方について簡単にまとめようと思います。（※統計検定では2回に1回は出るかなり頻出の範囲です！）

**********

「分位点」について知っておこう！

いきなり「箱ひげ図について」ではなく、基礎知識として知っておきたい「四分位点（quatile）」についてまとめておきましょう。

四分位点とは？

データの小さいものから順番に並び替えて、データの数を四等分した時の3つの分割点のこと。
第1四分位点(Q1)...25%分位点
第2四分位点(Q2)...50%分位点（中央値）
第3四分位点(Q3)...75%分位点

言葉だけだとよくわからないので、図でまとめてみましょう。

・データの数が奇数の場合

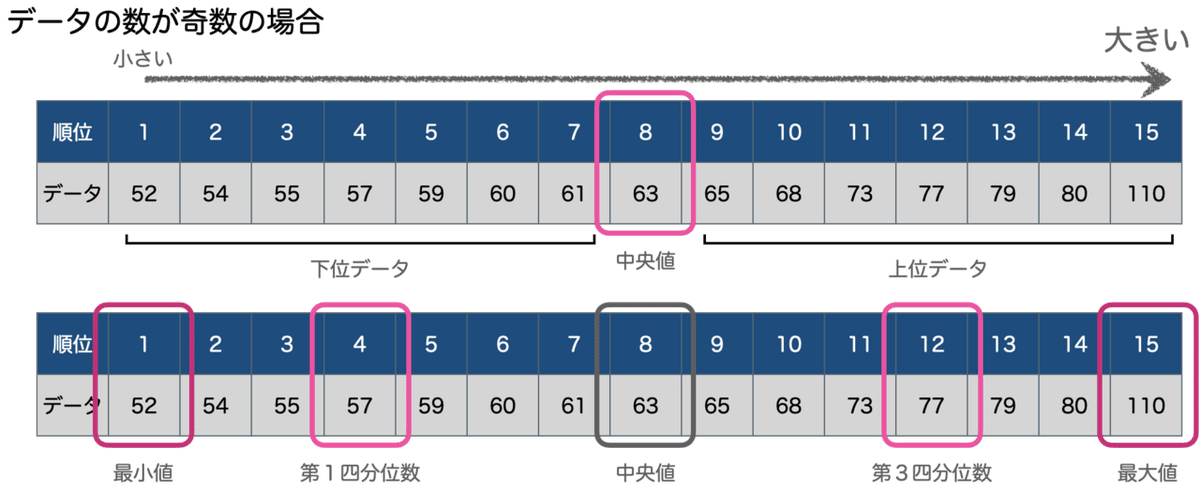
データの数が奇数の場合は、中央値や他の四分位値（数）が各データに当てはまるのでわかりやすいですね。

では、データの数が偶数の場合はどうでしょう？

・データの数が偶数の場合

偶数の場合（今回の場合）は中央値はデータ数が奇数の時のように各データに当てはめるのではなく、中央を挟む2つのデータの平均を中央値とします。第1四分位数も第3四分位数も同様に考えます。

箱ひげ図を描いてみる

箱ひげ図は最小値、最大値、第1四分位数、第3四分位数、中央値がわかれば描けるようになります。

先ほどのデータの並びを体重の計測結果だと仮定して、奇数の場合と偶数の場合に分けてグラフを見てみましょう。

・データの数が奇数の場合

下の図はRの"ggplot"パッケージのgeom_boxplot()関数を用いてグラフを書いたものです。（コードはこの記事の最後の方に載せておきます）

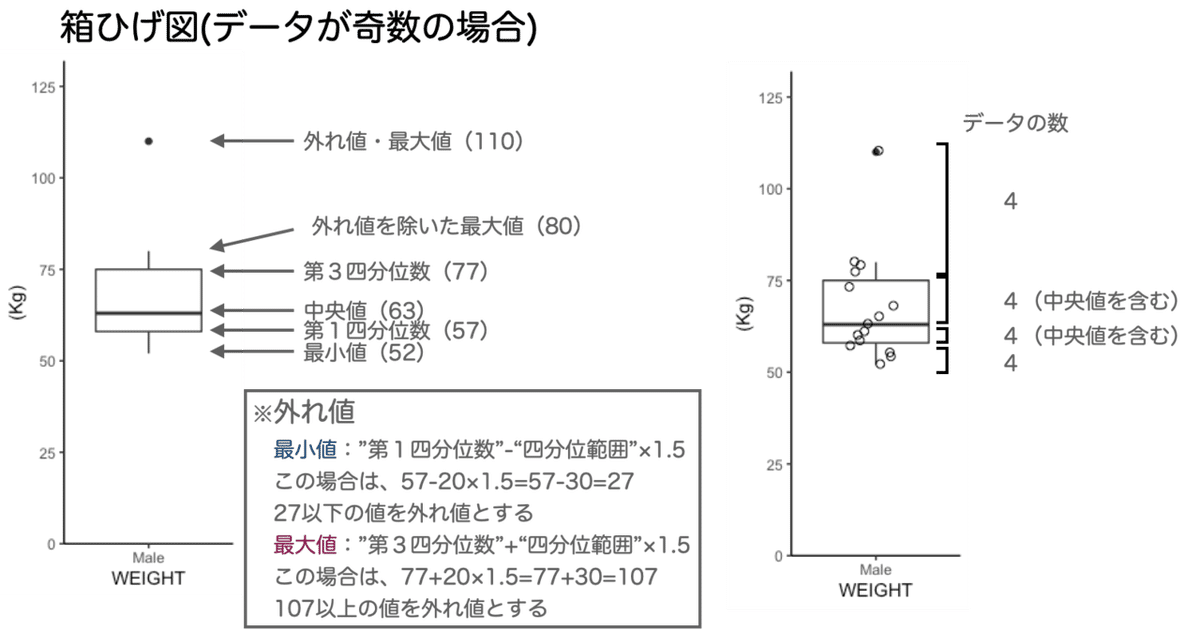
左側の図はデータを入れ込んでそのまま箱ひげ図を作ったものです。最小値は箱ひげの下側のひげの下端、最大値は箱ひげの上側のひげの上端、第1四分位数は箱の下端、第3四分位数は箱の上端、中央値は箱の真ん中の線としてそれぞれ描かれているのがわかります。（）何で示したのはそれぞれのデータの値です。

今回のデータは最大値が「外れ値」だったので黒いドットで最大値が表示されていますが、外れ値が無い場合は箱ひげの上側のひげの端が最大値となります。

「外れ値」について
外れ値の定義は曖昧でこれといって定義されていないようです。統計検定では外れ値の扱いを以下のように定義してから出題されていました。
最小値："第1四分位数"-"四分位範囲"×1.5以下の値（今回のデータの場合は27以下）
最大値："第3四分位数"+"四分位範囲"×1.5以下の値（今回のデータの場合は107以上）

さて、右側のグラフは左側の箱ひげ図にデータのプロットを重ね合わせたものです。最小値〜第1四分位数までの間にあるデータが4、第1四分位数〜中央値までの間にあるデータが4、中央値〜第3四分位数までの間にあるデータが4、第3四分位数から最大値（今回は外れ値も数える）の間にあるデータが4。と各データの数が均等になっていることがわかります。

・データの数が偶数の場合

データの数が奇数の場合と同様に偶数の場合の箱ひげ図も見てみましょう。

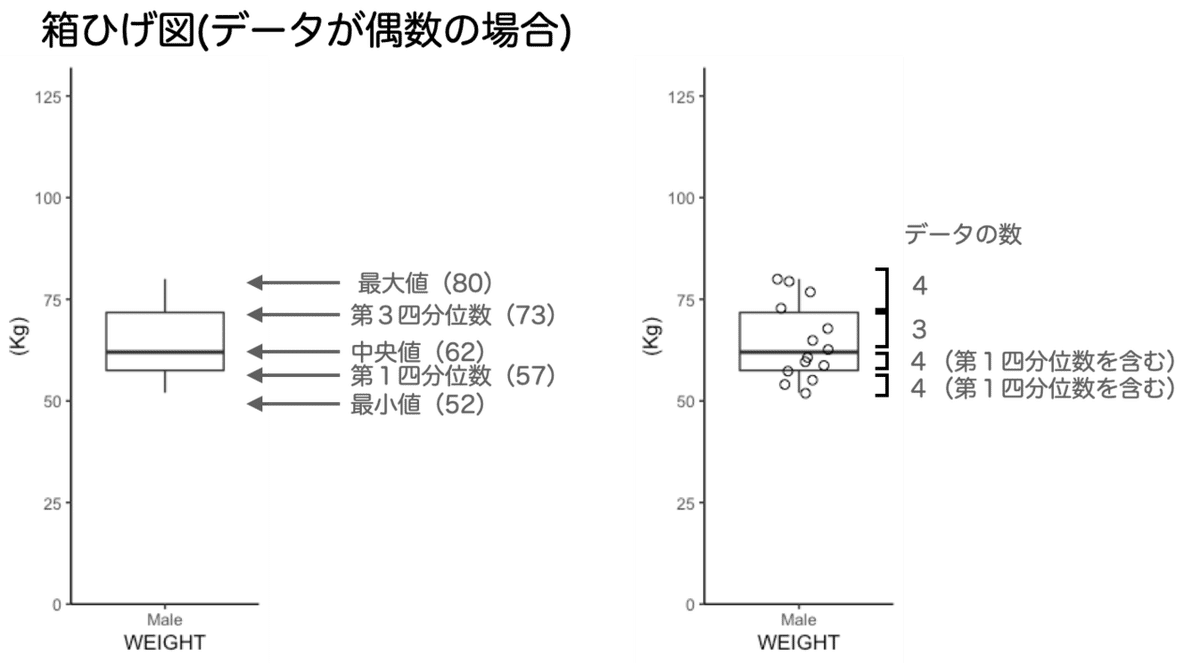
今回は外れ値が無いのですっきりしていますが、奇数の場合と同様に各線がデータの最小値、最大値、各四分位値を表しています。

右側の図のようにドットプロットを重ね合わせると、奇数の場合のようにきれいに同じデータの数では無いものの（中央値がデータの値そのものでは無いので）均等にデータが配置されていることがわかります。

**********

箱ひげ図が読めれば統計検定の問題も解ける！

箱ひげ図の読み方は、ほぼ毎年出題されています。箱ひげ図の読み取りができれば、得点源の一つになるので覚えておいて損はないでしょう。

また、論文などで描かれるグラフも箱ひげ図が主流になりつつあるので、読めるようになっておかないとデータの解釈ができないってことも起こってくるのです。箱ひげグラフが出てきたら、データのばらつきを表していることを意識して読み取れるようにしていきたいものですね。

それでは、また！

【おまけ】箱ひげグラフを書くRのコード

今回の記事の中で図に使った箱ひげグラフを書いたRコードをまとめておきます。

・箱ひげグラフ（奇数データのグラフ）

#install.packages("tidyverse")
library("ggplot2")
weight <- c(52, 55, 65, 80, 73, 63, 68, 59, 60, 57, 61, 77, 79, 54, 110)
sex <- rep("Male", 15)
x <- data.frame(SEX = sex, WEIGHT = weight)

g <- ggplot(x, aes(x= SEX, y = WEIGHT))+geom_boxplot()+
 scale_y_continuous(expand = c(0,0), limits = c(0, max(x$WEIGHT)*1.2))+
 labs(x = "WEIGHT", y = "(Kg)")+
 theme_classic()
plot(g)
ggsave(filename = "boxplot.png", plot = g, dpi = 100, width = 2, height = 4.5)

・箱ひげグラフにデータプロットを重ね合わせたもの（奇数データのグラフ）

#install.packages("tidyverse")
library("ggplot2")
weight <- c(52, 55, 65, 80, 73, 63, 68, 59, 60, 57, 61, 77, 79, 54, 110)
sex <- rep("Male", 15)
x <- data.frame(SEX = sex, WEIGHT = weight)

g1 <- ggplot(x, aes(x= SEX, y = WEIGHT, shape = SEX))+geom_boxplot()+
 geom_jitter(size = 2, width = 0.2)+
 scale_shape_manual(values = c(1))+
 scale_y_continuous(expand = c(0,0), limits = c(0, max(x$WEIGHT)*1.2))+
 labs(x = "WEIGHT", y = "(Kg)")+
 theme_classic()+
 theme(legend.position = "none")
plot(g1)
ggsave(filename = "box-dotplot.png", plot = g1, dpi = 100, width = 2, height = 4.5)