
【特集】線形単回帰モデル 第2部 ツールの活用
特集
この特集記事は、統計検定2級の出題内容に沿って、最小二乗法で推定する線形単回帰モデルの概略をまとめるものです。
この記事は2部構成の後編です。
【2つの記事】
第1部:概要
数式、計算を通じて統計検定2級レベルの線形単回帰分析を学びます。
第2部:ツールの活用(★この記事)
EXCEL、R、Pythonを用いて線形単回帰分析を実践します。
第1部のリンクはこちら。
この記事は、Windows PC で3つのツールを用いて、統計検定2級出題レベルの単回帰分析を行います。
・EXCEL
・R
・Python
お手元のデータを用いてサクッともりもり回帰分析を行うことで、データの理解、回帰分析の理解が促進され、統計検定2級の出題内容の深い理解に繋がるものと信じています。
まずはツールの使い方に慣れて、回帰分析に手軽に取り組めるようになることを目指します。
記事の力点をツールの操作・手順に置きます。
回帰分析の出力結果の読み解きは、ぜひ【第1部】をお読みください。
さらにツールの活用を希望する場合は、ぜひ入門書・専門書を手にとって、進めてください。
この記事がみなさまの学習のきっかけになれたらなら嬉しいです!

参考書籍
この記事は統計検定2級公式テキスト、および、統計検定2級公式問題集CBT対応版に準拠して書きました。
📕公式テキスト:1.6.4 回帰直線(32ページ~)、5.1.1 線形単回帰モデル(163ページ~)など
📘公式問題集
利用データ
統計検定2級公式問題集CBT対応版の問題10-1-1の「コーヒーデータ」を利用します。
問題集では1991~2015年を対象にしていますが、この記事では期間を延長して1991~2019年までを対象にします。
次のリンクはデータ入手元の「国際コーヒー機関」の統計データページです。
【出典記載】
「Total production - Crop Year : 1990- Present」
「Retail Prices - Annual Averages : 1990- Present」
(両データともに、国際コーヒー機関 International Coffee Organization)
(http://www.ico.org/new_historical.asp)
【コンテンツ編集・加工の記載】
記事の記載にあたっては、出典記載の資料を加工して作成しています。

【コーヒーデータの概要】
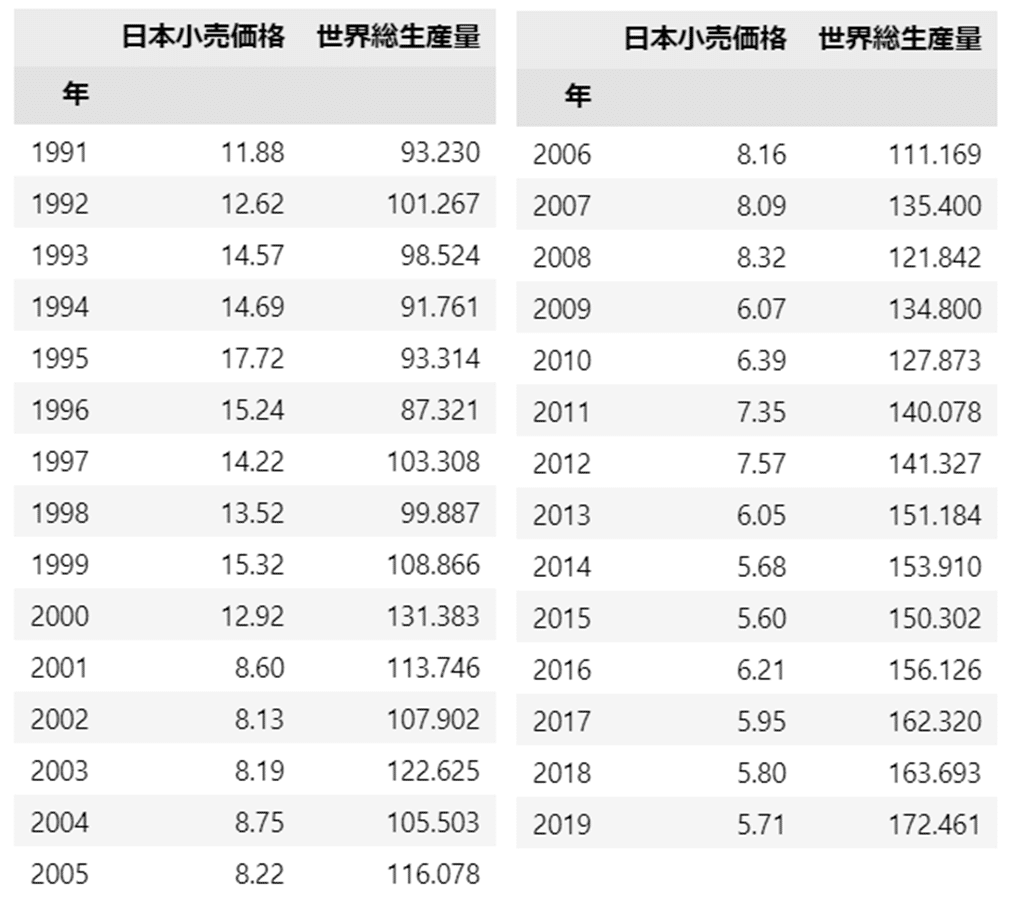
コーヒーデータは次の2つの量的変数で構成されています。
■ 項目「日本小売価格」
1991年から2019年までの29年間の日本の年平均小売価格(単位:米ドル/ポンド)
■ 項目「世界総生産量」
1990/91年から2018/19年(Crop year)までの29年間の世界年間総生産量(単位:100万袋)
CSVファイルのダウンロード
こちらのリンクからコーヒーデータのCSVファイルをダウンロードできます。
R、Pythonのコードを動かす際に必要なデータです。
1. EXCEL による単回帰分析
(1) 3つの回帰分析機能
EXCELには主に3つの回帰分析機能があります。
◆ グラフ機能
◆ 分析ツール
◆ LINEST 関数
用途に応じて使い分けできそうです。
・ビジュアル:グラフ機能
・詳細分析:分析ツール
・回帰係数だけ知りたい:LINEST関数
いずれの機能もサクッと動かせるので、使い勝手良く回帰分析を実行できます。
この記事では3つの機能を動かします。
3つの完成イメージを収納したEXCELサンプルファイルを共有いたします。
お手元で完成イメージを確認しながら、EXCELの回帰分析機能をお楽しみください。
EXCELサンプルファイルのダウンロード
こちらのリンクからEXCELサンプルファイルをダウンロードできます。
「【特集】線形単回帰モデル_データ」シートに「コーヒーデータ」をセットしています。


(2) グラフ機能
① 完成イメージ
「近似曲線のオプション」を利用して、散布図に回帰直線、回帰式、決定係数$${R^2}$$を表示します。
回帰式の回帰係数は最小二乗法で算出されます。
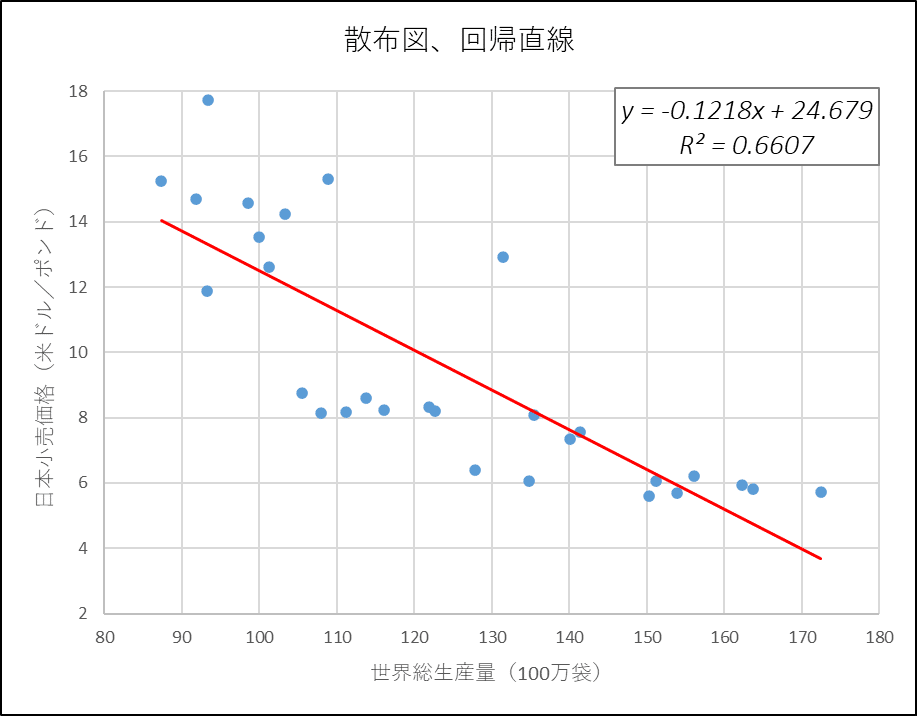
各観測データ点に対する回帰直線の当てはまり具合をビジュアルで「感覚的に」確認できます。
また、回帰式と決定係数$${R^2}$$を表示することで、傾きの強さ(説明変数1単位の変化による目的変数の変化の度合い)や、モデルの当てはまり具合を「客観的な数値」で確認できます。
このグラフを見ていて、気になり始めたことがあります。
近年、世界的にコーヒーの消費量が大幅に増加していると言われています。
世界の総生産量が増えても、消費量が大幅に増えれば小売価格の低下は起きにくくなるような気がします。
このグラフに無い2020年以降の状況も知りたいです。
可視化によってさらに深掘りしたくなることこそ、データ分析の愉悦なのです!
② 操作手順
■ メニュー:散布図を挿入
メニューより、「挿入」① > グラフの散布図② > 「散布図」③ を選択します。
EXCELシートに四角のグラフオブジェクトが挿入されます。
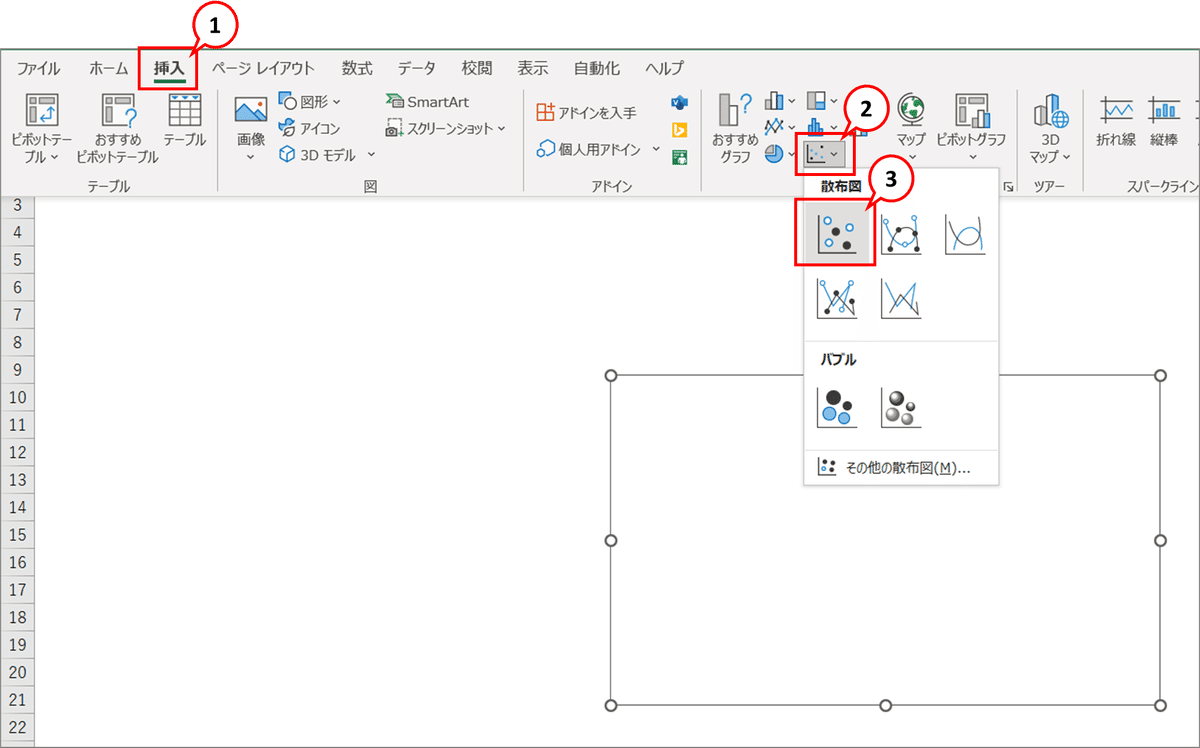
■ データの選択
グラフオブジェクトを右クリックします④。
メニューの「データの選択」⑤を指定します。

■ データの追加
「データソースの選択」画面の「追加」ボタン⑥をクリックします。

■ 系列の編集
「系列の編集」画面で、系列名、系列Xの値(グラフの横軸)、系列Yの値(グラフの縦軸)⑦を指定してOKボタンをクリックします。
再度「データソースの選択」画面が開きます。OKボタンをクリックします。

■ 近似曲線の追加
グラフオブジェクトをクリックして右側に現れる「+」メニュー⑧をクリックします。
メニューの「近似曲線」にカーソルを近づけると出現する「>」⑨をクリックします。
「その他のオプション」⑩をクリックします。

■ 近似曲線の書式設定
「線形近似」⑪を指定します。
「グラフに数式を表示する」と「グラフにR-2乗値を表示する」⑫をチェックします。
散布図に青い点線の回帰直線、回帰式、決定係数$${R^2}$$が表示されます。

線や文字を適宜修正して、グラフを仕上げます。

(3) 分析ツール
① 完成イメージ
「分析ツール」の「回帰分析」を利用して、回帰分析の各種統計値、グラフ、残差等の明細データを作成できます。
統計検定2級で出題される「統計ソフトウェア」と同じレベルの出力結果を得られます。


② 主な出力項目
■ 概要
・決定係数$${R^2}$$:重決定R2
・自由度調整済み決定係数$${R^{*2}}$$:補正R2
・誤差項の標準誤差:標準誤差

■ 分散分析表
・総平方和:合計の変動
・回帰による平方和:回帰の変動
・残差平方和:残差の変動
・$${F}$$値:観測された分散比
・$${p}$$値:有意F

■ 回帰係数
・推定量:係数
・標準誤差:標準誤差
・$${t}$$値:t
・$${p}$$値:P-値
・回帰係数の信頼区間:下限95%、上限95%など

決定係数$${R^2=0.66}$$であり、まずまずの当てはまり具合でしょう。
回帰の有意性の検定と回帰係数の検定の両方について、$${p}$$値は有意水準$${5\%}$$を大きく下回っており、モデル全体・各回帰係数は有意だと考えられます。
③ 操作手順
■ データ分析アドインの有効化
メニューに「データ分析」が表示されない場合、データ分析のアドインを有効にする必要があります。
メニューより、「ファイル」>「オプション」を選びます。
「Excelのオプション」画面の左メニュー「アドイン」を指定します。
「Excelのオプション」画面の下部の「管理」で「Excelアドイン」を選び、「設定」ボタンをクリックします。
「アドイン」画面で「分析ツール」をチェックして、OKボタンをクリックします。
■ データ分析メニュー
メニューより、「データ」① > 「データ分析」② を選択します。

■ データ分析
「データ分析」画面で「回帰分析」③を指定してOKボタン④をクリックします。

■ 回帰分析の設定
「回帰分析」の画面で次の設定を行って、OKボタン⑪をクリックします。
・入力Y範囲⑤:目的変数のデータ範囲を指定します。
・入力X範囲⑥:説明変数のデータ範囲を指定します。
・ラベル⑦:⑤⑥にて項目名を含めてデータ範囲を指定するとラベルに使用できます。
・有意水準⑧:偏回帰係数の信頼区間を指定できます。
・一覧の出力先⑨:回帰分析結果の出力方法を指定します。
・その他⑩:適宜指定します。

■ 分析結果の調整
出力オプションで指定した場所に分析結果が出力されます。
適宜、見栄えを調整します。


(4) LINEST 関数
① 完成イメージ
「LINEST 関数」を利用して、回帰分析の統計値を表示します。
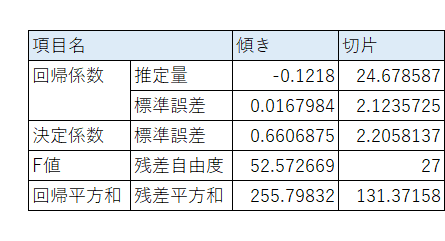
② 出力項目
出力項目は「分析ツール」と比べると限定的と言えるでしょう。
・回帰係数:推定量、標準誤差
・決定係数
・誤差項の標準誤差
・F値
・残差の自由度
・回帰による平方和
・残差平方和
※$${t}$$値、$${p}$$値は出力されないようです。
③ 操作手順
■ 枠の作成
予め枠を作ります。

■ 関数の入力
最も左上のセルに LINEST 関数の計算式を入力してENTERキーを押します。


■ ENTERキーを押した後
回帰分析の詳細統計値が該当セルに設定されます。

以上で EXCELを用いた単回帰分析の完了です。
案外、あっさりしていたのではないでしょうか。
簡単な操作であっという間に回帰分析できてしまうのがツールのいいところです。
ぜひいろんなデータで回帰分析をお試しくださいね★

2. R による単回帰分析
統計検定2級では、統計ソフトウェア「 R 」の回帰分析の出力結果が出題されます。
R を体験して、観測データと回帰分析の出力結果を見比べたり、回帰直線を描いて出力結果との関係性を確認することが、試験に出題される「出力結果」の理解の一助になる、と信じています(信念)。

(1) 2つの実行方法
この記事は次の2つの実行方法で単回帰分析を行います。
① R Studio :Rスクリプトを実行します。
② R コマンダー:プログラミング不要です。
「① R Studio」は R 言語の統合開発環境です。
プログラムを書いて自在にRの機能を操りたい方向けです。

「② R コマンダー」はメニューと画面を操作して、回帰分析の実行やグラフの表示を行う「GUI」ベースのツールです。
プログラミングが不要ですので、ユーザーの間口は広いでしょう。


(2) インストール
この記事で取り扱う2つの方法は、PC にインストールされたツールを利用します。
この節は、これからインストールをする方に向けて、インストールの概要を説明します。
既にインストール済みの方は、この節を読み飛ばしてください。
① R Studioを利用する場合
「R本体」と「R Studio」をインストールします。
「■ 参考情報」の資料を参考にしてインストールしてください。
② R コマンダーを利用する場合
「R本体」と「Rコマンダー」をインストールします。
※「R Studio」はインストールしません。
R本体のインストールは「■ 参考情報」の資料を参考にしてください。
Rコマンダーのインストールは「■ Rコマンダーのインストール」を参考にしてください。
■ 参考情報
「東京大学大学院農学生命科学研究科」様がネット公開する資料(pdf ファイル)が丁寧にインストール手順を記載していると思いますので、紹介いたします。
資料中の次の章をご覧ください。
・R本体のインストール
・RStudioのインストール
https://www.iu.a.u-tokyo.ac.jp/textbook/R/R1.010_win.pdf
■ Rコマンダーのインストール
R本体のインストール後にRコマンダーをインストールします。
① R本体を起動します。
② 「R Gui」画面より、メニュー>「パッケージ」 >「パッケージのインストール」を指定します。
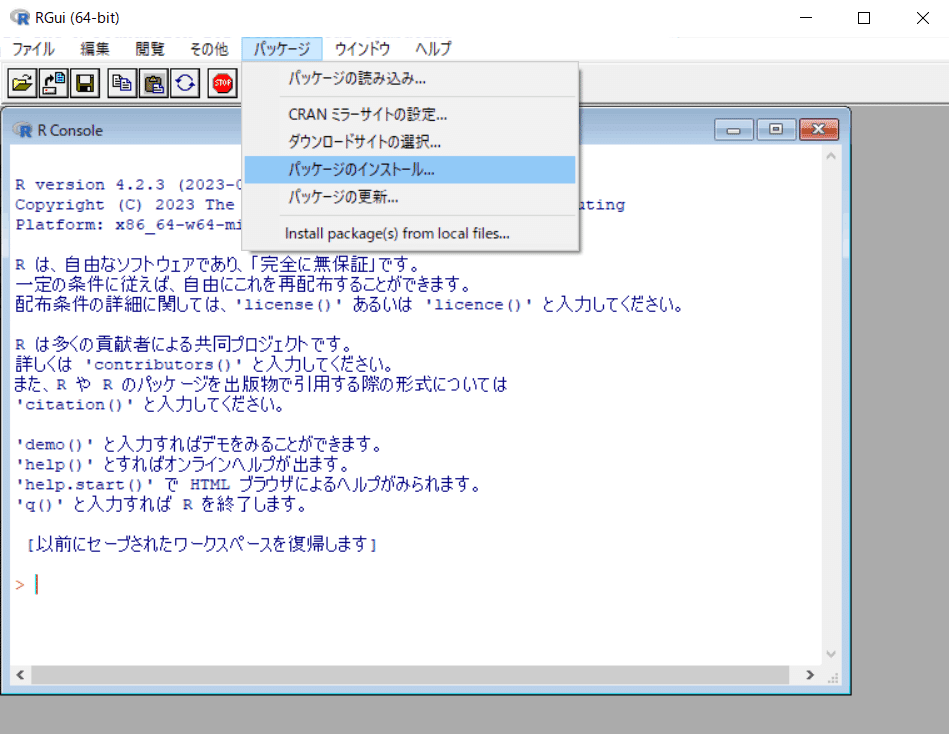
③ 「Secure CRAN mirrors」画面より「Japan(Tokyo)」を指定して「OK」ボタンをクリックします。

④ 「Packages」画面より、「Rcmdr」を指定して「OK」ボタンをクリックします。
この操作によって R コマンダーのインストールが始まります。

⑤ R コマンダーのインストールが成功すると、次の画面のように「パッケージ 'Rcmdr' は無事に展開され、MD5 サムもチェックされました」と表示されます。
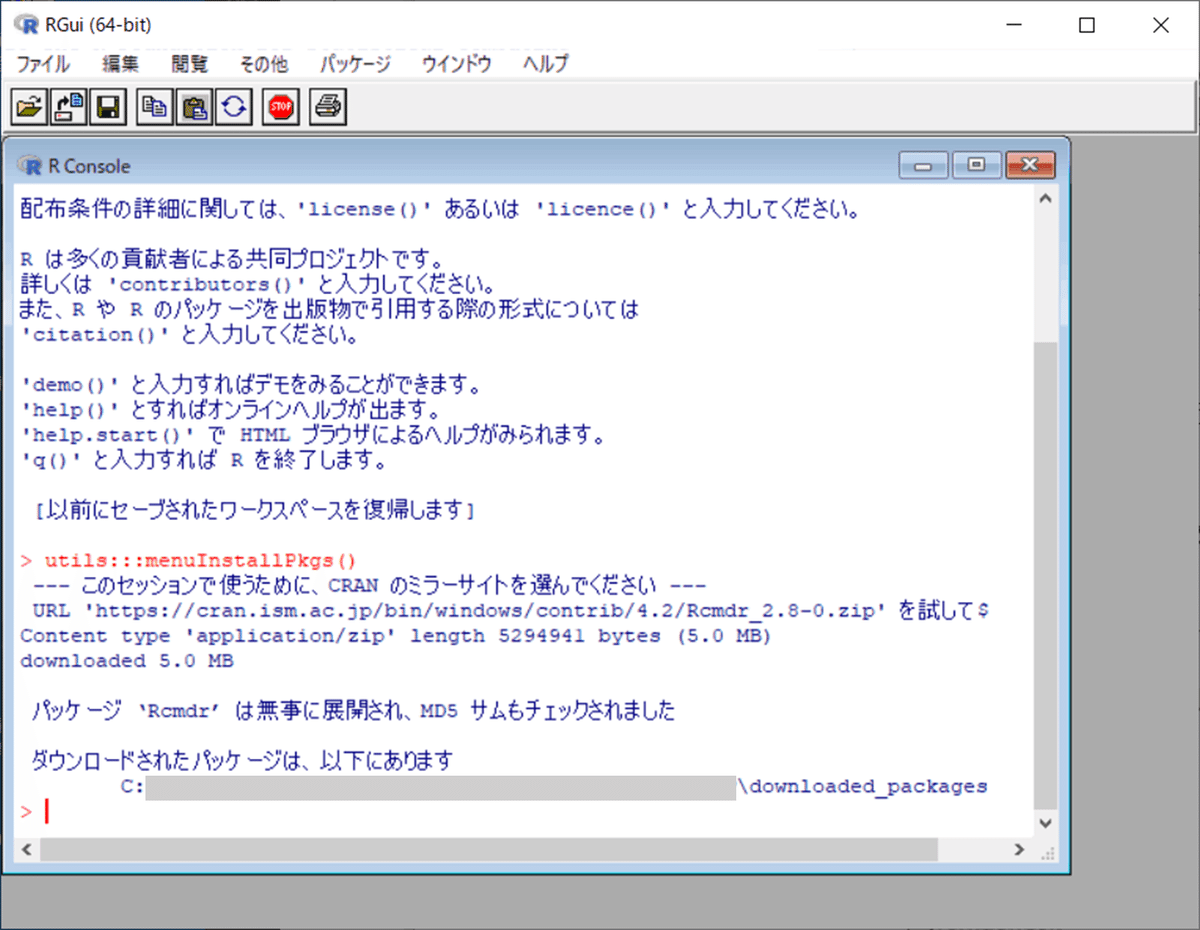
■ PCにツールをインストールしないでRを動かす方法
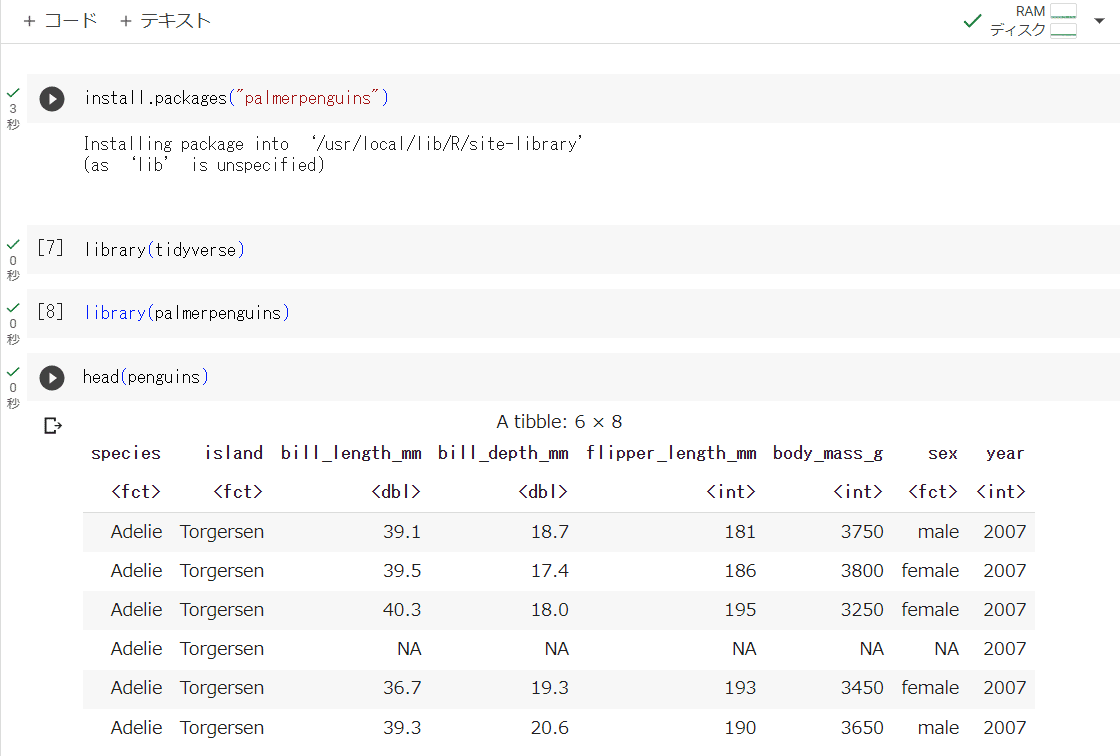
Google がブラウザで PythonやR を動かせる「Google Colab」サービスを提供しています。
PCにRをインストールをしなくても、「R Notebook」形式で R のプログラムコードを動かせます。
Google Colab で R を実行する方法の詳細はネット検索でご確認ください。
それでは R の体験ツアーのスタートです!
ぜひ楽しんでくださいね♬


(3) R Studio で単回帰分析
記事で利用する R スクリプトのサンプルファイルを共有いたします。
Rサンプルファイルのダウンロード
こちらのリンクからRスクリプト形式のサンプルファイルをダウンロードできます。
では、R Studio を起動して、単回帰分析を実践しましょう!
① 作業フォルダの設定
「sampledata.csv」ファイルを格納したフォルダを指定します。
【操作】
R Studio のメニュー>「Session」>「Set Working Directory」>「Choose Directory」を指定して開かれる「Choose Working Directory」画面でフォルダを指定します。

② R スクリプトファイルの読み込み
【操作】
R Studio のメニュー>「File」>「Open File」を指定して開かれる「Open File」画面でダウンロードした R サンプルファイルを開きます。
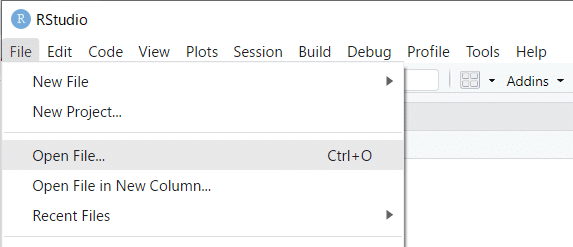
③ sampledata.csv の読み込み
この手順より、Rのコードを動かします!
まず最初に、ダウンロードした sampledata.csv (通称:コーヒーデータ)を R Studio に読み込みます。
【コード】
### データの読み込み
data <- read.csv("sampledata.csv")
# データの要約表示
str(data)
summary(data)【操作】
左上エリアのコードを1~5行目まで範囲指定して①、Runボタン②をクリックします。
この記事では、R スクリプトの実行方法をこの範囲指定&Runボタンの方式で統一します。

【コード解説】
■ data <- read.csv("sampledata.csv")
・CSV ファイルを読み込んで data に格納します。
・read.csv( "フォルダ&ファイル名" ) で CSV ファイルを開きます。
・data <- ・・・で、・・・のデータを data に格納します。
「<- 」は代入です。Pythonの = に相当します。
■ str(data)、summary(data)
・data の要約情報を表示します。
【実行結果】
左下の「Console」タブにデータの概要を表示しました。

str(data)の下の情報を見ましょう。
・data は「data.frame」(データフレーム)型です。
・data の形状は、29行、3列(変数)です。
summary(data)の下の情報を見ましょう。
・3つの変数の最小値・最大値、四分位数、平均を表示しています。
④ 相関係数の表示
【コード】
### 相関係数の計算
cor(data$世界総生産量, data$日本小売価格)【操作】
R スクリプトの7~8行目を範囲指定してRunします。

【コード解説】
■ cor(data$世界総生産量, data$日本小売価格)
・cor ( データ1, データ2 ) で相関係数を計算します。
・「data」データフレーム内の変数「世界総生産量」を指定するには、「data$世界総生産量」のように「$」で区切って指定します。
【実行結果】
左下の「Console」タブに相関係数$${-0.8128269}$$を表示しました。
目的変数「日本小売価格」と説明変数「世界総生産量」の間には、強めの負の相関関係がありました。

⑤ 回帰分析の実行
いよいよ回帰分析を実行します。
コードは至って簡潔です。R はシンプルなコードで複雑な処理を実行できるのが特徴です。
【コード】
### 回帰分析の実施と結果表示
data.lm <- lm(日本小売価格 ~ 世界総生産量, data=data)
summary(data.lm)【操作】
R スクリプトの10~12行目を範囲指定してRunします。

【コード解説】
■ data.lm <- lm(日本小売価格 ~ 世界総生産量, data=data)
・回帰分析の実行コードです(たった1行!)
・lm(日本小売価格 ~ 世界総生産量, data=data)で、data データフレームの日本小売価格を目的変数、世界総生産量を説明変数にして回帰分析を実行を指示しています。
・回帰式を「目的変数 ~ 説明変数」という書き方で指定します。
・data.lm <- で回帰分析の実行結果を data.lm に格納します。
■ summary(data.lm)
・回帰分析の実行結果を格納したdata.lmの情報を使ってサマリー情報を表示します。
このサマリー情報が統計検定2級で出題される「統計ソフトウェアの出力結果」です。
【実行結果】
左下の「Console」タブに「統計ソフトウェアの出力結果」を得ることができました。
残差の四分位情報「Residuals」、回帰係数の分析情報「coefficients」、モデル全体の分析情報の3つのゾーンで構成されています。
各項目の読み方は【第1部】でご確認ください。

【回帰分析の要約】
回帰式は$${y=24.6786-0.1218x}$$です。
回帰係数の$${p}$$値(Pr(>| t |))は極小であり、有意水準$${5\%}$$で回帰係数は0でないと言えます。
決定係数$${R^2}$$は$${0.6607}$$です。モデルの当てはまり具合はまあまあでしょう。
$${F}$$値は$${52.57}$$、$${p}$$値は極小です。有意水準$${5\%}$$で回帰係数のどれかが0ではないと言えます。
残差の自由度は$${27=29-1-1}$$、標準誤差(Residual standard error)は$${2.206}$$です。
⑥ 回帰直線のグラフ描画
回帰分析の実行結果を格納した data.lm を用いて、回帰直線を描画しましょう。
【コード】
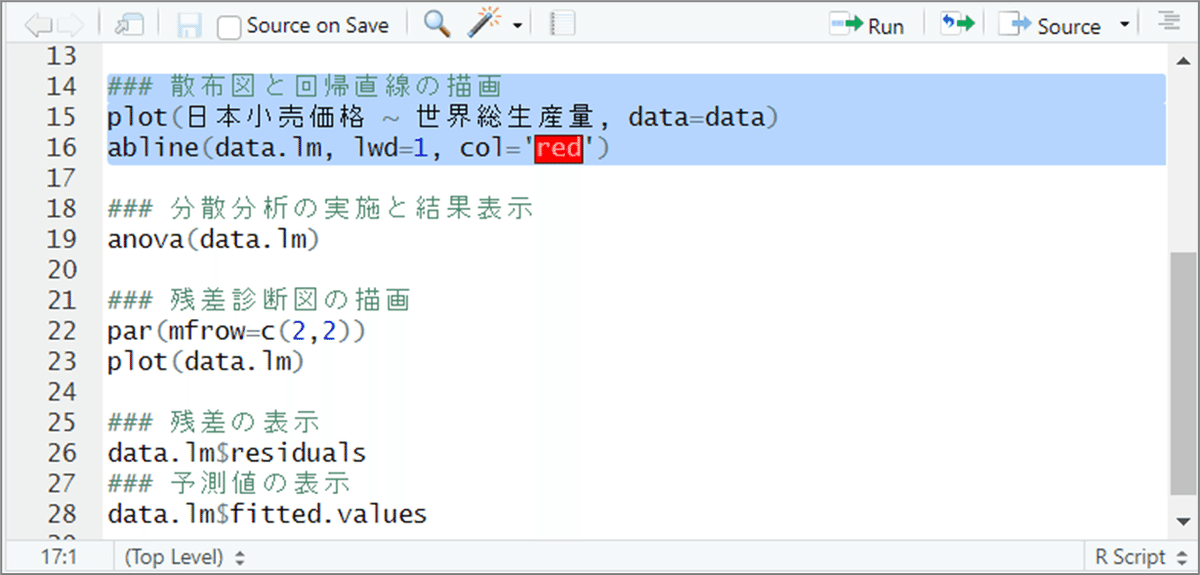
### 散布図と回帰直線の描画
plot(日本小売価格 ~ 世界総生産量, data=data)
abline(data.lm, lwd=1, col='red')【操作】
R スクリプトの14~16行目を範囲指定してRunします。
【コード解説】
■ plot(日本小売価格 ~ 世界総生産量, data=data)
・散布図を描画します。
・引数に、data データフレームの日本小売価格を目的変数、世界総生産量を説明変数を指定しています。
・「目的変数 ~ 説明変数」という書き方で指定します。
■ abline(data.lm, lwd=1, col='red')
・直線を描画します。
・回帰分析の実行結果を格納した data.lmを指定します。
・線の幅を lwd=1 で、線の色を col='red' (赤色)で指定します。
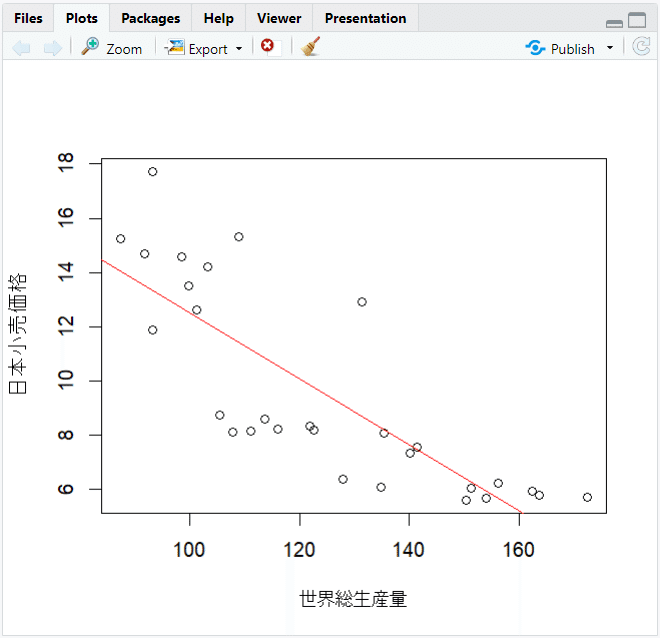
【実行結果】
右下エリアに散布図と回帰直線のグラフが表示されました。
⑦ 分散分析の実行
回帰分析の結果を利用して分散分析表を作成しましょう。
1行です。
【コード】
### 分散分析の実施と結果表示
anova(data.lm)【操作】
R スクリプトの10~12行目を範囲指定してRunします。

【コード解説】
■ anova(data.lm)
・anova()で分散分析を行って分散分析表を出力します。
・anova()に与えるデータは、回帰分析の結果を格納した data.lm です。
【実行結果】
説明変数「世界総生産量」と残差(Residuals)の2行が表示されています。
列の項目は、自由度(Df)、平方和(Sum Sq)、平均平方(Mean Sq)、$${F}$$値(F value)、$${p}$$値(Pr(>F))です。
$${F}$$値と$${p}$$値は、回帰分析の結果の同値と一致しています。

⑧(参考)残差診断図のグラフ描画
【第1部】で紹介した「残差診断で用いるプロット」を R で表示してみましょう。
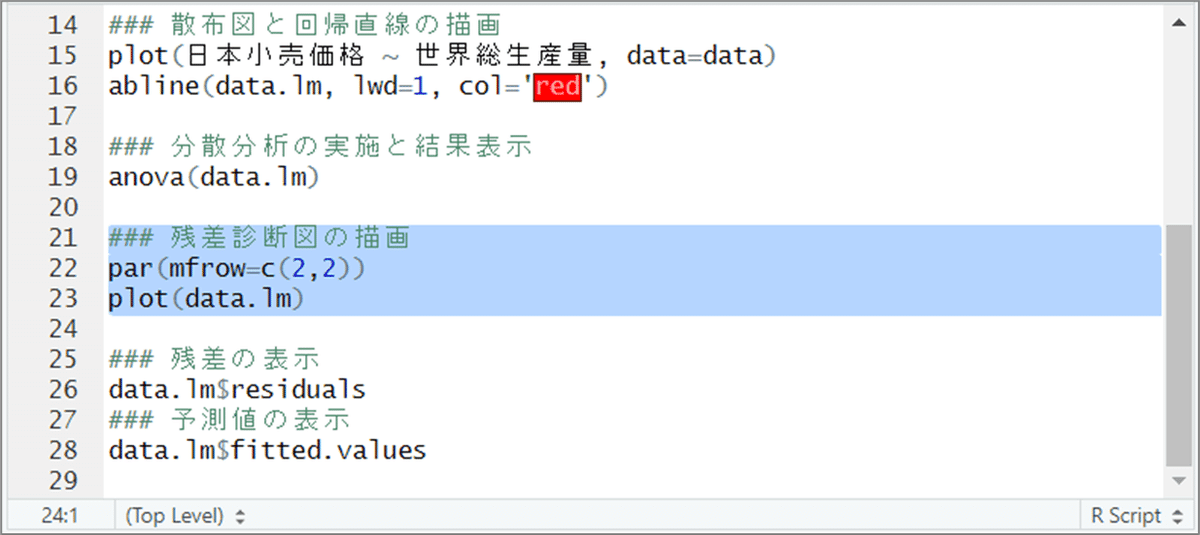
【コード】
### 残差診断図の描画
par(mfrow=c(2,2))
plot(data.lm)【操作】
R スクリプトの21~23行目を範囲指定してRunします。
【実行結果】
右下エリアに残差診断図の4つのグラフが表示されました。
等分散性、独立性、正規性、外れ値の観点で大きな問題はなさそうな感じです。

⑨ (参考)回帰分析結果データの表示
回帰分析の実行結果を格納した data.lm から、残差データと予測値データを取り出してみましょう。
【コード】
### 残差の表示
data.lm$residuals
### 予測値の表示
data.lm$fitted.values【操作】
R スクリプトの25~28行目を範囲指定してRunします。

【コード解説】
・残差と予測値は、回帰分析の実行結果を格納した data.lm の中の変数「residuals」、「fitted.values」に格納されています。
【実行結果】
左下の「Console」タブに目的変数の残差(=観測値-予測値)と予測値がそれぞれ 標本サイズの 29 づつ表示されました。

⑩ その他~読み込んだデータの表示
CSV ファイルを読み込んで作成した data の内容を表示します。
【操作】
右上エリアの「data」をクリックします。

【実行結果】
左上エリアに「data」タブが追加されました。
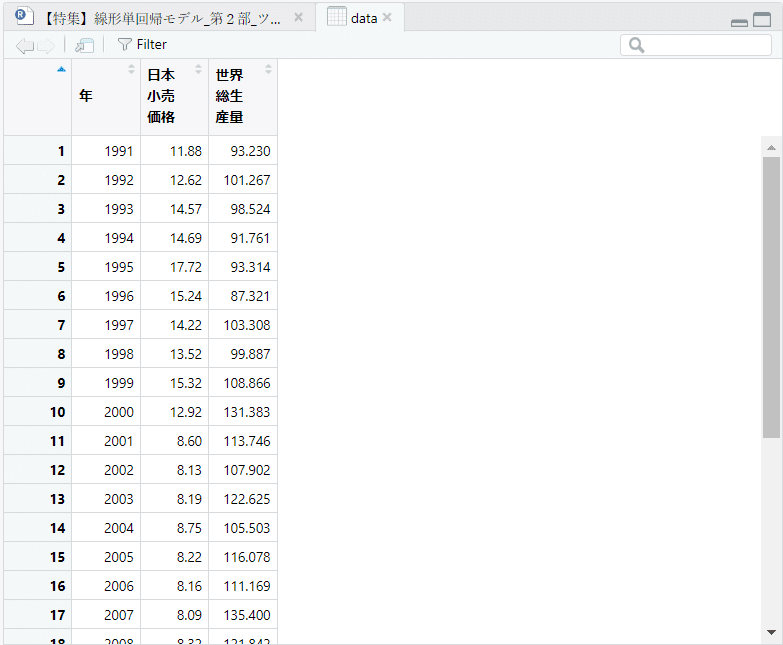
以上で R Studio を用いた単回帰分析の完了です。
「統計ソフトウェアの出力結果」は次の3ステップでサクッと表示できることが分かりました。
・read.csv()の1行で CSV ファイルを読み込み
・lm()の1行で回帰分析を実行
・summary()の1行で結果を出力
お手元のデータを利用して、R の回帰分析をガンガン試してみましょう!

(4) R コマンダーで単回帰分析
① R コマンダーの起動
R 本体の「R Gui」から R コマンダーを起動します。
※予め R 本体の「R Gui」を起動しておいてください。
【操作】
「R Gui」のメニューより、「パッケージ」>「パッケージの読み込み」を指定します。

「Select one」画面より、「Rcmdr」を選択してOKボタンを押します。
【実行結果】
「R コマンダー」画面が開きました。

② sampledata.csv の読み込み
【操作】
「R コマンダー」のメニューより、「データ」>「データのインポート」>「テキストファイルまたはクリップボード, URLから」を指定します。

「ファイルまたはクリップボード, ・・・」画面が開きます。
「フィルドの区切り記号」の「カンマ」をオンにして、OKボタンを押します。
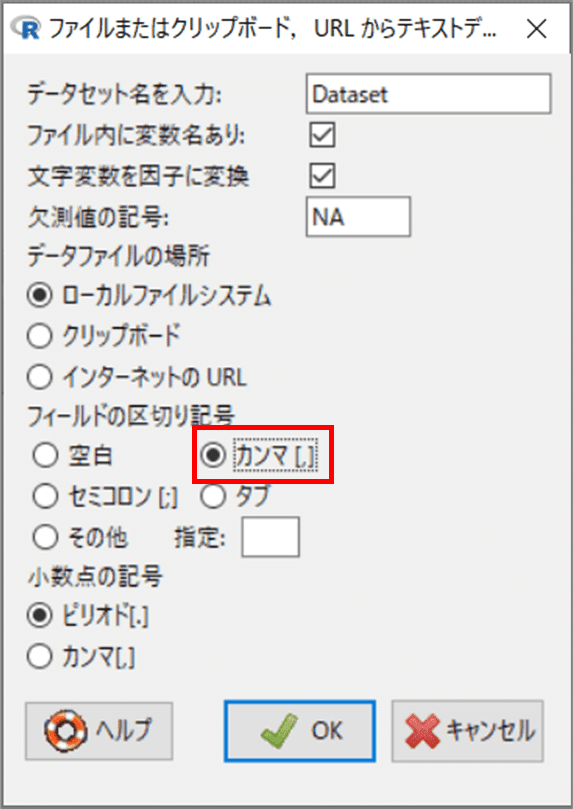
「開く」画面で「sampledata.csv」を選択して、ファイルを開きます。
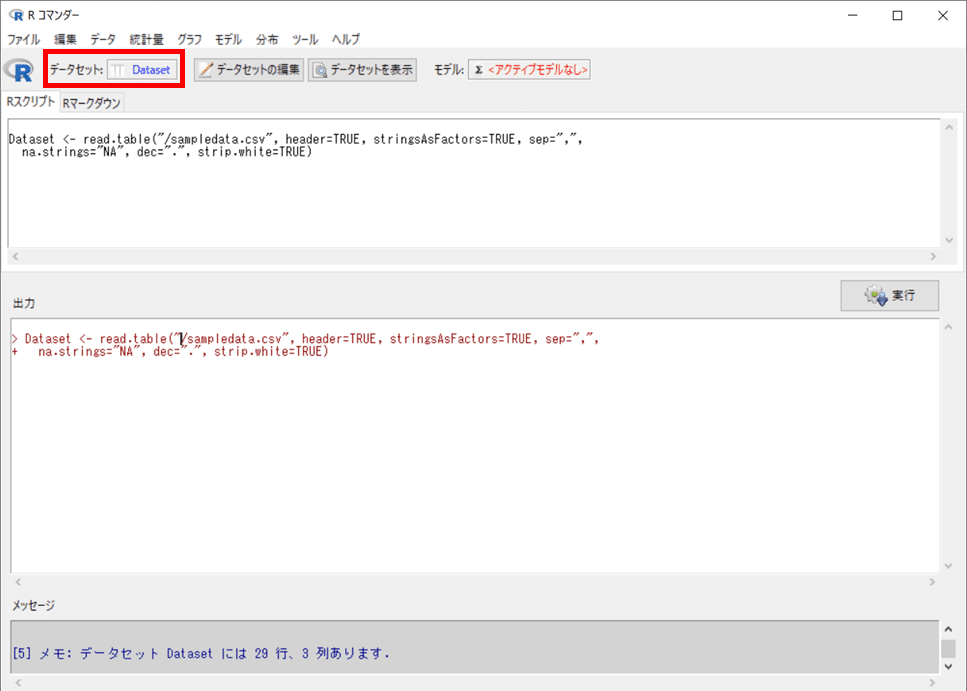
ファイルを開いた後の「R コマンダー」の画面は次のようなイメージになります。
「データセット」の表示エリアに「Dataset」と表示されました。
先程 CSVファイルを読み込む際に、データセット名を「Dataset」(デフォルト表示値)としています。
R コマンダーに無事、データセット:Dataset が読み込まれて、アクティブになっていることが分かりました。
③ 読み込んだデータの表示
【操作】
「R コマンダー」の「データセットを表示」ボタンをクリックします。

【実行結果】
「Dataset」画面が開きました。
読み込んだ CSV ファイルには、「年」「日本小売価格」「世界総生産量」の3変数があることが分かります。
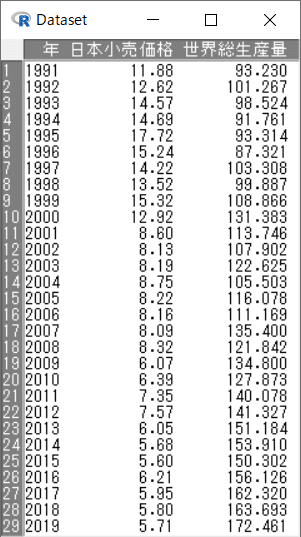
④ 要約統計量の表示
【操作】
「R コマンダー」のメニューより、「統計量」>「要約」>「アクティブデータセット」を指定します。
【実行結果】
「R コマンダー」下部の「出力」エリアに「summary」が表示されました。
最小値、最大値、四分位数、平均値です。

⑤ 相関係数の表示
【操作】
「R コマンダー」のメニューより、「統計量」>「要約」>「相関行列」を指定します。

「相関行列」画面で次のとおり指定して、OKボタンをクリックします。
・変数:「世界総生産量」と「日本小売価格」を選択
・相関のタイプ:ピアソンの積率相関を選択
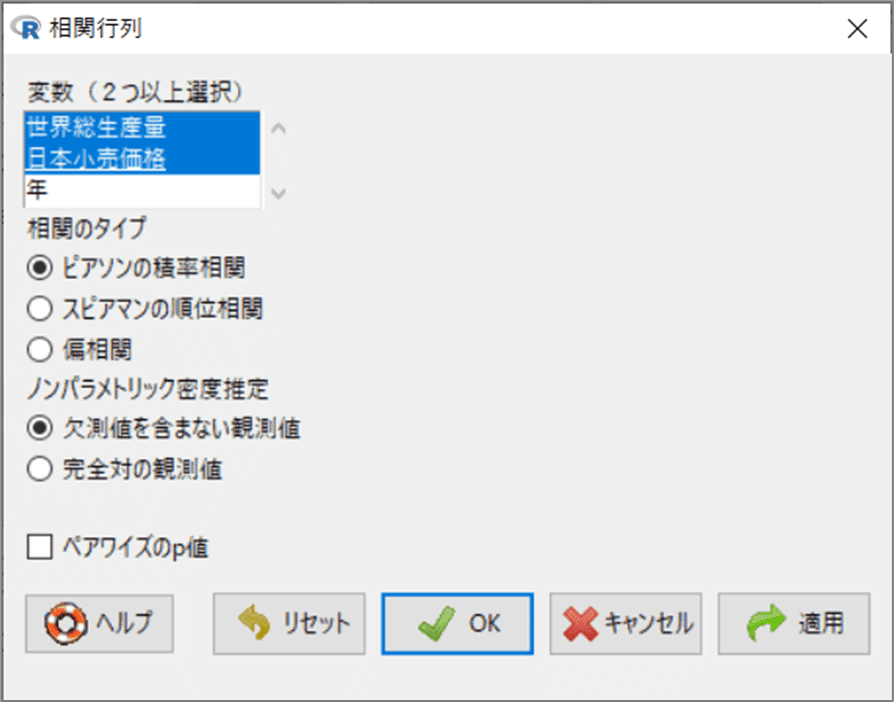
【実行結果】
「R コマンダー」の「出力」エリアに相関行列が表示されました。
世界総生産量と日本小売価格の相関係数は$${-0.8128269}$$です。
2つの変数の間には強めの負の相関関係があります。

⑥ 回帰分析の実行
【操作】
「R コマンダー」のメニューより、「統計量」>「モデルへの適合」>「線形回帰」を指定します。
「線形回帰」画面で次のとおり指定して、OKボタンをクリックします。
・目的変数:「日本小売価格」を選択
・説明変数:「世界総生産量」を選択

【実行結果】
「R コマンダー」の「出力」エリアに回帰分析結果が表示されました。
統計検定2級の問題でおなじみの「統計ソフトウェアの出力結果」です。
残差の四分位情報「Residuals」、回帰係数の分析情報「coefficients」、モデル全体の分析情報の3つのゾーンで構成されています。
各項目の読み方は【第1部】でご確認ください。

⑦ 回帰直線のグラフ描画
【操作】
「R コマンダー」のメニューより、「グラフ」>「散布図」を指定します。

「散布図」画面の「データ」タブで次のとおり指定して、「オプション」タブをクリックします。
・x変数:「世界総生産量」を選択
・y変数:「日本小売価格」を選択

「散布図」画面の「オプション」タブで次のとおり指定して、OKボタンをクリックします。
・最小2乗直線を選択

【実行結果】
「R Gui」画面に変わります。
「R Graphics」画面に、散布図と回帰直線のグラフが表示されました。

⑧ 分散分析の実行
【操作】
「R コマンダー」のメニューより、「モデル」>「仮説検定」>「分散分析表」を指定します。
「分散分析表」画面で次のとおり指定して、OKボタンをクリックします。
・検定のタイプ:「逐次的平方和("Type I")」を選択

【実行結果】
「R コマンダー」の「出力」エリアに分散分析表が表示されました。
説明変数「世界総生産量」と残差(Residuals)の2行が表示されています。
列の項目は、自由度(Df)、平方和(Sum Sq)、平均平方(Mean Sq)、$${F}$$値(F value)、$${p}$$値(Pr(>F))です。
$${F}$$値と$${p}$$値は、回帰分析の結果の同値と一致しています。

⑨ (参考)残差診断図のグラフ描画
【第1部】で紹介した「残差診断で用いるプロット」を表示してみましょう。
【操作】
「R コマンダー」のメニューより、「モデル」>「グラフ」>「基本的診断プロット」を指定します。
【実行結果】
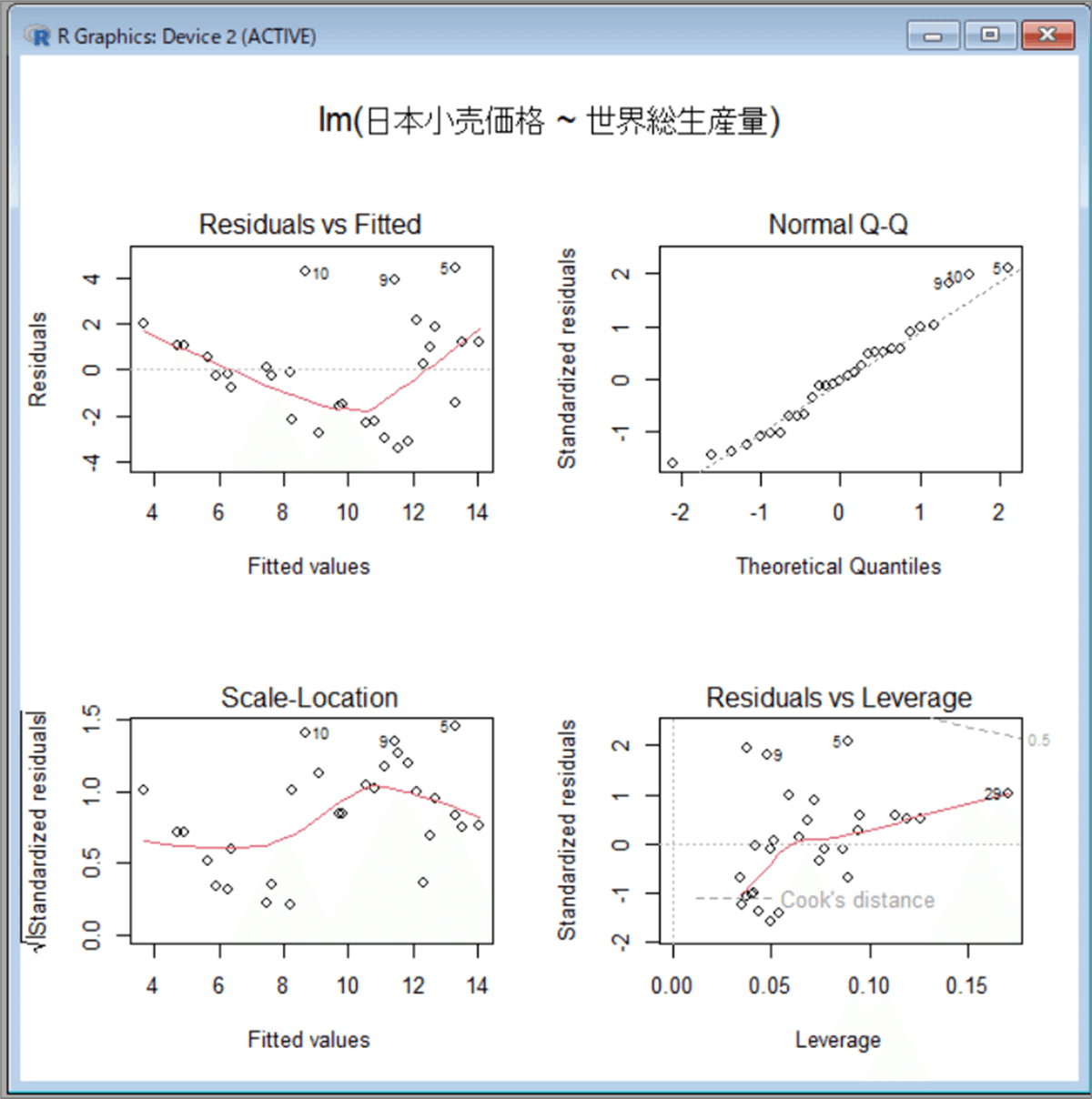
「R Gui」画面に変わります。
「R Graphics」画面に、基本的診断プロットの4つのグラフが表示されました。
⑩ (参考)R コマンダーの画面操作から R スクリプトを学ぶ
「R コマンダー」の「Rスクリプト」タブをご覧ください。
画面から実行した処理のコードが表示されています。
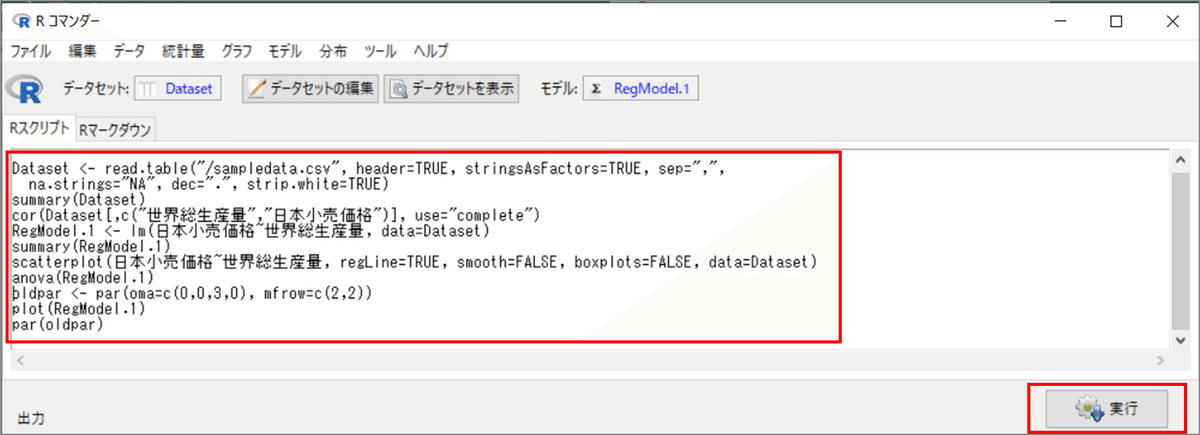
実は、R コマンダーの各画面はOKボタンのクリックなどで処理を実行する時、この「R スクリプト」タブに「R スクリプト」(コード)を記録しているのです。
「R スクリプト」タブのコードを範囲指定して、右下の「実行」ボタンをクリックすると、当該コードを実行できます。
また、R スクリプトをファイル保存することもできます。
-メニュー>「ファイル」>「スクリプトに名前をつけて保存」
画面操作をしながら、R スクリプトも学べるのです!
ぜひご活用ください。
以上で R コマンダーを用いた単回帰分析の完了です。
画面操作だけで「プログラミング無しで」データ分析ができる R コマンダーをぜひご活用ください。

(5) R コマンダー関連情報
① 入門書の紹介
「統計ソフト「R」超入門〈最新版〉 統計学とデータ処理の基礎が一度に身につく! (ブルーバックス)」
サンプルデータと R コマンダーの主要画面を使って、データ分析のイロハを実践的に学べる良書です。
ブルーバックスサイズなので「ハンドブック」としても重宝します。

② 機能拡張アプリの紹介
R コマンダーに機能を追加するアプリが2つあります。
主に医療研究で使われる統計手法を追加できるそうです。
詳しい情報は次のサイトを訪問してご確認ください。
1️⃣ EZR(Easy R)
2️⃣ 改変Rコマンダー
3. Python による単回帰分析
(1) Pythonの主要な回帰分析ライブラリ
この記事は「statsmodels.formula.api」を用いて回帰分析を実行します。
Pythonには多くの回帰分析ライブラリが存在するようです。
私の調べた範囲では、次の5種類が見つかりました。
① statsmodels:formula.api の ols 関数
② statsmodels:api の OLS 関数
③ scipy.stats:linregress 関数
④ pingouin:linear_regression 関数
⑤ scilit-learn:LinearRegression クラス
これらの中から、統計検定2級に出題される「統計ソフトウェアの出力結果」に近いアウトプットを作成できて、分散分析に連動できる「① statsmodels の formula.api の ols 関数」を選びました。
その他のライブラリのコード例は、Pythonサンプルファイルに付属する「おまけコード」をご参照ください。
また、この記事は以下の想定の下で、Pythonを動かします。
Jupyter Notebookを用いてPythonを動かします。
すでに Jupyter Notebook を使える PC 環境が整っていることを想定します。
■ Python をインストールする場合のご案内
Pythonのインストールから始める場合は、たとえば次のリンクのサイトの「1. Anacondaと一緒にJupyter Notebookもインストールする方法(Windows・Mac)」などをご参照いただき、インストールを進めてください。
記事で利用する Python コードのサンプルファイルを共有いたします。
Pythonサンプルファイルのダウンロード
こちらのリンクからJupyter Notebook形式のサンプルファイルをダウンロードできます。
それでは Python の旅に出発しましょう!


(2) statsmodels で単回帰分析
① インポート
【コード】
### インポート
# 数値計算
import numpy as np
import pandas as pd
# 統計処理
import statsmodels.api as sm
import statsmodels.formula.api as smf
import lmdiag
# 可視化
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'Meiryo'【実行結果】
特になし
② sampledata.csvの読み込み
まず最初に、ダウンロードした sampledata.csv (通称:コーヒーデータ)を pandas のデータフレーム「data」に読み込んで、データの形状と先頭5行を表示します。
【コード】
### sampledata.csvの読み込み
# csvファイルの読み込み
data = pd.read_csv(r'sampledata.csv', index_col=0)
# 形状、先頭5行の表示
print('data.shape', data.shape)
display(data.head())【実行結果】

コーヒーデータは、行数29, 列数2 の形状です。
目的変数は日本小売価格、説明変数は世界総生産量です。
「年」はインデックスです。
read_csv()関数の引数 index_col=0 で0番目の列=最左列をインデックスに指定しています。
③ 要約統計量の表示
pandas の describe を用いて要約統計量を表示します。
【コード】
### 要約統計量の表示
data.describe()【実行結果】
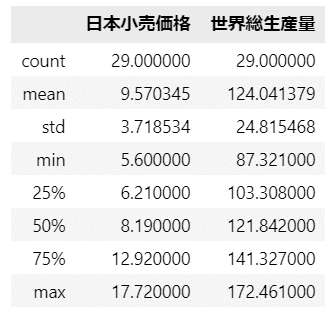
データ件数、平均値、標準偏差、最小値・最大値、四分位数が表示されました。
④ 相関係数の表示
pandas の corr()関数を用いて、相関行列を表示します。
### 相関係数の表示
data.corr()【出力結果】

世界総生産量と日本小売価格の相関係数は$${-0.812827}$$です。
強めの負の相関関係があります。
⑤ 回帰分析の実行
いよいよ回帰分析の実行のときが来ました。
statsmodels.formula.api の ols() 関数を利用します。
### 回帰分析の実行
# 回帰モデルの定義
model = smf.ols('日本小売価格 ~ 世界総生産量', data=data)
# 回帰分析の実行
result = model.fit()
# サマリーの表示
result.summary()【コード解説】
■ model = smf.ols('日本小売価格 ~ 世界総生産量', data=data)
・回帰モデルを定義しています。
・smf.ols() の最初の引数は ' 日本小売価格 ~ 世界総生産量'。
「目的変数 ~ 世界総生産量」の式の書き方が R の lm関数と似ています。
・smf.ols() の2つ目の引数は pandasのデータフレームです。
■ result = model.fit()
・fit() メソッドで回帰分析を実行しています。
・回帰分析の結果を変数 result に格納します。
■ result.summary()
・summary()メソッドで回帰分析の結果のサマリーを表示します。
【実行結果】
とても沢山の数値が表示されました。

上段と下段に分けて確認しましょう。
上段のテーブルには、モデル全体にかかるデータが表示されます。
決定係数$${R^2}$$は0.661。まあまあの当てはまり具合です。
$${F}$$値の$${p}$$値は$${0.000}$$。回帰係数のどれかは0では無いと言えます。

下段のテーブルの上部には、回帰係数にかかるデータが表示されます。
切片(Intercept)、傾き(説明変数:世界総生産量)の回帰係数より、回帰式は$${y=24.6786-0.1218x}$$です。
2つの係数の$${p}$$値は$${0.00}$$です。回帰係数は0で無いと言えるでしょう。

⑥ 誤差項の標準誤差の表示
「統計ソフトウェアの出力結果」に含まれる「誤差項の標準誤差」を表示します。
回帰分析の結果 result に格納された分散の推定値「mse_resid」の平方根を計算します。
【コード】
### 誤差項の標準誤差の表示
print(f'誤差項の標準誤差: {np.sqrt(result.mse_resid):8.4f}')【実行結果】

⑦ 回帰直線のグラフ描画
pandas の 散布図描画機能 plot.scatter を用いて散布図を描画します。
その上に、matplotlib.pyplot の plot機能を用いて回帰直線を描画します。
回帰直線に用いる目的変数の予測値は、回帰分析の結果 result に格納された予測値「fittedvalues」を利用します。
【コード】
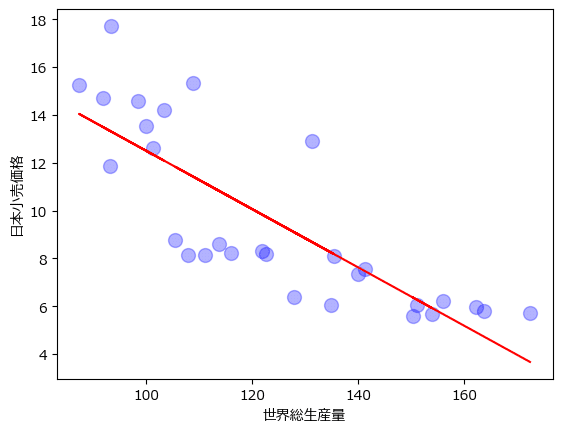
### 回帰直線のグラフ描画
# 散布図の描画
data.plot.scatter(x='世界総生産量', y='日本小売価格', s=100, color='b', alpha=0.3)
# 回帰直線の描画
plt.plot(data['世界総生産量'], result.fittedvalues, 'r');【実行結果】
⑧ 分散分析の実行
回帰分析の結果 result を利用して分散分析表を作成しましょう。
statsmodels.api の anova.lm 関数に result を引数にして実行します。
【コード】
### 分散分析の実行
sm.stats.anova_lm(result).round(4)【実行結果】
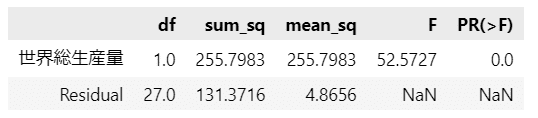
分散分析表を表示できました。
列名は左から、自由度、平方和、平均平方、$${F}$$値、$${p}$$値です。
⑨ (参考)残差診断図のグラフ描画
R で作成した残差診断図をPythonで描画します。
「lmdiag」というパッケージを用いて描画します。
必要に応じて pip でインストールしてください。
### lmdiagのインストールコマンド
pip install lmdiagstatsmodels.formula.api の回帰分析出力結果 result を用いて、lmdiag で4つの残差診断図を作成します。
【コード】
### (参考)残差診断図のグラフ描画
plt.figure(figsize=(7, 7))
lmdiag.plot(result);【実行結果】

⑩ (参考)回帰分析結果データの表示
回帰分析の結果 result に格納された残差 resid と予測値 fittedvalues を表示します。
pandas のデータフレーム化をして見栄えを整えました。
まずは残差から。先頭5行を表示します。
【コード】
### 残差の表示
display(pd.DataFrame(result.resid, columns=['残差']).head())【実行結果】

続いて予測値。先頭5行を表示します。
【コード】
### 目的変数の予測値の表示
display(pd.DataFrame(result.fittedvalues, columns=['予測値']).head())【実行結果】
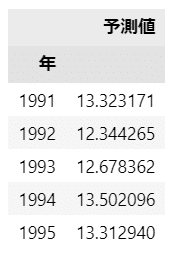
以上で Pythonを用いた単回帰分析の完了です。
Python も R と同様に、短いコードで回帰分析を実行できます。
ぜひお手元のデータでバンバン回帰分析を試してみてくださいね。

4. 追加:フリーの統計ソフトウェアによる単回帰分析
(1) フリーの統計ソフトウェアの使い心地を試す
ツールの比較にあたって、「統計専用ツール」を対象にしたくなりました。
そこで、「無料」「インストールが簡単」「操作しやすい」の点で、『College Analysis』を使ってみることにしました。
次のリンクは College Analysis のサイトです。
このサイトの「College Analysis 最新版のダウンロード」の最新版ZIPファイルをダウンロードして解凍すると、College Analysis を利用できるようになります。
また「マニュアルのダウンロード」でマニュアルをダウンロードできます。

(2) College Analysis による単回帰分析
College Analysis を「CA」と短縮表記します。
【利用バージョンについて】
この記事は、CA のバージョン 8.8 を利用しています。
最新バージョンとメニューが異なる可能性があります。
CA 用のCSVファイルのダウンロード
こちらのリンクから CA 用のCSVファイルをダウンロードできます。
※冒頭のCSVファイルの文字コードをSHIFT-JISに変更したものです。
① sampledata_ca.csv の読み込み
【操作】
「CA」のメニューより、「ファイル」>「開く」を指定します。

「開く」画面が開きます。
sampledata_ca.csvファイルを指定します。
※開く画面の画面イメージは省略します。
「CAnalysis」画面の「はい」ボタンをクリックします。

「QInput」画面の区切り文字が「,」(カンマ)になっていることを確認してOKボタンをクリックします。
【実行結果】
「データ編集」画面にコーヒーデータが読み込まれました。

② 回帰分析の実行
早速、回帰分析しましょう!
【操作】
「CA」のメニューより、「分析」>「多変量解析他」>「予測手法」>「重回帰分析」を指定します。
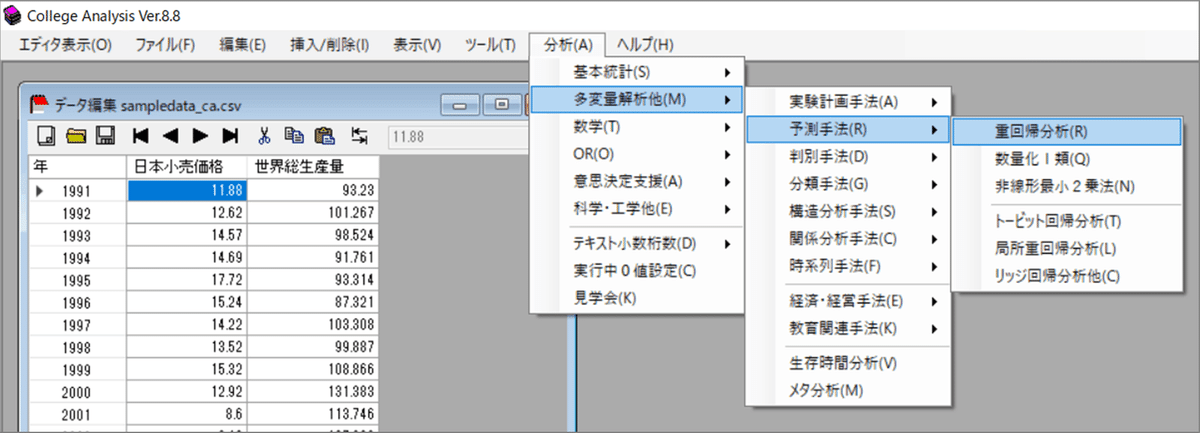
「多変量解析」画面の「変数選択」ボタンをクリックします。

「変数選択」画面で「All」ボタンをクリックします。
下の白い枠に2つの変数が表示されます。
目的変数の「日本小売価格」が上になっていることを確認して、OKボタンをクリックします。

「多変量解析」画面に戻ります。
さあ、重回帰分析を実行しましょう!
「重回帰分析」ボタンをクリックします。
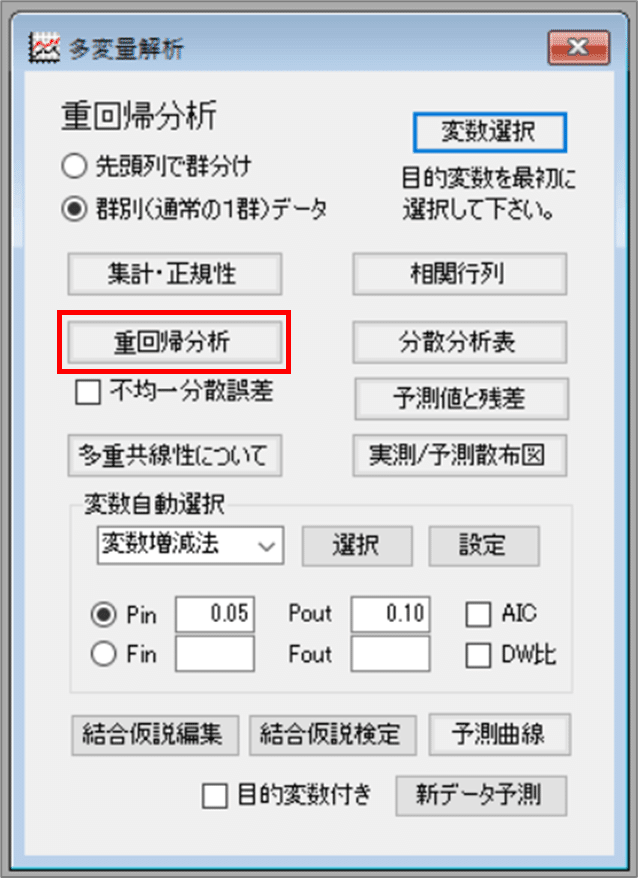
【実行結果】
2つの画面が表示されました。
まずは横長の「偏回帰係数と検定」画面から。
上の2行が回帰係数、下の2行がモデル全体の評価指標です。

回帰係数の項目は左から、「回帰係数の推定値」「データを標準化したときの回帰係数の推定値」、「回帰係数の標準誤差」、「$${t}$$値」、「自由度」、「$${p}$$値」、回帰係数の95%信頼区間「下限」と「上限」、「相関係数」、「偏相関係数」です。
モデル全体の評価指標は左から、「重相関係数$${R}$$」、「決定係数$${R^2}$$」、「自由度調整済み決定係数$${R^{*2}}$$」、「$${F}$$値」、「$${p}$$値」です。
統計検定2級の「統計ソフトウェアの出力結果」がほぼ揃っています!
(誤差項の標準誤差のみ未表示)
次の「重回帰分析」画面は、回帰分析のサマリー、残差の正規性の検定、回帰の有意性の検定($${F}$$検定)の結果、情報量規準AIC、DW比(自己相関のチェック)を表示しています。
なんでしょう、回帰分析がいい感じに進んでいる感じがします。

③ 分散分析の実行
続けて分散分析を実行しましょう。
メニューが1つにまとまっているので使いやすいです。
【操作】
「多変量解析」画面の「分散分析表」ボタンをクリックします。
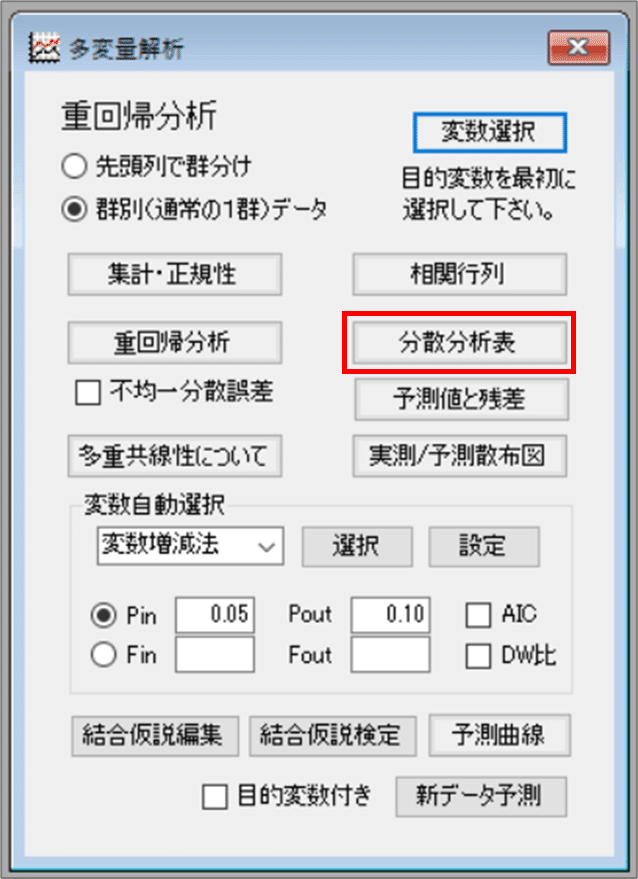
【実行結果】
「分散分析表」画面が開きました。
全変動=総平方和、回帰変動=回帰による平方和、残差変動=残差平方和と読み替えましょう。
総平方和が1行目に位置するなど、行の並びに少々違和感がありますが、分散分析表の項目を網羅しています。

④ 回帰直線のグラフ描画
【操作】
「CA」のメニューより、「分析」>「基本統計」>「集計グラフ」>「2次元グラフ」を指定します。
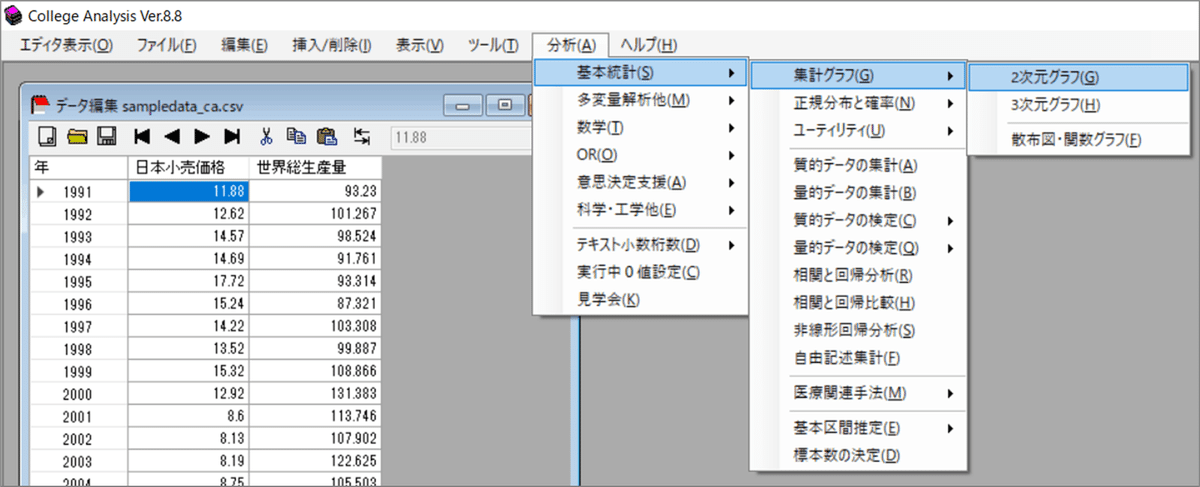
「基本統計」画面の「グラフ選択」で「散布図」指定して、「実行」ボタンをクリックします。

【実行結果】
回帰直線が描画された散布図のグラフを表示しました。

⑤ (参考)回帰分析結果データの表示
目的変数の予測値と残差を表示します。
【操作】
「多変量解析」画面の「予測値と残差」ボタンをクリックします。

【実行結果】
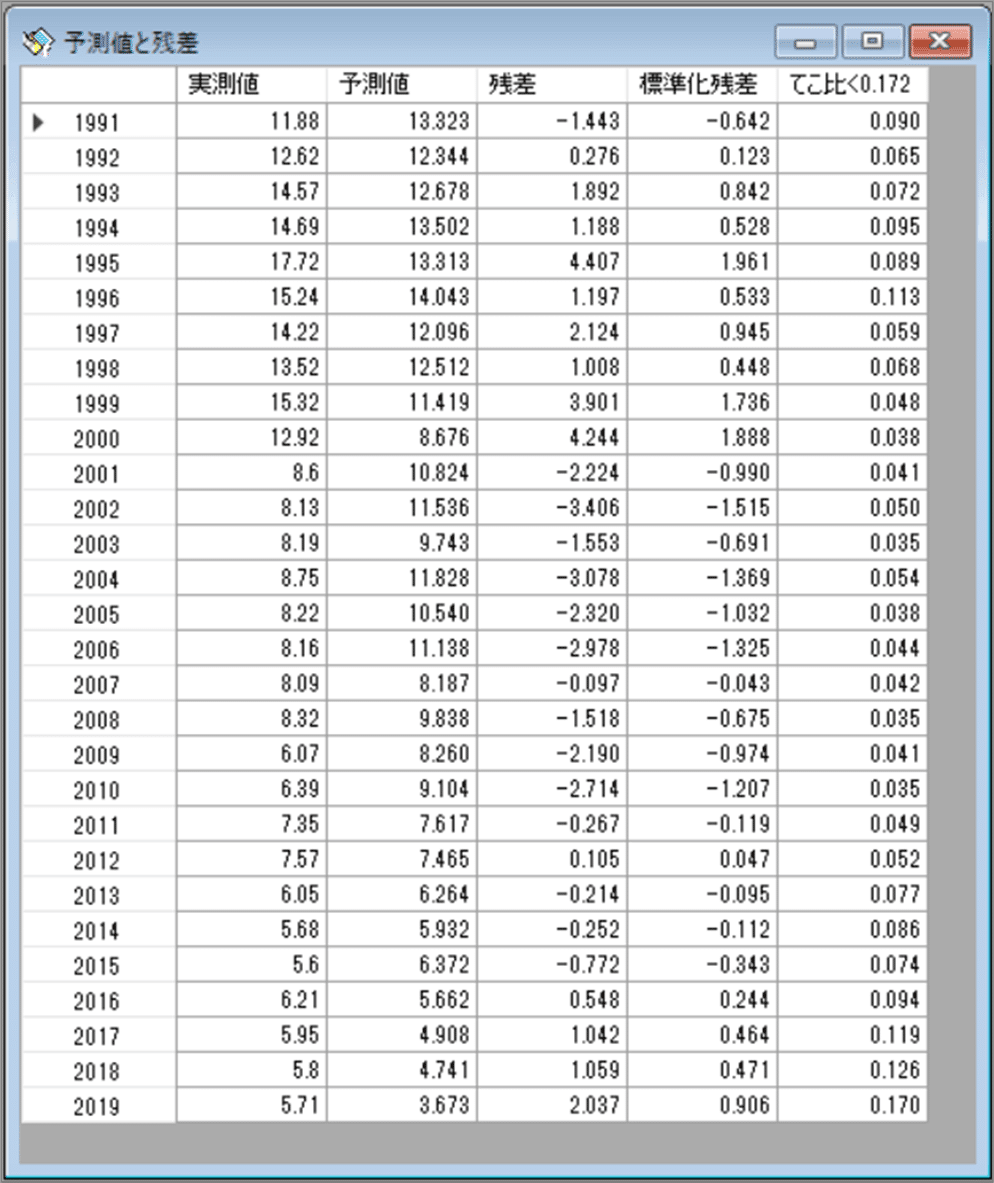
「予測値と残差」画面が開きました。
観測値、予測値、残差などを確認できました。
⑥ (参考)残差診断図のグラフ描画
※該当機能を見つけられませんでした。
■ 分析データの活用方法
実行結果の表やテキストのデータはコピーして、EXCELやテキストファイルに貼り付けして活用します。
以上で College Analysis を用いた単回帰分析の完了です。
統計・データ分析専用のソフトウェアなので、機能の充実度が高く、操作しやすい印象です。
使い勝手を試してみてくださいね。

5. 比較表
この記事で取り上げた5つのツールを簡単に比較してみます。
■ 始めるときのハードルの高さ
$$
\begin{array}{c:cc}
ツール & ソフト代金 & プログラミング\\
\hline
\text{EXCEL} & 有償 & なし\\
\text{R Studio} & フリー & 必要\\
\text{Rコマンダー} & フリー & なし\\
\text{Python} & フリー & 必要\\
\text{CA} & フリー & なし\\
\end{array}
$$

■ 統計・データ分析機能の充実度
$$
\begin{array}{c:cc}
ツール & 統計機能全般 & 統計専用画面 & データ分析全般\\
\hline
\text{EXCEL} & 限定的 & まあまあ & まあまあ\\
\text{R Studio} & とても充実 & なし & 充実\\
\text{Rコマンダー} & 限定的 & 充実 & 限定的\\
\text{Python} & 充実 & なし & とても充実\\
\text{CA} & 充実 & 充実 & 充実\\
\end{array}
$$

■ 使いやすさ・調べやすさ
$$
\begin{array}{c:cc}
ツール & 操作で使う言語 & ネット情報量\\
\hline
\text{EXCEL} & 日本語 & 多い\\
\text{R Studio} & 英語 & 中程度\\
\text{Rコマンダー} & ほぼ日本語 & 少ない\\
\text{Python} & 英語 &多い\\
\text{CA} & 日本語 & 少ない\\
\end{array}
$$

【所感】
EXCELは使い勝手はいいのですが、有償です。
個人利用の場合、導入のハードルが高く感じるかもしれません。その他のツールは、プログラミングの要否、使いやすさ、統計・データ分析機能の充実度、情報収集のしやすさの観点で、お好みのツールをお使いいただくのがいいかと思います。
プログラミングOK → Python、R
統計分野でガンガンとデータ分析 → R
機械学習分野でバンバンとデータ分析 → Python
プログラミングNG → R コマンダー、CA
今後、統計分野でデータ分析する予定 → R コマンダー
ひとまずお試し → CA
意外にCA (Collage Analysis)は導入しやすいツールになりそうです。
みなさんにとって最適なツールが見つかるといいですね!

第2部はこれで終了です。
長旅、お疲れ様でした!
ご清聴ありがとうございました。

【第1部のご紹介】
第1部は学習ポイントをギュッと集めた線形単回帰モデルの「概要」です。
ぜひお読みくださいね🍀
ブログの紹介
noteで3つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
2.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。
3.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、、Pythonのコラムを不定期に綴っています。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
