
「Pythonによる異常検知」を寄り道写経 ~ 第2章2.4節「高度な特徴抽出による異常検知」②EM法
第2章「非時系列データにおける異常検知」
書籍の著者 曽我部東馬 先生、監修 曽我部完 先生
この記事は、テキスト「Pythonによる異常検知」第2章「非時系列データにおける異常検知」2.4節「高度な特徴抽出による異常検知」の通称「寄り道写経」を取り扱います。
5回連続で高度な特徴抽出技術を利用した異常検知を寄り道写経します!
今回は EM法による異常検知です。
ではテキストを開いて異常検知の旅に出発です🚀

はじめに
テキスト「Pythonによる異常検知」のご紹介
このシリーズは書籍「Pythonによる異常検知」(オーム社、「テキスト」と呼びます)の寄り道写経です。
テキストは、2021年2月に発売され、機械学習等の誤差関数から異常検知を解明して、異常検知に関する実践的なPythonコードを提供する素晴らしい書籍です。
とにかく「誤差関数」と「異常度」の強い結びつきを堪能できる1冊です。
引用表記
この記事は、出典に記載の書籍に掲載された文章及びコードを引用し、適宜、掲載文章とコードを改変して書いています。
【出典】
「Pythonによる異常検知」第1版第6刷、著者 曽我部東馬、監修者 曽我部完、オーム社
記事中のイラストは、「かわいいフリー素材集いらすとや」さんのイラストをお借りしています。
ありがとうございます!
2.4 高度な特徴抽出による異常検知
主に Jupyter Notebook 形式(拡張子 .ipynb)でPythonコードを書きます。
今回の寄り道ポイントです。
EM法で異常検知を行います。
scikit-learn の GaussianMixture で EM法を実行します。
学習データで異常検知モデルを作成して、未知データの異常検知を行います。
学習データと未知データは前回と同じデータです。
手法間の違いを楽しみます!

この記事で用いるライブラリをインポートします。
### インポート
# 数値計算、確率計算
import numpy as np
import pandas as pd
### 機械学習
from sklearn.mixture import GaussianMixture
# 描画
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'
# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')
EM法(Expectation-maximization algorithm)
参考サイトの情報をお借りしてEMアルゴリズムを進めました。
ありがとうございます!
超要約すると「データが混合正規分布に従うと仮定して、EMアルゴリズムで混合正規分布を推定」します。
scikit-learn の GaussianMixture で算出される対数尤度(score_samplesで取得)を異常度にします。

準備
1.学習データの作成と可視化
前回の「k 平均法」と同じデータを使います。
2次元、300個の乱数データを作成します。
200個はグループ0、100個はグループ1を想定して、別々の2変量正規分布で乱数を作成します。
### データの作成
# 乱数生成器の設定
rng = np.random.default_rng(seed=1) # 23 or 24
# グループ0の200個のデータ作成:2変量正規分布乱数
group0 = rng.multivariate_normal(mean=[1, 1], cov=[[0.3, 0.081], [0.081, 0.3]],
size=200)
# グループ1の100個のデータ作成:2変量正規分布乱数
group1 = rng.multivariate_normal(mean=[-1, -1], cov=[[0.1, 0.009], [0.009, 0.1]],
size=100)
# データの統合
data = np.vstack([group0, group1])
print('data.shape:', data.shape)
print(data[:5, :], '…')
# グループラベルの作成
label_true = np.hstack([np.zeros(200), np.ones(100)]).astype(int)
print('\nグループラベル:', label_true[:10], '…')【実行結果】

学習データの散布図を描画して、分布などを確認しましょう。
### データの散布図の描画
# 描画領域の設定
fig, ax = plt.subplots(figsize=(6, 4))
# 散布図の描画
sns.scatterplot(x=data[:, 0], y=data[:, 1], hue=label_true, alpha=0.7,
palette=['tab:blue', 'tab:orange'], ax=ax)
# 凡例
handles, _ = ax.get_legend_handles_labels()
ax.legend(handles=handles, labels=['グループ0', 'グループ1'], title='正解ラベル')
# 修飾
ax.set(xlabel='変数1', ylabel='変数2', title='データの散布図')
ax.grid(lw=0.5);【実行結果】
2つのグループに分かれていますが、グループの境界あたりは少々入り乱れている感じもします。


異常検知モデルの構築
テキストの STEP に沿って、学習データによる異常検知モデルの構築に取り組みます。
1.STEP 1:EM法によるクラスタリングの実行
scikit-learn の GaussianMixture を使用して、学習データのクラスタリングを実行します。
クラスタ数は2です。
### STEP1 GaussianMixtureによるクラスタリングの実行
# クラスタ数の設定
n_components = 2
# GaussianMixtureの学習
gmm = GaussianMixture(n_components=n_components, random_state=1).fit(data)
# クラスタラベルの取得
cluster_label = gmm.predict(data)
print('cluster_label:', cluster_label[:10], '…')
# クラスタ中心点の取得
centers = gmm.means_【実行結果】
EM法のクラスタラベル(先頭10件)を表示しています。

あわせて、EM法のクラスタ中心点を centers に格納しています。
クラスタラベルでクラスタ識別した散布図を描画します。
### GaussianMixtureのクラスタラベルで層別した散布図の描画
## 等高線図用データの作成
# x,y軸の値の設定
x = y = np.linspace(-3, 4, 101)
X, Y = np.meshgrid(x, y)
# z軸:対数尤度xマイナスの算出
XX = np.array([X.ravel(), Y.ravel()]).T
Z = gmm.score_samples(XX) * -1
Z = Z.reshape(X.shape)
## 描画処理
# 描画領域の設定
fig, ax = plt.subplots(figsize=(6, 4))
# データ点の散布図の描画 クラスタリングラベルで色・形付け
sns.scatterplot(x=data[:, 0], y=data[:, 1], hue=cluster_label,
palette=['tab:blue', 'tab:orange'], alpha=0.7, ax=ax)
# 等高線図の描画
ax.contour(X, Y, Z, vmin=-5, vmax=8, levels=np.linspace(0, 15, 16),
cmap='Reds_r', linewidths=0.9)
# クラスタ中心点の描画
sns.scatterplot(x=centers[:, 0], y=centers[:, 1], marker='x', s=100, lw=3,
color='tab:red', ax=ax, legend=False)
# 凡例
handles, _ = ax.get_legend_handles_labels()
ax.legend(handles=handles, labels=['クラスタ0', 'クラスタ1'], title='gmm',
loc='upper left')
# 修飾
ax.set(xlabel='変数1', ylabel='変数2',
title='GaussianMixtureによるクラスタの散布図')
plt.grid(lw=0.5);【実行結果】
学習データのグループを完全に識別したクラスタリングができました。
2つのクラスタ中心点(×印)は程よい位置にあるような感じです。
等高線による中心点からの距離もいい感じですね!


2.STEP 2:クラスタごとの異常度の算出
混合正規分布(GaussianMixture)の対数尤度を異常度に見立てます。
score_samples の算出値は負値のため、$${-1}$$を掛けて正値に変換します。
### STEP2 異常度の算出 score_samplesの正負を反転する
anomaly_score = gmm.score_samples(data) * -1
print('anomaly_score.shape:', anomaly_score.shape)
print('anomaly_score[:5] :',anomaly_score[:5], '…')【実行結果】


3.STEP 3:異常度の閾値の算出
分位点法による閾値を算出します。
分位点は 1% です。
### STEP3 異常度の閾値の算出 by 分位点法
# 分位%点の設定
q = 0.01
# 閾値の算出
num_quantile = int(round(len(anomaly_score) * q, 0))
anomaly_thres = sorted(anomaly_score)[::-1][num_quantile - 1]
# 閾値の表示
print('分位点数:', num_quantile)
print('閾値:', anomaly_thres)【実行結果】

4.STEP 3-2:学習データで異常検知を確認
学習データの異常度に閾値を適用して異常検知を実行し、結果を可視化します。
### STEP3-2 学習データの異常検知
# 正常/異常ラベルの算出
anomaly_label = np.array((anomaly_score >= anomaly_thres) + 0)
# 算出結果の表示
print('anomaly_label.shape:', anomaly_label.shape)
print('anomaly_label[:10] :', anomaly_label[:10], '…')
print('異常データ数:', anomaly_label.sum())【実行結果】
学習データのうち、3点が異常判定となるモデルになりました。
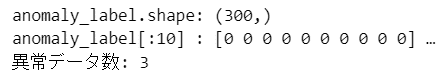
異常検知の結果を可視化します。
### STEP3-2 異常度と閾値を可視化して確認
## 異常度と閾値の可視化関数の定義
def plot_anomaly1(a_score, a_threshold, a_label, q):
# 設定
palette = ['tab:blue', 'tab:red']
sizes = [40, 80]
labels = ['正常', '異常']
# 正常データがない場合
if sum(a_label == 0) == 0:
palette = ['tab:red']
sizes = [80]
labels = ['異常']
# 描画領域の設定
fig, ax = plt.subplots(figsize=(6, 4))
# データの散布図の描画
sns.scatterplot(x=range(len(a_score)), y=a_score,
hue=a_label, palette=palette,
size=a_label, sizes=sizes)
# 閾値の水平線の描画
ax.axhline(a_threshold, color='tab:red', ls='--')
handles, _ = ax.get_legend_handles_labels()
ax.legend(handles=handles, labels=labels, bbox_to_anchor=(1, 1))
ax.set(xlabel='データ番号', ylabel='異常度 $\\alpha$',
title=f'EM法による異常度\n閾値 {a_threshold:.3f} (q={q:.0%})')
ax.grid(lw=0.5)
plt.show()
## 異常度の可視化
plot_anomaly1(anomaly_score, anomaly_thres, anomaly_label, q)
【実行結果】
いい感じに異常値を判別していると思います。


未知データの準備
未知データを作成して、さきほど構築した異常検知モデルに適用して異常検知しましょう!
1.未知データの作成
### 未知データの作成
data_new = np.array([[-1, 2], [-1, 0.3], [0, -1.5], [0, -1], [1, -1], [2, 0]])
print('未知データ:')
print(data_new)【実行結果】
6個のデータを作成しました。

未知データを可視化します。
### 未知データの可視化
# 描画領域の設定
fig, ax = plt.subplots(figsize=(6, 4))
# 学習データの散布図の描画
sns.scatterplot(x=data[:, 0], y=data[:, 1], hue=cluster_label,
palette=['tab:blue', 'tab:orange'], alpha=0.7, legend=False)
# kmeansのクラスタ中心点の描画
ax.scatter(centers[:, 0], centers[:, 1], marker='x', color='tab:red', s=200,
lw=3)
# 未知データの散布図の描画
ax.scatter(data_new[:, 0], data_new[:, 1], color='lightpink', ec='tab:red',
s=80, label='未知データ')
# 修飾
ax.set(xlabel='変数1', ylabel='変数2', title='未知データの散布図')
ax.legend()
ax.grid(lw=0.5);【実行結果】
クラスタの外側に配置しました。


未知データの異常検知
いよいよ本番です!
テキストの STEP に沿って、未知データの異常検知に取り組みます。
1.STEP 4:未知データのクラスタリング
学習済みの EM法クラスタリング器 gmm を用いて、未知データのクラスタリングを実行します。
### STEP4 未知データのクラスタの算出
cluster_label_new = gmm.predict(data_new)
print('未知データのクラスタ:', cluster_label_new)【実行結果】
3点がクラスタ 0(青い点側)、3点がクラスタ 1(オレンジ点側)になりました。

2.STEP 5 未知データの異常検知
判別されたクラスタの異常度計算・閾値を適用して異常データを炙り出します!
### STEP5 未知データの異常検知
## 未知データの異常度の算出
anomaly_score_new = gmm.score_samples(data_new) * -1
print('未知データの異常度 :', anomaly_score_new)
## 未知データの異常検知
anomaly_label_new = np.array((anomaly_score_new >= anomaly_thres) + 0)
print('未知データの異常検知:', anomaly_label_new)【実行結果】
未知データの1番目、2番目、3番目、5番目が異常判定されました!
異常値だらけ!?

未知データの異常検知結果をデータフレーム化しましょう。
### 未知データの異常検知結果のデータフレームの作成
data_new_df = pd.DataFrame(data_new, columns=['変数1', '変数2'])
data_new_df['クラスタ'] = cluster_label_new
data_new_df['異常度'] = anomaly_score_new
data_new_df['閾値'] = anomaly_thres
data_new_df['異常検知'] = anomaly_label_new
display(data_new_df)【実行結果】


3.異常検知結果を可視化
未知データの異常検知結果をさまざまな可視化手法で堪能しましょう。
① 異常度の散布図
### 異常度の可視化
plot_anomaly1(anomaly_score_new, anomaly_thres, anomaly_label_new, q)【実行結果】
未知データの異常度はさまざまな値をとっていることが分かります。

② 2変数の散布図に正常・異常をマップ
学習データを含む2変数の散布図に未知データを追加してみましょう。
未知データは正常・異常を識別してプロットします。
### 未知データのクラスタ&異常検知の可視化
# 描画領域の設定
fig, ax = plt.subplots(figsize=(6, 4))
# 学習データの散布図の描画
sns.scatterplot(x=data[:, 0], y=data[:, 1], hue=cluster_label,
palette=['tab:blue', 'tab:orange'], alpha=0.5, legend=False,
ax=ax)
# クラスタ中心点の描画
ax.scatter(centers[:, 0], centers[:, 1], marker='x', color='tab:red', s=200,
lw=3)
# 未知データの散布図の描画
sns.scatterplot(x=data_new[:, 0], y=data_new[:, 1],
hue=cluster_label_new, palette=['tab:blue', 'tab:orange'],
alpha=0.7, ec='tab:red',
style=anomaly_label_new, markers=['o', 'X'],
size=anomaly_label_new, sizes=[200, 250], legend=False,
ax=ax)
for i in range(len(data_new)):
ax.annotate(text=i, xy=data_new[i, :]+0.12, fontsize=14)
# 凡例
ax.scatter([], [], marker='o', c='tab:blue', alpha=0.7, s=70, label='クラスタ0')
ax.scatter([], [], marker='o', c='tab:orange', alpha=0.7, s=70, label='クラスタ1')
ax.scatter([], [], marker='o', c='white', ec='tab:red', s=70, label='正常')
ax.scatter([], [], marker='X', c='white', ec='tab:red', s=100, label='異常')
ax.legend(bbox_to_anchor=(1, 1))
# 修飾
ax.set(xlabel='変数1', ylabel='変数2', title='未知データの異常検知')
ax.grid(lw=0.5);【実行結果】
青色がクラスタ 0、オレンジ色がクラスタ 1 です。
形状が◯印のデータは正常、X印のデータは異常です。

クラスタ1のデータ点1と3に注目します。
データ点1の方が中心点×に近いのですが、異常値と判定されました。
一方でデータ点3は正常値です。
正規分布の形状、特に分散の影響がありそうです。
クラスタ0と1を判別する決定境界を追加描画しましょう。
③ 決定境界付き散布図
scikit-learn の DecisionBoundaryDisplay を使えば簡単に決定境界を描画できます!
### 決定境界の描画
# 追加インポート
from sklearn.inspection import DecisionBoundaryDisplay
from matplotlib.colors import ListedColormap
# 色の設定
cmap_bound = ListedColormap(['lightblue', 'bisque'])
# 描画領域の設定
fig, ax = plt.subplots(figsize=(6, 4))
# 決定境界の描画
disp = DecisionBoundaryDisplay.from_estimator(
gmm, data, response_method='predict', cmap=cmap_bound,
xlabel='Magnesium', ylabel='Color intensity', alpha=0.3, ax=ax)
# 学習データの散布図の描画
sns.scatterplot(x=data[:, 0], y=data[:, 1], hue=cluster_label,
palette=['tab:blue', 'tab:orange'], alpha=0.5, legend=False,
ax=ax)
# kmeansのクラスタ中心点の描画
ax.scatter(centers[:, 0], centers[:, 1], marker='x', color='tab:red', s=200,
lw=3)
# 未知データの散布図の描画
sns.scatterplot(x=data_new[:, 0], y=data_new[:, 1],
hue=cluster_label_new, palette=['tab:blue', 'tab:orange'],
alpha=0.7, ec='tab:red',
style=anomaly_label_new, markers=['o', 'X'],
size=anomaly_label_new, sizes=[200, 250], legend=False,
ax=ax)
# 凡例表示
ax.scatter([], [], marker='o', c='tab:blue', alpha=0.7, s=70, label='クラスタ0')
ax.scatter([], [], marker='o', c='tab:orange', alpha=0.7, s=70, label='クラスタ1')
ax.scatter([], [], marker='o', c='white', ec='tab:red', s=70, label='正常')
ax.scatter([], [], marker='X', c='white', ec='tab:red', s=100, label='異常')
ax.legend(bbox_to_anchor=(1.3, 1))
# 修飾
ax.set(xlabel='変数1', ylabel='変数2', title='未知データの異常検知と決定境界')
ax.grid(lw=0.5);【実行結果】
クラスタを判別する「決定境界」が明らかになりました!
曲線の境界になっています。
クラスタ0の勢力が大きいですね!

この図はあくまでクラスタ判別基準だけを示しています。
正常・異常の境界はどうなっているのでしょう???
描いてみましょう!!!
④ 決定境界付き閾値付き散布図
地道に等高線を描画します!
### 閾値の描画
## 描画処理
# 描画領域の設定
fig, ax = plt.subplots(figsize=(6, 4))
# 決定境界の描画
disp = DecisionBoundaryDisplay.from_estimator(
gmm, data, response_method='predict', cmap=cmap_bound,
xlabel='変数1', ylabel='変数2', alpha=0.3, ax=ax)
# 学習データの散布図の描画
sns.scatterplot(x=data[:, 0], y=data[:, 1], hue=cluster_label,
palette=['tab:blue', 'tab:orange'], alpha=0.5, legend=False,
ax=ax)
# 未知データの散布図の描画
sns.scatterplot(x=data_new[:, 0], y=data_new[:, 1],
hue=cluster_label_new, palette=['tab:blue', 'tab:orange'],
alpha=0.7, ec='tab:red',
style=anomaly_label_new, markers=['o', 'X'],
size=anomaly_label_new, sizes=[200, 250], legend=False,
ax=ax)
# クラスタ中心点の描画
ax.scatter(centers[:, 0], centers[:, 1], marker='x', color='tab:red', s=200,
lw=3)
# 等高線図の描画
ax.contour(X, Y, Z, vmin=-5, vmax=8, levels=np.linspace(0, 15, 16),
cmap='Reds_r', linewidths=0.9)
# 閾値の描画
ax.contour(X, Y, Z, vmin=-5, vmax=8, levels=[anomaly_thres],
colors=['tab:red'], linestyles=['--'])
# 凡例表示
ax.scatter([], [], marker='o', c='tab:blue', alpha=0.7, s=70, label='クラスタ0')
ax.scatter([], [], marker='o', c='tab:orange', alpha=0.7, s=70, label='クラスタ1')
ax.scatter([], [], marker='o', c='white', ec='tab:red', s=70, label='正常')
ax.scatter([], [], marker='X', c='white', ec='tab:red', s=100, label='異常')
ax.plot([], [], c='tab:red', ls='--', label='閾値')
ax.legend(bbox_to_anchor=(1.3, 1))
# 修飾
ax.set(title='未知データの異常検知\nクラスタの決定境界と異常値の閾値',
xlim=(-2.7, 3.5), ylim=(-2.7, 4.1))
ax.grid(lw=0.5);【実行結果】
等高線図に赤い点線の異常度の閾値をプロットしました。
今回の EM法による2次元データの異常検知マップ(地図)が明確になりました。
k 平均法と比べると、データ点4のクラスタ判別が異なり、データ点2の異常判定が異なっています。

(参考:k 平均法の決定境界と閾値)

今回の寄り道写経は以上です。
シリーズの記事
次の記事
前の記事
目次
ブログの紹介
note で7つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
Python、EXCELのサンプルコードの配布もあります。
2.実験!たのしいベイズモデリング1&2をPyMC Ver.5で
書籍「たのしいベイズモデリング」・「たのしいベイズモデリング2」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは R言語+Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう!
3.実験!岩波データサイエンス1のベイズモデリングをPyMC Ver.5で
書籍「実験!岩波データサイエンスvol.1」の4人のベイジアンによるベイズモデルを PyMC Ver.5で描いて分析します。
この書籍はベイズプログラミングのイロハをざっくりと学ぶことができる良書です。
楽しくPyMCモデルを動かして、ベイズと仲良しになれた気がします。
みなさんもぜひぜひPyMCで動かして、一緒に遊んで学びましょう!
4.楽しい写経 ベイズ・Python等
ベイズ、Python、その他の「書籍の写経活動」の成果をブログにします。
主にPythonへの翻訳に取り組んでいます。
写経に取り組むお仲間さんのサンプルコードになれば幸いです🍀
5.RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析をPythonとPyMC Ver.5 で実践します。
この書籍には時系列分析のテーマが盛りだくさん!
時系列分析の懐の深さを実感いたしました。
大好きなPythonで楽しく時系列分析を学びます。
6.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
統計・データサイエンス書籍にまつわる記事が多いです。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
7.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。
最後までお読みいただきまして、ありがとうございました。
