9-2-3 期待度数・独立性検定～２つの薬に効果の違いがあるかどうかを独立性の検定で確かめる

ネイピア DS

2023年10月11日 12:01

統計的仮説検定のトピック「独立性の検定」の第３回です。
目を瞑って$${\chi^2}$$の検定の手続きができるようになりましたか！？
まだまだ続きますよっ！

公式問題集の準備

「公式問題集」の問題を利用します。お手元に公式問題集をご用意ください。
公式問題集が無い場合もご安心ください！
「知る」「実践する」の章で、のんびり統計をお楽しみください！

問題を解いて、知る・実践する

今回の記事の構成

この記事は、通常の記事構成と違う章立てにいたします。
「問題を解く」「知る」「実践する」を１つの章にまとめます。
独立性の検定の一連の流れを、手作業・EXCEL・Pythonで実践いたします。

📘公式問題集のカテゴリ

カイ二乗検定の分野　～独立性検定の分野
問3 期待度数・独立性検定（２種類の薬剤の効果）

試験実施年月
調査中

📕公式テキスト：6.3 独立性の検定（205ページ～）

問題

公式問題集をご参照ください。

解き方

題意
与えられた条件を紐解き、期待度数の一部を明らかにして、独立性の検定の結果（結論）を解答します。

【条件】
・「薬剤」２行・「効果」２列の２元クロス集計表に基づいて独立性の検定を行う
・有意水準は$${5\%}$$
・帰無仮説は「２種類の薬の効果には差がない」（独立である）
・観測度数は次の表のとおり

公式問題集の記述を改変

読み解き

条件から統計的仮説検定の主題を読み解きます。

条件より、有意水準$${5\%}$$「独立性の検定」を行います。
独立性の検定は「片側検定（上側）」です。
クロス集計表の２つの「変数は独立である」との帰無仮説の下で、期待度数を計算します。
観測度数と期待度数を用いて、検定統計量$${\chi^2}$$を計算します。
検定統計量$${\chi^2}$$が従う$${\chi^2}$$分布の自由度を計算します。
$${\chi^2}$$分布のパーセント点表より、有意水準$${5\%}$$のパーセント点を取得して、帰無仮説を棄却できるかどうか結論づけます。

この問題の統計的仮説検定の概要を図示します。

統計的仮説検定の手段

今回は、①手計算、②EXCEL、③Python の３つの手段で検定を実施いたします。

手計算で検定

ステップ１：期待度数を計算する

期待度数は、帰無仮説が正しいと仮定してカウントする度数です。

全ての観測度数を計算する前に、出題の「薬剤A・改善した」の観測度数を計算しましょう。

観測度数を確認します。

「改善」縦計は９０、「薬剤A」横計は６４、合計は１２０。
クロスする縦計と横計を掛けて合計で割ると期待度数が求まります。

「薬剤A・改善」の期待度数は$${48}$$です。

次のように考えることもできます。

解答選択肢（ア）の期待度数は A2 : 48 です。

期待度数の全体像に戻ります。

独立性の検定の場合、クロス集計表の２変数は独立である、と仮定して期待度数を計算します。

帰無仮説を独立な２つの事象の確率の数式を用いて表します。

帰無仮説 $${H_0 : P(A_i \cap B_j)=P(A_i)P(B_j)}$$

ただし、$${i,j}$$：クロス集計表の行と列、$${A_i}$$：薬剤のカテゴリ、$${B_i}$$：効果のカテゴリ、$${P(A_i \cap B_j)}$$：薬剤と効果の積事象の確率（同時確率）、$${P(A_i), P(B_i)}$$：薬剤の確率と効果の確率（周辺確率）

この数式をクロス集計表にマッピングしてみます。
期待度数の確率が見えてきました。

横計$${P(A_i)}$$と縦計$${P(B_i)}$$を計算しましょう。
これらの比率は周辺確率と呼ばれるものです。

$$
P(A_1)=64/120=0.533 \\
P(A_2)=56/120=0.467 \\
P(B_1)=90/120=0.750 \\
P(B_2)=30/120=0.250 \\
$$

計算結果を表にします。

期待度数の確率は、縦計の比率（周辺確率）と横計の比率（周辺確率）を掛け算した値です。
期待度数の確率を計算しましょう。

期待度数の確率と標本サイズ（合計）$${120}$$を掛け算して、期待度数を算出します。

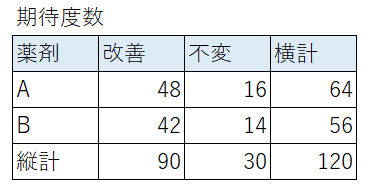
【時短計算法】
次の表のように観測度数の「縦計」「横計」「総合計」から期待度数を計算できます。

次の計算で観測度数と期待度数を用いるので、両方の度数をまとめて掲載しましょう。

棒グラフで観測度数と期待度数の違いを可視化しましょう。

観測度数には、薬剤Aの方が改善の割合が大きくて、Bの方が変わらなかったの割合が大きい「効果の偏りのようなもの」が見られます。
はたして、独立性の検定の結果はいかに・・・。

ステップ２：検定統計量$${\boldsymbol{\chi^2}}$$を計算する

カテゴリ（分類）ごとに「観測度数と期待度数の差の２乗」を「期待度数で割り」、全カテゴリを合計します。

本問のカテゴリは行２×列２で合計４のカテゴリがあります。
・行：「A」と「B」の２つ
・列：「改善した」と「変わらなかった」の２つ

検定統計量$${\chi^2}$$は次の計算式を用いて計算します。

先程まとめた観測度数と期待度数の値を当てはめて、検定統計量$${\chi^2}$$を計算しましょう。

検定統計量の計算で得られた$${\chi^2}$$値は$${4.46}$$です。

【時短計算法】
２×２クロス集計表から期待度数を計算する場合、各カテゴリの分子の値は同じになります。
上の計算式の２行目をご確認ください。

また、分子の値は次の計算式で求めることができます。
$${ \left(\cfrac{ad-bc}{a+b+c+d} \right)^2}$$
計算式中の$${a,b,c,d}$$は下の観測度数のクロス集計表を参照してください。

ステップ３：検定統計量$${\boldsymbol{\chi^2}}$$が従う$${\boldsymbol{\chi^2}}$$分布の自由度

２元クロス集計表を用いて、独立性の検定を行う場合、自由度の計算式は次のようになります。

■自由度の公式
（行のカテゴリの数－１）×（列のカテゴリの数－１）
もしくは
$${(r-1)(c-1)}$$
ただし、$${r}$$：行のカテゴリの数、$${c}$$：列のカテゴリの数

本問で取り扱う観測度数のカテゴリ数は「行$${r}$$：A・Bの２つ」「列$${c}$$：改善した・変わらなかったの２つ」です。
自由度は、$${(r-1)(c-1)=(2-1)\times(2-1)=1\times1=1}$$で、$${1}$$です。

解答選択肢（イ）の一部である自由度は$${1}$$です。

ステップ４：検定統計量$${\boldsymbol{\chi^2}}$$が従う$${\boldsymbol{\chi^2}}$$分布の上側パーセント点

続いて上側パーセント点を取得して棄却域を確認します。
ここで重要なお知らせ。

【重要ポイント】
・独立性の検定は片側・上側検定です。

独立性の検定は片側・上側検定ですので、有意水準$${5\%}$$の棄却域を求める際には、自由度$${1}$$の$${\chi^2}$$分布のパーセント点表より上側確率$${5\%}$$点を取得します。

自由度$${1}$$の上側確率$${5\%}$$点は$${3.84}$$です。

$${\chi^2}$$分布の確率密度関数をグラフで確認しましょう。

垂直の滑り台のような形状です（２回目）。

ステップ５：結論を出す

$${\chi^2}$$値$${=4.46}$$と上側確率$${5\%}$$点$${=3.84}$$を比べます。
$${\chi^2}$$値は上側確率$${5\%}$$点より大きいため、棄却域の区間内です。
よって、帰無仮説は棄却されます。

具体的には、有意水準$${5\%}$$で帰無仮説「２種類の薬の効果には差がない」（独立である）は棄却され、対立仮説「２種類の薬の効果に差がある」（独立ではない）と言えます。

解答選択肢（イ）は B1 : 「検定統計量の値は、自由度１のカイ二乗分布の上側$${5\%}$$点より大きいので、『２種類の薬の効果に差がある』」です。

最後にグラフで棄却域と$${\chi^2}$$値の関係を確認しましょう。

確かに$${\chi^2}$$値は棄却域に含まれています。

手計算は以上となります。

EXCELで検定

計算シートを用いて独立性の検定を行います。

計算シートの全体像
左側の表には、観測度数と仮定する分布（確率）を登録します。

観測度数に基づいて期待度数を計算しています。
また、カテゴリごとに$${(観測度数-期待度数)^2/期待度数}$$の計算を行って合計を取り、$${\chi^2}$$値にしています。
右側の入力パラメータは「有意水準」です。

観測度数・期待度数・有意水準より、$${\chi^2}$$値、上側確率％点、$${p}$$値を求めて、判定します。

独立性の検定の実行

上記の計算シートには既に必要なデータ、パラメータを設定済みです。
計算値によると、自由度は$${1}$$、$${\chi^2}$$値は$${4.464}$$、上側確率$${5\%}$$点は$${3.841}$$です。
$${\chi^2}$$値が上側確率$${5\%}$$点よりも大きいので、帰無仮説は棄却されます。
$${p}$$値は$${0.035}$$でした。

まとめ

$${\chi^2}$$値は$${4.464}$$、$${p}$$値は$${0.035}$$です。
有意水準$${5\%}$$で帰無仮説は棄却され、対立仮説「２種類の薬の効果に差がある」（独立ではない）と言えます。

EXCELの関数

EXCELの CHISQ.TEST 関数を用いて、独立性の検定の$${p}$$値を算出できます。
引数は、CHISQ.TEST ( 観測度数のデータ範囲, 期待度数のデータ範囲 ) です。
２元クロス集計表の場合も、観測度数の期待度数の行と列を揃えておくことで、データ範囲の指定を容易に行なえます。
シンプルなのでぜひ使ってみてください！

EXCELは以上となります。

EXCELサンプルファイルのダウンロード
こちらのリンクからEXCELサンプルファイルをダウンロードできます。

Pythonで検定

scipy.stats の chi2_contingency を用いて、クロス集計表に基づく独立性の検定を実行します。

①インポート

### インポート
import numpy as np
import pandas as pd
from scipy import stats
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'Meiryo'

②データとパラメータの設定
問題で与えられたクロス集計表（観測度数）を登録して、pandasのデータフレーム observed_tab を作成します。

### データとパラメータの設定

## データ、パラメータの登録
# 観測度数　行：薬剤、列：効果
observed_array = np.array([[53, 11], [37, 19]])
# 有意水準
alpha = 0.05

## データフレーム化
observed_tab = pd.DataFrame(observed_array,
                            columns=['改善した', '変わらなかった'],
                            index=['A', 'B'])
observed_tab

③独立性の検定の実施
scipy.stats の chi2_contingency を用いて独立性の検定を行います。
最初の１行だけで独立性の検定を処理できています。

引数は、chi2_contingency ( 観測データのクロス集計表, correction ) です。
期待度数を用意する必要が無いので、とても手軽に検定を実行できます。
correction=False はイエーツの補正を実施しない、というオマジナイです。
戻り値は、$${\chi^2}$$値、$${p}$$値、自由度、期待度数です。

### 独立性の検定の実施　クロス集計表をインプット
chi2_value, p_value, df, expected = stats.chi2_contingency(observed_tab,
                                                           correction=False)

# 期待度数のデータフレーム化
expected_tab = pd.DataFrame(expected, columns=observed_tab.columns,
                              index=observed_tab.index)
# 期待度数の表示
print('期待度数:')
display(expected_tab)

# カイ二乗統計量、p値、自由度の表示
print(f'χ^2値:{chi2_value:.3f}, p値:{p_value:.3f}, 自由度:{df}')

④結論の表示
有意水準と$${p}$$値を比較して、帰無仮説を棄却できるかどうかを判定します。

### 結論の表示

# 有意水準のカイ二乗分布の上側パーセント点の取得
critical_value = stats.chi2.isf(alpha, df)

if p_value < alpha:  # p値が有意水準より小さい場合：棄却できる
    result = ('棄却される', '言える')
else:                # p値が有意水準以上の場合：棄却できない
    result = ('棄却されない', '言えない')
print(f'結論\n有意水準{alpha:.1%}で帰無仮説は{result[0]}\n'
      f'対立仮説「各変数は独立でない（関連がある）」と{result[1]}')

### 統計量の表示
print('\n統計量')
print(f'自由度{df}のカイ二乗分布の上側{alpha:.1%}点:{critical_value:.3f}, '
      f'カイ二乗値:{chi2_value:.3f}')
print(f'有意水準{alpha:.3f}, p値:{p_value:.3f}')

帰無仮説を棄却できました。

まとめ
観測度数のクロス集計表データを整えて、scipy.stats の chi2_contingency を実行するだけで、$${p}$$値を取得して独立性の検定の結論を出せることが分かりました。

$${p}$$値が有意水準$${5\%}$$より小さいので、有意水準$${5\%}$$で帰無仮説は棄却され、対立仮説「２種類の薬の効果に差がある」（独立ではない）と言えます。

Pythonサンプルファイルのダウンロード
こちらのリンクからJupyter Notebook形式のサンプルファイルをダウンロードできます。

以上で終了です。
お疲れ様でした。

解答

② です。

難易度　やさしい

・知識：独立性の検定、$${\chi^2}$$分布のパーセント点表
・計算力：数式組み立て（低）、電卓（中）
・時間目安：2分

おわりに

朝晩の冷え込みが身体に堪える季節になりました。
少し前までの暑さがまるで嘘のようです。
季節の変わり目です。どうぞご自愛下さいませ。

ところで独立性の検定の第３回目、いかがだったでしょう。
期待度数の計算に慣れたでしょうか？
次回は独立性の検定の最終回です。

最後までお読みいただきまして、ありがとうございました。

のんびり統計シリーズの記事

次の記事

前の記事

この記事が気に入ったらサポートをしてみませんか？