
「数値シミュレーションで読み解く統計のしくみ」をPythonで写経 ~ 第4章4.1「統計的推測の基礎」
第4章「母数の推定のシミュレーション」
書籍の著者 小杉考司 先生、紀ノ定保礼 先生、清水裕士 先生
この記事は、テキスト「数値シミュレーションで読み解く統計のしくみ」第4章「母数の推定のシミュレーション」4.1節「統計的推測の基礎」の Python写経活動 を取り扱います。
今回はシミュレーションを通じて母数の推定量が持つ性質「一致性」「不偏性」「有効性」を確認します。
R の基本的なプログラム記法はざっくり Python の記法と近いです。
コードの文字の細部をなぞって、R と Python の両方に接近してみましょう!
ではテキストを開いてシミュレーションの旅に出発です🚀

はじめに
テキスト「数値シミュレーションで読み解く統計のしくみ」のご紹介
このシリーズは書籍「数値シミュレーションで読み解く統計のしくみ〜Rでためしてわかる心理統計」(技術評論社、「テキスト」と呼びます)の Python写経です。
テキストは、2023年9月に発売され、副題「Rでためしてわかる心理統計」のとおり、統計処理に定評のある R の具体的なコードを用いて、心理統計の理解に役立つ数値シミュレーションを実践する素晴らしい書籍です。
引用表記
この記事は、出典に記載の書籍に掲載された文章及びコードを引用し、適宜、掲載文章とコードを改変して書いています。
【出典】
「数値シミュレーションで読み解く統計のしくみ〜Rでためしてわかる心理統計」初版第1刷、著者 小杉考司・紀ノ定保礼・清水裕士、技術評論社
記事中のイラストは、「かわいいフリー素材集いらすとや」さんのイラストをお借りしています。
ありがとうございます!
4.1 統計的推測の基礎
母集団の特徴を表す値を母数(パラメータ)と呼び、母集団の平均・分散は母数の一例です。
母集団からサンプリングした標本を用いて母数を統計的に推定します。
母数を推定するための標本統計量を推定量と呼びます。
テキストは推定量の望ましい性質「一致性」「不偏性」「有効性」をシミュレーションを利用して、説明します。
この記事は Jupyter Notebook 形式(拡張子 .ipynb)でPythonコードを書きます。
概ね確率分布の特性値算出には scipy.stats を用い、乱数生成には numpy.random.generator を用いるようにしています。
主に利用するライブラリをインポートします。
### インポート
# 数値計算
import numpy as np
# 確率・統計
import scipy.stats as stats
# 描画
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'Meiryo'
4.1.3 一致性
サンプルサイズが大きくなるほど母数に近づく推定量の性質を一致性と呼び、一致性を持つ推定量を一致推定量と呼びます。
「サンプルサイズが大きくなるほど母数に近づく」ことをサンプルサイズをどんどん大きくするシミュレーションで確認します。
■ シミュレーションの「サンプルサイズ」データを作成
10から20000までを10間隔で区切った数値群をサンプルサイズにします。
### 122ページ サンプルサイズを表す数列を生成
# サンプルサイズ
s_size = np.arange(10, 20000 + 1, 10)
# 冒頭の要素3つ、末尾の要素3つを表示
print(s_size)【実行結果】

シミュレーションするサンプルサイズの数をカウントします。
### 122ページ s_sizeの長さ
len(s_size)【実行結果】
サンプルサイズの数が 2000、ということは、シミュレーションを2000回行います!


母平均の一致推定量
■ 標本平均が母平均の一致推定量であることをシミュレーション
テキストによると「平均$${\mu}$$の母集団分布に互いに独立に従う確率変数の標本平均は母平均$${\mu}$$の一致推定量」です。
サンプルサイズがどんどん大きくなると標本平均が母平均に近づくことをシミュレーションします。
平均パラメータ0、標準偏差1の正規分布乱数を生成します。
母平均は0です。
### 122ページ 標本平均を作成して一致性を可視化 123ページ図4.1
# 2000個の標本平均を格納するオブジェクト
sample_mean = np.zeros(len(s_size))
## シミュレーション
rng = np.random.default_rng(seed=1)
for i in range(len(s_size)):
sample_mean[i] = rng.normal(size=s_size[i], loc=0, scale=1).mean()
## 結果
# 折れ線グラフの描画
plt.plot(s_size, sample_mean, color='tab:blue', alpha=0.5)
# y = 0の位置に、白い水平線を描画
plt.axhline(0, color='white', linewidth=2)
# x軸ラベル・y軸ラベルの設定
plt.xlabel('sample size')
plt.ylabel('sample mean');【実行結果】
横軸はサンプルサイズ、縦軸は標本平均です。
サンプルサイズが大きくなるにつれて、標本平均は母平均の0に近づく様子が分かりました!

【コード補足】
確率分布の乱数生成には numpy の random generator を使用しています。
rng = np.random.default_rng(seed=1)
この部分で乱数生成器 rng を作成しています。
乱数シードも設定しています。
rng.normal(size=s_size[i], loc=0, scale=1)
この部分で正規分布乱数を生成しています。
パラメータは次の通り。
size:生成する乱数の数
loc:正規分布の場合、平均
scale:正規分布の場合、標準偏差
■ 幾何平均が母平均の一致推定量ではないことをシミュレーション
標本の幾何平均は母平均の一致推定量ではありません。
サンプルサイズがどんどん大きくなっても標本の幾何平均が母平均に近づかないことをシミュレーションします。
平均パラメータ 100、標準偏差 10 の正規分布乱数を生成します。
母平均は 100 です。
### 123ページ 幾何平均の算出と可視化 124ページ図4.2
## 設定と準備
# 幾何平均を返す関数を定義
def g_mean(x):
return np.exp(np.log(x).mean())
# 母平均
mu = 100
# 母標準偏差
sigma = 10
# 結果を格納するオブジェクト
sample_mean = np.zeros(len(s_size))
## シミュレーション
rng = np.random.default_rng(seed=1)
for i in range(len(s_size)):
sample_mean[i] = g_mean(rng.normal(size=s_size[i], loc=mu, scale=sigma))
## 結果
# 折れ線グラフの描画
plt.plot(s_size, sample_mean, color='tab:blue', alpha=0.5)
# y = μの位置に、赤い水平線を描画
plt.axhline(mu, color='tomato', linewidth=2)
# x軸ラベル・y軸ラベルの設定
plt.xlabel('sample size')
plt.ylabel('sample mean');【実行結果】
サンプルサイズが大きくなるにつれて 99.5 あたりに収斂しています。
母平均 100 にはなりませんでした。

■ ちなみに情報:scipy の gmean 関数
scipy に 幾何平均を算出できる関数 gmean がありますので、試してみましょう。
あわせて、for 文でシミュレーションする箇所をリスト内包表記に変えて、コードをシンプルにしてみます、
### 123ページ 幾何平均の算出と可視化 別解 scipyのgmean関数、リスト内包表記
## 設定と準備
# 母平均
mu = 100
# 母標準偏差
sigma = 10
## シミュレーション
rng = np.random.default_rng(seed=1)
sample_mean = [stats.gmean(rng.normal(size=s, loc=mu, scale=sigma))
for s in s_size]
## 結果
# 折れ線グラフの描画
plt.plot(s_size, sample_mean, color='tab:blue', alpha=0.5)
# y = μの位置に、赤い水平線を描画
plt.axhline(mu, color='tomato', linewidth=2)
# x軸ラベル・y軸ラベルの設定
plt.xlabel('sample size')
plt.ylabel('sample mean');【実行結果】
上のグラフとほぼ同じ結果を得られました。

■ 母集団分布にt分布を仮定して標本平均をシミュレーション
母集団分布にt分布を仮定した場合にも標本平均が母平均の一致推定量であることをシミュレーションで確かめます。
自由度4のt分布です。
### 124ページ 自由度4のt分布の標本平均、一致性を可視化 125ページ図4.3
## 設定と準備
# t分布の自由度パラメータ
nu = 4
## シミュレーション
rng = np.random.default_rng(seed=3)
sample_mean = [rng.standard_t(size=s, df=nu).mean() for s in s_size]
## 結果
# 折れ線グラフの描画
plt.plot(s_size, sample_mean, color='tab:blue', alpha=0.5)
# y = 0の位置に、白い水平線を描画
plt.axhline(0, color='white', linewidth=2)
# x軸ラベル・y軸ラベルの設定
plt.xlabel('sample size')
plt.ylabel('sample mean');【実行結果】
母集団分布にt分布を仮定しても、標本平均の一致性を確認できました。

■ 母集団分布に標準コーシー分布を仮定して標本平均をシミュレーション
母集団が標準コーシー分布の場合、標本平均は母平均の一致推定量にはならないそうです。
シミュレーションで確かめます。
標準コーシー分布は自由度1のt分布に一致するそうです。
### 125ページ 自由度1のt分布=標準コーシー分布の標本平均、可視化 126ページ図4.4
## 設定と準備
# t分布の自由度パラメータ
nu = 1
## シミュレーション
rng = np.random.default_rng(seed=3)
sample_mean = [rng.standard_t(size=s, df=nu).mean() for s in s_size]
## 結果
# 折れ線グラフの描画
plt.plot(s_size, sample_mean, color='tab:blue', alpha=0.5)
# y = 0の位置に、赤いい水平線を描画
plt.axhline(0, color='tomato', linewidth=2)
# x軸ラベル・y軸ラベルの設定
plt.xlabel('sample size')
plt.ylabel('sample mean');【実行結果】
標本平均がときどき大きく暴れています。
たしかに母集団分布が標準コーシー分布の場合、標本平均は一致性を持たないようです。


母分散の一致推定量
■ 不偏分散が母分散の一致推定量であることをシミュレーション
テキストによると「平均$${\mu}$$、分散$${\sigma^2}$$の母集団分布に互いに独立に従う確率変数の標本分散や不偏分散は母分散$${\sigma^2}$$の一致推定量」です。
不偏分散を確かめます。
サンプルサイズがどんどん大きくなると不偏分散が母分散に近づくことをシミュレーションします。
自由度4のt分布乱数を生成します。
母分散は2です。
### 126ページ 自由度4のt分布の不偏分散、一致性を可視化 127ページ図4.5
## 設定と準備
# t分布の自由度パラメータ
nu = 4
## シミュレーション ※ var(ddof=1)は不偏分散を返す
rng = np.random.default_rng(seed=1)
sample_var = [rng.standard_t(size=s, df=nu).var(ddof=1) for s in s_size]
## 結果
# 折れ線グラフの描画
plt.plot(s_size, sample_var, color='tab:blue', alpha=0.5)
# y = σ²の位置に、白い水平線を描画
plt.axhline(nu / (nu - 2), color='white', linewidth=2)
# x軸ラベル・y軸ラベルの設定
plt.xlabel('sample size')
plt.ylabel('unbiased variance');【実行結果】
ときどき暴れていますが、サンプルサイズが大きくなるにつれて、不偏分散は母分散の2に近づく様子が分かりました!

■ 標本分散が母分散の一致推定量であることをシミュレーション
続いて標本分散の確認です。
サンプルサイズがどんどん大きくなると標本分散が母分散に近づくことをシミュレーションします。
自由度4のt分布乱数を生成します。
母分散は2です。
### 自由度4のt分布の標本分散、一致性を可視化
## 設定と準備
# t分布の自由度パラメータ
nu = 4
## シミュレーション ※var(ddof=0)は標本分散を返す
rng = np.random.default_rng(seed=1)
sample_var = [rng.standard_t(size=s, df=nu).var(ddof=0) for s in s_size]
## 結果
# 折れ線グラフの描画
plt.plot(s_size, sample_var, color='tab:blue', alpha=0.5)
# y = σ²の位置に、白い水平線を描画
plt.axhline(nu / (nu - 2), color='white', linewidth=2)
# x軸ラベル・y軸ラベルの設定
plt.xlabel('sample size')
plt.ylabel('unbiased variance');【実行結果】
ときどき暴れていますが、サンプルサイズが大きくなるにつれて、標本分散は母分散の2に近づく様子が分かりました!

■ 母集団分布に標準コーシー分布を仮定して不偏分散・標本分散をシミュレーション
母集団が標準コーシー分布の場合、不偏分散・標本分散は母分散の一致推定量にはならないそうです。
シミュレーションで確かめます。
まずは不偏分散から。
### 自由度1のt分布=標準コーシー分布の不偏分散 可視化
## 設定と準備
# t分布の自由度パラメータ
nu = 1
## シミュレーション ※var(ddof=1)は不偏分散を返す
rng = np.random.default_rng(seed=1)
sample_var = [rng.standard_t(size=s, df=nu).var(ddof=1) for s in s_size]
## 結果
# 折れ線グラフの描画
plt.plot(s_size, sample_var, color='tab:blue', alpha=0.5)
# y = σ²の位置に、赤い水平線を描画
plt.axhline(nu / (nu - 2), color='tomato', linewidth=2)
# x軸ラベル・y軸ラベルの設定
plt.xlabel('sample size')
plt.ylabel('unbiased variance');【実行結果】

続いて標本分散です。
### 自由度1のt分布=標準コーシー分布の標本分散 可視化
## 設定と準備
# t分布の自由度パラメータ
nu = 1
# 結果を格納するオブジェクト
sample_var = np.zeros(len(s_size))
## シミュレーション ※var(ddof=0)は標本分散を返す
rng = np.random.default_rng(seed=1)
sample_var = [rng.standard_t(size=s, df=nu).var(ddof=0) for s in s_size]
## 結果
# 折れ線グラフの描画
plt.plot(s_size, sample_var, color='tab:blue', alpha=0.5)
# y = σ²の位置に、赤い水平線を描画
plt.axhline(nu / (nu - 2), color='tomato', linewidth=2)
# x軸ラベル・y軸ラベルの設定
plt.xlabel('sample size')
plt.ylabel('unbiased variance');【実行結果】


4.1.4 不偏性
推定量$${\hat{\theta}}$$の期待値が母数$${\theta}$$に一致することを不偏性と呼び、このような推定量を不偏推定量と呼びます。
数式表現です。
$$
E[\hat{\theta}] = \theta
$$
母平均の不偏推定量
■ 標本平均が母平均の不偏推定量であることをシミュレーション
テキストによると「平均$${\mu}$$の母集団分布に互いに独立に従う確率変数の標本平均は母平均$${\mu}$$の不偏推定量」です。
平均0、分散2の正規分布に従う母集団から無作為抽出されたサンプルサイズ20の標本は、平均0、分散$${2/20=1/10}$$の正規分布に従います。
このことをシミュレーションで確認します。
平均0、分散2の正規分布乱数を20個取得して平均を取る、この処理を20000回繰り返して全体の平均値を算出します。
20000件の標本平均のシミュレーションです!
### 128ページ 正規分布N(0, 2):標本平均が母平均の不偏推定量 その1
## 設定と準備
mu = 0 # 母平均
sigma = np.sqrt(2) # 母標準偏差
n = 20 # サンプルサイズ
iter = 20000 # 標本を得る回数(標本数)
# # 結果を格納するオブジェクト リスト内包表記を利用する場合、変数の準備は不要
# sample_mean = np.zeros(iter)
## シミュレーション
rng = np.random.default_rng(seed=123)
# for文に代えてリスト内包表記を利用
# for i in range(iter):
# sample_mean[i] = rng.normal(size=n, loc=mu, scale=sigma).mean()
sample_mean = np.array(
[rng.normal(size=n, loc=mu, scale=sigma).mean() for _ in range(iter)])
## 結果
sample_mean.mean() # 標本平均の平均【実行結果】
標本平均の平均は母平均0に近似しました。
標本平均は母平均の不偏統計量と言えそうです。

ここからはシミュレーションデータの分布の確認に突入です!
標本分散の標本分散を算出します。
### 129ページ 正規分布N(0, 2):標本平均が母平均の不偏推定量 その2
sample_mean.var(ddof=0) # 標本平均の標本分散【実行結果】
0.1 に近似しました。

20000 個の標本平均のヒストグラムを描きます。
標本平均の平均値の垂直線を併せます。
標本平均が従う平均0、分散 1/10 の正規分布の確率密度関数と重ねます。
### 129ページ 正規分布N(0, 2):標本平均が母平均の不偏推定量 その3 図4.6
# ヒストグラムの描画
plt.hist(sample_mean, bins=30, density=True, ec='white', alpha=0.7)
# 「生成した標本平均」の平均の位置に黒い垂直線を描画
plt.axvline(sample_mean.mean(), color='black', linewidth=4)
# 母平均・母標準偏差の真値による正規分布の確率密度関数の描画
line_x = np.linspace(sample_mean.min(), sample_mean.max(), 1001)
plt.plot(line_x, stats.norm.pdf(line_x, loc=mu, scale=sigma / np.sqrt(n)),
color='tab:red', linewidth=2)
# x軸ラベル・y軸ラベル・タイトルの設定
plt.xlabel('sample_mean')
plt.ylabel('Density')
plt.title('Histogram of sample_mean');【実行結果】
シミュレーションの結果、標本平均の従う分布は、理論値である平均0、分散 1/10 の正規分布に近似することが分かりました。

■ 母集団分布にt分布を仮定して標本平均をシミュレーション
母集団分布にt分布を仮定した場合にも標本平均が母平均の不偏推定量であることをシミュレーションで確かめます。
自由度4のt分布です。平均0、分散2です。
標本平均の標本分布は平均0,分散$${2/20=1/10}$$です。
標本平均の平均をシミュレーションします。
### 130ページ t分布(非正規分布):標本平均が母平均の不偏推定量 その1
## 設定と準備
nu = 4 # t分布自由度。自由度4のt分布の期待値は0、分散は2
mu = 0 # 母平均
sigma = np.sqrt(nu / (nu - 2)) # 母標準偏差
n = 20 # サンプルサイズ
iter = 20000 # 標本を得る回数(標本数)
## シミュレーション
rng = np.random.default_rng(seed=1)
# for文に代えてリスト内包表記を利用
sample_mean = np.array(
[rng.standard_t(size=n, df=nu).mean() for _ in range(iter)])
## 結果
sample_mean.mean() # 標本平均の平均【実行結果】
標本平均の平均は理論値の0に近似します。
母集団分布が自由度4のt分布ときも、標本平均は母平均の不偏統計量と言えそうです。

ここからはシミュレーションデータの分布の確認に突入です!
標本平均の標本分散をシミュレーションします。
### 130ページ t分布(非正規分布):標本平均が母平均の不偏推定量 その2
sample_mean.var(ddof=0) # 標本平均の標本分散【実行結果】
標本平均の標本分散は理論値の$${1/10}$$に近似します。

20000 個の標本平均のヒストグラムを描きます。
標本平均の平均値の垂直線を併せます。
標本平均が従う平均0、分散 1/10 の正規分布の確率密度関数と重ねます。
### 130ページ t分布(非正規分布):標本平均が母平均の不偏推定量 その2 131ページ図4.7
# ヒストグラムの描画
plt.hist(sample_mean, bins=60, density=True, ec='white', alpha=0.7)
# 「生成した標本平均」の平均の位置に黒い垂直線を描画
plt.axvline(sample_mean.mean(), color='black', linewidth=4)
# 母平均・母標準偏差の真値による正規分布の確率密度関数の描画
line_x = np.linspace(sample_mean.min(), sample_mean.max(), 1001)
plt.plot(line_x, stats.norm.pdf(line_x, loc=mu, scale=sigma / np.sqrt(n)),
color='tab:red', linewidth=2)
# x軸ラベル・y軸ラベル・タイトルの設定
plt.xlabel('sample_mean')
plt.ylabel('Density')
plt.title('Histogram of sample_mean');【実行結果】
ヒストグラムの形状は、標本平均の標本分布の理論値である平均0、分散 1/10 の正規分布と似ています。
しかし、テキストは「実はこのとき、標本平均の標本分布は正規分布”ではない”のです」と訴えかけます!

Q-Qプロットでシミュレーションデータが正規分布に近似しているか確認します。
scipy の probplot で Q-Qプロットを描画できます。
### 132ページ Q-Qプロットの描画 132ページ図4.8
stats.probplot(sample_mean, dist='norm', plot=plt)
plt.ylabel('Sample Quantities');【実行結果】
青いデータ点が赤い線に乗っかっている時、データは正規分布に近似していることになります。
この図では、赤い線の両端で、データ点が赤い線から大きく外れています。
つまり、シミュレーションデータは正規分布に近似していない、ということです。
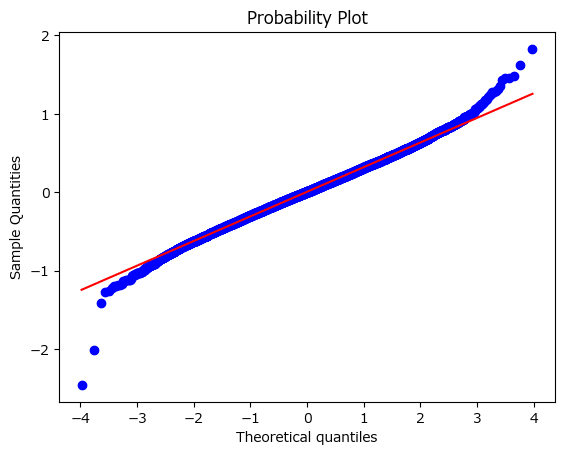
母集団分布が正規分布でないとき、標本平均が従う標本分布が平均$${\mu}$$、分散$${\sigma^2/n}$$の正規分布に従うとは限らない、ということのようです。
■ 母集団分布に標準コーシー分布を仮定して標本平均をシミュレーション
母集団が標準コーシー分布の場合、標本平均は母平均の不偏推定量にはならないそうです。
シミュレーションで確かめます。
### 自由度1のt分布=標準コーシー分布の標本平均 不偏性の確認
## 設定と準備
nu = 1 # t分布自由度。自由度1のt分布の期待値・分散なし
mu = 0 # 母平均
sigma = np.sqrt(nu / (nu - 2)) # 母標準偏差
n = 20 # サンプルサイズ
iter = 20000 # 標本を得る回数(標本数)
## シミュレーション
rng = np.random.default_rng(seed=1)
# for文に代えてリスト内包表記を利用
sample_mean = np.array(
[rng.standard_t(size=n, df=nu).mean() for _ in range(iter)])
## 結果
print('標本平均の平均', sample_mean.mean()) # 標本平均の平均
print('標本平均の不偏分散', sample_mean.var(ddof=0)) # 標本平均の標本分散
# ヒストグラムの描画
plt.hist(sample_mean, bins=60, density=True, ec='white', alpha=0.7)
# 「生成した標本平均」の平均の位置に黒い垂直線を描画
plt.axvline(sample_mean.mean(), color='black', linewidth=4)
# 母平均・母標準偏差の真値による正規分布の確率密度関数の描画
line_x = np.linspace(sample_mean.min(), sample_mean.max(), 1001)
plt.plot(line_x, stats.norm.pdf(line_x, loc=mu, scale=sigma / np.sqrt(n)),
color='tab:red', linewidth=2)
# x軸ラベル・y軸ラベル・タイトルの設定
plt.xlabel('sample_mean')
plt.ylabel('Density')
plt.title('Histogram of sample_mean')
plt.show()
# Q-Qプロットの描画
stats.probplot(sample_mean, dist='norm', plot=plt)
plt.ylabel('Sample Quantities');【実行結果】
標本平均の平均は0から乖離している感じです。
テキストの通り、母集団分布が標準コーシー分布のとき、不偏性が成立しないようです。




母分散の不偏推定量
■ 不偏分散が母分散の不偏推定量であることをシミュレーション
テキストによると「平均$${\mu}$$の母集団分布に互いに独立に従う確率変数の不偏分散は母分散$${\sigma^2}$$の不偏推定量」です。
しかし、標本分散は母分散の不偏推定量ではありません。
まずは不偏分散の不偏性を確認しましょう。
自由度4のt分布乱数20個を20000回生成して不偏分散をシミュレーションします。
母分散は2です。
### 133ページ t分布(非正規分布):不偏分散が母分散の不偏推定量 その1 図4.9
## 設定と準備
nu = 4 # t分布自由度
n = 20 # サンプルサイズ
iter = 20000 # 標本を得る回数(標本数)
## シミュレーション
rng = np.random.default_rng(seed=11)
# for文に代えてリスト内包表記を利用 var(ddof=1)は不偏分散
sample_var = np.array(
[rng.standard_t(size=n, df=nu).var(ddof=1) for _ in range(iter)])
## 結果 ヒストグラムの描画
plt.hist(sample_var, bins=200, alpha=0.7)
# x軸ラベル・y軸ラベル・タイトルの設定
plt.xlabel('sample_var')
plt.ylabel('Frequency')
plt.title('Histogram of sample_var');【実行結果】
不偏分散の分布は0から5の間に集中している感じです。

### 133ページ 生成した20000個の不偏分散の平均
sample_var.mean()【実行結果】
不偏分散の平均は母分散2に近似しました。
不偏分散は母分散の不偏統計量と言えそうです。

■ 標本分散が母分散の不偏推定量ではないことをシミュレーション
続いて標本分散が不偏性を持たないことを確認しましょう。
### 134ページ t分布(非正規分布):標本分散と不偏性 その1図4.10
## 設定と準備
nu = 4 # t分布自由度
n = 20 # サンプルサイズ
iter = 20000 # 標本を得る回数(標本数)
## シミュレーション
rng = np.random.default_rng(seed=11)
# for文に代えてリスト内包表記を利用 var(ddof=0)は標本分散
sample_var = np.array(
[rng.standard_t(size=n, df=nu).var(ddof=0) for _ in range(iter)])
## 結果 ヒストグラムの描画
plt.hist(sample_var, bins=200, alpha=0.7)
# x軸ラベル・y軸ラベル・タイトルの設定
plt.xlabel('sample_var')
plt.ylabel('Frequency')
plt.title('Histogram of sample_var');【実行結果】
不偏分散の分布に良く似ています。。。

### 134ページ 生成した20000個の標本分散の平均
sample_var.mean()【実行結果】
若干2からずれています。
標本分散は母分散の不偏統計量ではなさそうです。

■ 不偏分散の正の平方根が母標準偏差の不偏性かをシミュレーション
不偏分散の正の平方根は母標準偏差の不偏統計量ではないそうです。
シミュレーションします。
自由度4のt分布乱数で検証します。
母標準偏差は$${\sqrt{2} \fallingdotseq 1.414}$$です。
### 135ページ t分布(非正規分布)
# 不偏分散の正の平方根は母標準偏差の不偏推定量ではない
## 設定と準備
nu = 4 # t分布自由度
n = 20 # サンプルサイズ
iter = 20000 # 標本を得る回数(標本数)
## シミュレーション
rng = np.random.default_rng(seed=11)
# for文に代えてリスト内包表記を利用 std(ddof=1)は不偏分散の平方根
sample_sd = np.array(
[rng.standard_t(size=n, df=nu).std(ddof=1) for _ in range(iter)])
## 結果
sample_sd.mean()【実行結果】
1.414 からずれています。
不偏分散の平方根は母標準偏差の不偏統計量ではなさそうです。


母相関係数の不偏推定量
標本相関係数$${R}$$が母相関係数$${\rho}$$の不偏統計量かどうかを確かめるシミュレーションです。
テキストの通り、母相関係数が$${-0.5,0,0.8}$$の3つのケースを確かめます。
2変量正規分布乱数20個から相関係数をとることを20000回シミュレーションします。
### 135ページ 標本相関係数が母相関係数の不偏推定量かどうかの検証
## 設定と準備
rho_vec = np.array([-0.5, 0, 0.8]) # 3通りの母相関係数
mu_vec = np.array([0, 5]) # 2変量の母平均ベクトル
sigma_vec = np.array([10, 20]) # 2変量の母標準偏差ベクトル
n = 20 # サンプルサイズ
iter = 20000 # 標本を得る回数(標本数)
# 描画領域の設定
plt.figure(figsize=(8, 6))
# 乱数生成器・乱数シードの設定
rng = np.random.default_rng(seed=11)
# 3通りの母相関係数で2変量正規分布乱数を生成し、相関係数を算出して可視化
for i in range(len(rho_vec)):
## 相関行列の作成
rho_matrix = np.array([[1, rho_vec[i]],
[rho_vec[i], 1]])
## リスト内包表記でiter回分の相関係数を算出
r = np.array([
# 相関係数算出corrcoefをiter回繰り返す
np.corrcoef(
# n個の2変量正規分布乱数をn行×2列生成して転置T
rng.multivariate_normal(
size=n, mean=mu_vec,
cov=np.diag(sigma_vec) @ rho_matrix @ np.diag(sigma_vec)).T
)[0, 1]
for _ in range(iter)])
## 可視化
# 描画領域の追加
ax = plt.subplot(2, 2, i + 1)
# 乱数rのヒストグラムの描画
ax.hist(r, bins=40, color='tab:blue', ec='white', alpha=0.7)
# 生成した相関係数の平均の位置に垂直線を引く
ax.axvline(r.mean(), color='tab:red', linewidth=3)
# タイトル・x軸ラベル・y軸ラベルの設定
ax.set(title=rf'$\rho$ = {rho_vec[i]}, mean = {r.mean():.4f}',
xlabel='r', ylabel='Frequecy')
plt.tight_layout();【実行結果】
標本相関係数$${R}$$の平均値は母相関係数$${\rho}$$に近似しています。
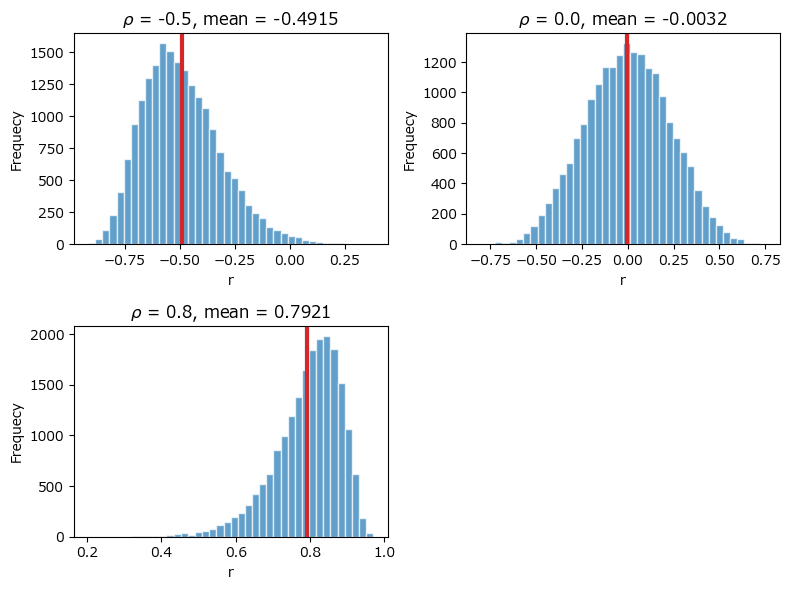
テキストは標本相関係数の分布の形状に着目しています。
母相関係数$${\rho}$$が$${-0.5, 0.8}$$のとき、分布の形状が偏っています。
テキストによると標本相関係数$${R}$$の期待値と母相関係数$${\rho}$$が近似的に次の式のような関係があるため、とのことです。
$$
E[R] \approx \rho - \cfrac{\rho\ (1 - \rho^2)}{2n} \\
$$

4.1.5 有効性
複数存在する可能性のある不偏推定量のうち、最も分散$${V[\hat{\theta}]}$$が小さな推定量$${\hat{\theta}}$$を有効推定量と呼ぶそうです。
母平均の有効推定量
母集団分布が正規分布のとき、標本平均と標本中央値は母平均の不偏推定量です。
母集団分布が標準正規分布のケースで標本平均と標本中央値の分散を確認しましょう。
■ 母集団分布が標準正規分布のケースで標本平均と標本中央値をシミュレーション
まず標本平均と標本中央値の期待値が0であることを確認します。
### 138ページ 標準正規分布の有効推定量:標本平均と標本中央値1
## 設定と準備
n = 20 # サンプルサイズ
iter = 20000 # 標本を得る回数(標本数)
## シミュレーション
rng = np.random.default_rng(seed=3)
# for文に代えてリスト内包表記を利用 rng.standard_normalは標準正規分布乱数
sample = np.array([rng.standard_normal(size=n) for _ in range(iter)])
sample_mean = np.mean(sample, axis=1) # 標本平均
sample_median = np.median(sample, axis=1) # 標本中央値
## 結果
# 標本平均の平均。母平均の不偏統計量であることのシミュレーション
sample_mean.mean()【実行結果】
標本平均の平均は0に近似します。

### 138ページ 標準正規分布の有効推定量:標本平均と標本中央値2
#標本中央値の平均。母平均の不偏統計量であることのシミュレーション
sample_median.mean()【実行結果】
標本中央値の平均は0に近似します。
標本平均と標本中央値のシミュレーションで得た値のヒストグラムを描画します。
### 138ページ 標準正規分布の有効推定量:標本平均と標本中央値3 139ページ図4.12
# 描画領域の設定
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(8, 3), sharex=True, sharey=True)
# 標本平均のヒストグラムの描画
ax1.hist(sample_mean, bins=40, color='tab:blue', ec='white', alpha=0.7)
ax1.set(xlabel='sample_mean', ylabel='Frequency', title='Sample mean')
# 標本中央値のヒストグラムの描画
ax2.hist(sample_median, bins=40, color='tab:blue', ec='white', alpha=0.7)
ax2.set(xlabel='sample_median', ylabel='Frequency', title='Sample median')
# 全体修飾
plt.tight_layout();【実行結果】
左が標本平均の標本分布、右が標本中央値の標本分布です。
テキストの通り「標本平均のほうがバラツキが小さい=分散が小さい」感じです。

標本平均と標本中央値の分散を計算します。
### 139ページ 標準正規分布の有効推定量:標本平均と標本中央値4
sample_mean.var(ddof=1) # 標本平均の分散(不偏分散)【実行結果】
標本平均の分散です。

### 139ページ 標準正規分布の有効推定量:標本平均と標本中央値4
sample_median.var(ddof=1) # 標本中央値の分散(不偏分散)【実行結果】
標本中央値の分散です。

標本平均の分散のほうが小さいです。
テキストによると「母集団分布が正規分布のとき、標本平均は母平均の有効推定量であることがわかっている」とのことです。
■ 母集団分布が自由度3のt分布のときの標本平均・標本中央値の分散
またテキストは「母集団分布が小さい自由度を持つt分布のとき、標本平均よりも標本中央値の方が分散$${V[\hat{\theta}]}$$が小さくなる」とのこと。
シミュレーションの出番です!
自由度3のt分布の乱数20個で標本平均と標本中央値を算出する処理を10000回繰り返します。
### 140ページ t分布の有効推定量:標本平均と標本中央値1
## 設定と準備
n = 20 # サンプルサイズ
iter = 10000 # 標本を得る回数(標本数)
nu = 3 # 自由度
## シミュレーション
rng = np.random.default_rng(seed=3)
# for文に代えてリスト内包表記を利用
sample = np.array([rng.standard_t(size=n, df=nu) for _ in range(iter)])
sample_mean = np.mean(sample, axis=1) # 標本平均
sample_median = np.median(sample, axis=1) # 標本中央値
## 結果
print('標本平均の分散 :', sample_mean.var(ddof=1)) # 標本平均の分散(不偏分散)
print('標本中央値の分散:', sample_median.var(ddof=1)) # 標本中央値の分散(不偏分散)【実行結果】
たしかに標本中央値の方が分散が小さいです!


4.1.6 サンプルサイズと標本分布の関係
サンプルサイズと標本分布の関係を標本平均のシミュレーションで探ります。
■ 母集団分布が正規分布、サンプルサイズ4のシミュレーション
母集団分布が平均0、分散2の正規分布を仮定すると、サンプルサイズ$${n}$$の標本平均の標本分布は平均0、分散$${2/n}$$の正規分布になります。
まずはサンプルサイズ4でシミュレーションします。
### 141ページ サンプルサイズと正規分布:サンプルサイズが小さいケース 142ページ図4.13
## 設定と準備
mu = 0 # 母平均
sigma = np.sqrt(2) # 母標準偏差
n = 4 # サンプルサイズ
iter = 20000 # 標本を得る回数(標本数)
## シミュレーション
rng = np.random.default_rng(seed=0)
# for文に代えてリスト内包表記を利用
sample_mean = np.array(
[rng.normal(size=n, loc=mu, scale=sigma).mean() for _ in range(iter)])
## 結果
# 描画領域の設定
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(8, 3))
# ヒストグラムの描画
ax1.hist(sample_mean, bins=50, density=True,
color='tab:blue', ec='white', alpha=0.7)
# 母平均・母標準偏差がパラメータの正規分布の確率密度関数の描画
line_x = np.linspace(sample_mean.min(), sample_mean.max(), 1001)
ax1.plot(line_x, stats.norm.pdf(line_x, loc=mu, scale=sigma / np.sqrt(n)),
linewidth=2, color='tab:red')
# x軸ラベル・y軸ラベル・タイトルの設定
ax1.set(xlabel='sample_mean', ylabel='Density', title=f'n={n}')
# Q-Qプロットの描画
stats.probplot(sample_mean, dist='norm', plot=ax2)
ax2.set(ylabel='Sample Quantities', title=f'n={n}')
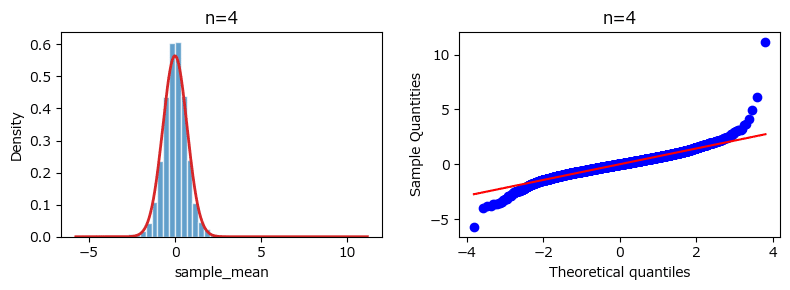
plt.tight_layout();【実行結果】
サンプルサイズが4(小さい)場合であっても、標本分布は平均0、分散$${2/n=2/4=1/2}$$の正規分布に類似しています。

■ 中心極限定理のシミュレーション
今度は、母集団分布が自由度4のt分布を仮定します。
中心極限定理をシミュレーションします。
【中心極限定理】
平均$${\mu}$$、分散$${\sigma^2}$$の母集団分布に互いに独立に従う確率変数の標本平均は、サンプルサイズ$${n}$$が大きくなるにつれて、平均$${\mu}$$、標準偏差$${\sigma/\sqrt{n}}$$の正規分布に近似する。
サンプルサイズを$${4, 10, 100}$$のケースでシミュレーションします。
### 142ページ サンプルサイズとt分布:サンプルサイズ3ケース 143ページ図4.14
## 設定と準備
nu = 4 # 自由度 このとき、t分布の期待値は0, 分散は2
mu = 0 # 母平均
sigma = np.sqrt(nu / (nu - 2)) # 母標準偏差
n_list = [4, 20, 100] # 3つのサンプルサイズ
iter = 10000 # 標本を得る回数(標本数)
## シミュレーション
rng = np.random.default_rng(seed=123)
# 3つのサンプルサイズごとにシミュレーションと描画を繰り返し処理
for n in n_list:
# for文に代えてリスト内包表記を利用
sample_mean = np.array(
[rng.standard_t(size=n, df=nu).mean() for _ in range(iter)])
## 結果
# 描画領域の設定
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(8, 3))
# ヒストグラムの描画
ax1.hist(sample_mean, bins=50, density=True,
color='tab:blue', ec='white', alpha=0.7)
# 母平均・母標準偏差がパラメータの正規分布の確率密度関数の描画
line_x = np.linspace(sample_mean.min(), sample_mean.max(), 1001)
ax1.plot(line_x, stats.norm.pdf(line_x, loc=mu, scale=sigma / np.sqrt(n)),
linewidth=2, color='tab:red')
# x軸ラベル・y軸ラベル・タイトルの設定
ax1.set(xlabel='sample_mean', ylabel='Density', title=f'n={n}')
# Q-Qプロットの描画
stats.probplot(sample_mean, dist='norm', plot=ax2)
ax2.set(ylabel='Sample Quantities', title=f'n={n}')
plt.tight_layout()
plt.show()【実行結果】
右側のQ-Qプロットに注目します。
サンプルサイズが大きくなるにつれて、データ点は赤い線にうまく乗ってきており、正規分布に近似する様子がわかります。
テキストによると「標本平均の分位点は平均0,分散$${2\n}$$の正規分布の理論的な分位点に近づいています」。
中心極限定理をシミュレーションで確かめることができました。


今回の写経は以上です。
シリーズの記事
次の記事
前の記事
目次
ブログの紹介
note で7つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
Python、EXCELのサンプルコードの配布もあります。
2.実験!たのしいベイズモデリング1&2をPyMC Ver.5で
書籍「たのしいベイズモデリング」・「たのしいベイズモデリング2」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは R言語+Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう!
3.実験!岩波データサイエンス1のベイズモデリングをPyMC Ver.5で
書籍「実験!岩波データサイエンスvol.1」の4人のベイジアンによるベイズモデルを PyMC Ver.5で描いて分析します。
この書籍はベイズプログラミングのイロハをざっくりと学ぶことができる良書です。
楽しくPyMCモデルを動かして、ベイズと仲良しになれた気がします。
みなさんもぜひぜひPyMCで動かして、一緒に遊んで学びましょう!
4.楽しい写経 ベイズ・Python等
ベイズ、Python、その他の「書籍の写経活動」の成果をブログにします。
主にPythonへの翻訳に取り組んでいます。
写経に取り組むお仲間さんのサンプルコードになれば幸いです🍀
5.RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析をPythonとPyMC Ver.5 で実践します。
この書籍には時系列分析のテーマが盛りだくさん!
時系列分析の懐の深さを実感いたしました。
大好きなPythonで楽しく時系列分析を学びます。
6.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
統計・データサイエンス書籍にまつわる記事が多いです。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
7.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。
最後までお読みいただきまして、ありがとうございました。
