
「数値シミュレーションで読み解く統計のしくみ」をPythonで写経 ~ 第3章3.1「確率変数と確率分布」
第3章「乱数生成シミュレーションの基礎」
書籍の著者 小杉考司 先生、紀ノ定保礼 先生、清水裕士 先生
この記事は、テキスト「数値シミュレーションで読み解く統計のしくみ」第3章「乱数生成シミュレーションの基礎」3.1節「確率変数と確率分布」の Python写経活動 を取り扱います。
今回からシミュレーションの核になる乱数生成に取り組みます。
確率分布との親交(理解)を深めつつ、確率分布から生み出される乱数の1つ1つに思いを寄せて、コードをPython写経します。
R の基本的なプログラム記法はざっくり Python の記法と近いです。
コードの文字の細部をなぞって、R と Python の両方に接近してみましょう!
ではテキストを開いて準備体操の旅に出発です🚀

はじめに
テキスト「数値シミュレーションで読み解く統計のしくみ」のご紹介
このシリーズは書籍「数値シミュレーションで読み解く統計のしくみ〜Rでためしてわかる心理統計」(技術評論社、「テキスト」と呼びます)の Python写経です。
テキストは、2023年9月に発売され、副題「Rでためしてわかる心理統計」のとおり、統計処理に定評のある R の具体的なコードを用いて、心理統計の理解に役立つ数値シミュレーションを実践する素晴らしい書籍です。
引用表記
この記事は、出典に記載の書籍に掲載された文章及びコードを引用し、適宜、掲載文章とコードを改変して書いています。
【出典】
「数値シミュレーションで読み解く統計のしくみ〜Rでためしてわかる心理統計」初版第1刷、著者 小杉考司・紀ノ定保礼・清水裕士、技術評論社
記事中のイラストは、「かわいいフリー素材集いらすとや」さんのイラストをお借りしています。
ありがとうございます!
3.1 確率変数と確率分布
テキストは「確率変数」の解説からはじまります。
確率変数はざっくり「確率分布による縛りを持つ変数」です。
確率分布にはいろんなものがあります。
そこでテキストは、確率変数の実現値が確率的に定まる様子を「乱数生成」を使い、主要な確率分布をカバーしながら、丁寧に確認していきます。
この記事は Jupyter Notebook 形式(拡張子 .ipynb)でPythonコードを書きます。
概ね確率分布の特性値算出には scipy.stats を用い、乱数生成には numpy.random.generator を用いるようにしています。
主に利用するライブラリをインポートします。
### インポート
# 数値計算
import numpy as np
# データフレーム
import pandas as pd
# 確率・統計
import scipy.stats as stats
# 描画
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'Meiryo'
3.1.1 確率変数
■ サイコロ振りのシミュレーション
いきなりシミュレーションです!
サイコロ振りのシミュレーションです。
1~6の整数からランダムに8個の数値を取り出して表示します。
ランダムに取り出すアクションは「乱数」で対応します。
### 63ページ サイコロ
# サイコロを振る回数
iter = 8
# サイコロを表すオブジェクトに1~6の整数を代入
dice = list(range(1, 7)) # リスト型
# 乱数生成器の設定
rng = np.random.default_rng(seed=123)
# サイコロを8回振って結果を表示
for i in range(iter):
# diceからランダムにいずれかの数値を抽出して、xに代入
x = rng.choice(a=dice, replace=True)
# xに代入された数値(実現値)を表示
print(x)【実行結果】
1~6の整数がランダムに並んでいます。
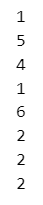
【コード補足】numpy random generator の乱数生成
1.rngって何者?
「rng = np.random.default_rng(seed=123)」で rng に乱数生成のアビリティを授けます!乱数シードは123です。呪文の定型文です!
以後、乱数を生成するときには、rng.choice() のように rng に指示をします。
2.choiceとは?
rng.choice(a=dice, replace=True)は、引数 a に指定した変数 dice の値からランダムに選択(choice)するコードです。
変数 dice には1~6までの整数値が入っているので「サイコロの目をランダムに選ぶ」ということを実現できています。
replace 引数で True を指定すると復元抽出(同じ値を何度も抽出可能)を行います。
■ サイコロの出た目の平均値
続くシミュレーションは、サイコロの目の平均値(標本平均)の採取です。
サイコロを2回振って平均をとります。
choice() の引数 size で2を指定することで、サイコロを2個同時に振るかのごとく、一度に2個の乱数を生成できます。
choice() の引数 replace で True を指定しているので、同じ目を何度も出せます。
これを8回繰り返します。
### 64ページ サイコロを2回振って出た目の平均値を取得
iter = 8 # 平均値を求める回数
n = 2 # 復元抽出する個数
dice = list(range(1, 7)) # サイコロの目
# 乱数生成器の設定
rng = np.random.default_rng(seed=123)
for i in range(iter):
# diceからランダムにn個の数値を復元抽出し、それらの平均をxに代入
x = rng.choice(a=dice, size=2, replace=True).mean()
# xに代入された数値(平均値)を表示
print(x)【実行結果】

■ 出目の確率が均一でない場合(イカサマサイコロ)
まだまだシミュレーションは続きます。
choice() の引数 p に各要素の確率をバラバラに設定することで、イカサマサイコロが出来上がります!
テキストの例では、1~4の目の出る確率が 0.1、5と6の目が出る確率が 0.3 です。
5と6が他の目よりも3倍出やすい設定です。
### 66ページ 出目確率が均一でないサイコロ振りのシミュレーション
## 設定と準備
n = 1000 # サイコロを振る回数
dice = list(range(1, 7)) # 観測しうる値
rng = np.random.default_rng(seed=123) # 乱数生成器の設定
## シミュレーション
# diceからランダムにn個の数値を非復元抽出
x = rng.choice(a=dice, size=n, replace=True, p=[0.1, 0.1, 0.1, 0.1, 0.3, 0.3])
# サイコロの目(dice_num)ごとの頻度(counts)を算出
dice_num, counts = np.unique(x, return_counts=True)
## データをpandasデータフレームに変換
pd.DataFrame(counts.reshape(1, -1), columns=dice_num)【実行結果】
1000回のシミュレーションの結果、各目の出た回数はおよそ「1:1:1:1:3:3」になりました。


サイコロを題材にしたシミュレーション、面白かったですね!
コラム:非復元抽出
choice の引数 replace に False を設定すると「非復元抽出」になります。
つまり、1度出た目は二度と出せなくなるのです。
次のコードは6つのサイコロの目を非復元抽出で8回振る時、6回振った時点で全目が出尽くすため、7回目の振りで選べる目が無くなり、エラーになります。
### 65ページ サイコロを2回振って出た目の平均値を取得 エラーが発生する
### 設定と準備
n = 8 # 非復元抽出する個数
dice = list(range(1, 7)) # サイコロの目
rng = np.random.default_rng(seed=123) # 乱数生成器の設定
# diceからランダムにn個の数値を非復元抽出
x = rng.choice(a=dice, size=n, replace=False)
print(x)【実行結果】


3.1.2 確率分布
この先は確率分布と確率とのふれあいコーナーです。
1.確率質量関数の例(離散一様分布)
離散一様分布の確率:確率質量関数を算出します。
離散一様分布には scipy.stats の randint を使用し、.pmf とすることで確率質量関数を取得できます。
テキストにならって、1~6の整数(サイコロの目)に見立てて特定の目がでる確率を算出します。
最初に1の目の出る確率です。
### 69ページ scipy.statsで離散一様分布randintの確率質量関数を計算
stats.randint.pmf(k=1, low=1, high=6+1) # highは+1【実行結果】
$${1/6 = 0.166 \cdots}$$です、合ってます!

続いて0と1が出る確率です。
サイコロの目に0は無いので、実質的に1が出る確率になると予測できます!
### 70ページ scipy.statsで離散一様分布randintの確率質量関数を計算
stats.randint.pmf(k=[0, 1], low=1, high=6+1).sum() # highは+1【実行結果】

最後に1~6の全ての目が出る確率です。
### 70ページ scipy.statsで離散一様分布randintの確率質量関数を計算
stats.randint.pmf(k=range(1, 7), low=1, high=6+1).sum() # highは+1【実行結果】
サイコロの全部の目の確率=全確率=1です(若干端数が。。。)


2.確率密度関数の例(正規分布)
標準正規分布の確率密度関数を描画します。
テキストの図3.4に相当します。
### 71ページ 図3.4 標準正規分布の確率密度関数の描画
plt.figure(figsize=(6, 3))
xval = np.linspace(-5, 5, 1001)
plt.plot(xval, stats.norm.pdf(xval, loc=0, scale=1))
plt.xlabel('x')
plt.ylabel('density');【実行結果】
「左右対称のベル型の形状」が正規分布の確率密度関数の特徴です。

■ 連続型確率分布の確率密度関数を積分すると確率が分かる
テキストはしばらく、標準正規分布の確率変数のさまざまな範囲に関して、確率を算出するテーマに取り組みます。
同じ描画処理を繰り返すので、描画関数を関数化します。
### 図3.5等の描画に利用する関数を定義
def plot_std_normal(lower, upper, xmin=-5, xmax=5, ax=None):
## 設定
# 確率変数xの値(x軸の値)
xval = np.linspace(xmin, xmax, 1001)
# 積分範囲の確率変数xの値(x軸の値)
xval_draw = np.linspace(lower, upper, 1001)
# 標準正規分布オブジェクトの作成
std_norm = stats.norm(loc=0, scale=1)
## 描画処理
# 描画領域の設定
if ax == None:
ax = plt.subplot()
# 確率密度関数の描画
ax.plot(xval, std_norm.pdf(xval))
# 積分範囲の塗りつぶし
ax.fill_between(xval_draw, 0, std_norm.pdf(xval_draw), alpha=0.3)
# 積分範囲の下端の垂直線の描画
ax.vlines(lower, 0, std_norm.pdf(lower), linewidth=0.5)
# 積分範囲の上端の垂直線の描画
ax.vlines(upper, 0, std_norm.pdf(upper), linewidth=0.5)
# 積分範囲のx軸=0の水平線線の描画
ax.hlines(0, lower, upper, linewidth=0.5)
# 修飾
ax.set(xlabel='x', ylabel='density')
return ax■ 確率変数$${X}$$が$${-0.5 \leq X \leq 0.5}$$の区間の場合
上記区間を青色で塗りつぶしした確率密度関数を描画してみましょう。
### 71ページ 図3.5の描画
# 積分範囲
lower = -0.5
upper = 0.5
# 描画処理
plt.figure(figsize=(6, 3))
plot_std_normal(lower, upper);【実行結果】

テキストは標準正規分布の確率密度関数を数値積分することで確率を求めています。
テキストに追随します。
数値積分には scipy の integrate を利用します。
### scipyの積分ライブラリのインポート
from scipy import integratescipy.stats にて標準正規分布オブジェクトを作成します。
### 標準正規分布オブジェクトの生成
std_norm = stats.norm(loc=0, scale=1)確率変数$${X}$$が$${-0.5 \leq X \leq 0.5}$$のときの確率を数値積分で算出します。
### 71ページ 標準正規分布の確率計算:数値積分計算
# 数値積分の実行(積分値, 誤差推定値)
integrate.quad(func=std_norm.pdf, a=-0.5, b=0.5)【実行結果】
カッコの左が積分値、右が計算誤差推定値です。
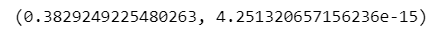
■ 確率変数$${X}$$が$${1 \leq X \leq 2}$$の区間の場合
上記区間を青色で塗りつぶしした確率密度関数を描画します。
### 72ページ 図3.6の描画
# 積分範囲
lower = 1
upper = 2
# 描画処理
plt.figure(figsize=(6, 3))
plot_std_normal(lower, upper);【実行結果】

確率変数$${X}$$が$${1 \leq X \leq 2}$$のときの確率を数値積分で算出します。
### 72ページ 標準正規分布の確率計算:数値積分計算
integrate.quad(func=std_norm.pdf, a=1, b=2)【実行結果】

■ 確率変数$${X}$$が$${X \leq 1.96}$$の区間の場合
上記区間を青色で塗りつぶしした確率密度関数を描画します。
### 72ページ 図3.7の描画
# 積分範囲
lower = -5
upper = -1.96
# 描画処理
# 描画処理
plt.figure(figsize=(6, 3))
plot_std_normal(lower, upper);【実行結果】
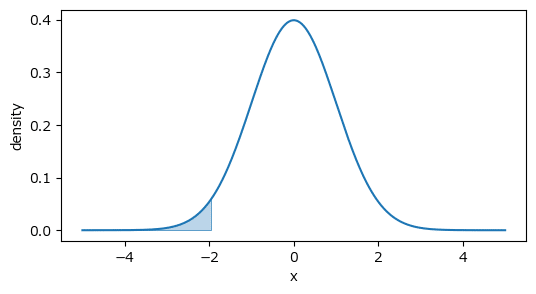
確率密度関数の下限から一定区間の確率を求める場合、累積分布関数で算出することができます。
scipy.stats の norm.cdf() で累積分布関数を算出できます。
確率変数$${X}$$が$${X \leq -1.96}$$のときの確率を累積分布関数から算出します。
### 73ページ 標準正規分布の確率計算:累積分布関数 確率変数x=1.96
std_norm.cdf(x=-1.96)【実行結果】
およそ$${0.025}$$です。

ちなみに、数値積分で算出してもほぼ同じ値になりました。
### 標準正規分布の確率計算:数値積分計算
integrate.quad(func=std_norm.pdf, a=-np.inf, b=-1.96)【実行結果】

■ 累積分布関数でいくつか計算
さきほどの確率変数$${X}$$が$${-0.5 \leq X \leq 0.5}$$の区間の場合の確率を累積分布関数の引き算で算出します。
### 73ページ 標準正規分布の確率計算:累積分布関数 引き算
std_norm.cdf(x=0.5) - std_norm.cdf(x=-0.5)【実行結果】

上限が$${\infty}$$の場合の累積確率を累積分布関数で求めます。
### 73ページ 標準正規分布の確率計算:累積分布関数 確率変数x=無限大
std_norm.cdf(x=np.inf)【実行結果】
全確率1になりました。

■ 確率変数$${X}$$が$${1.96 \leq X}$$の区間の場合
全確率1から、確率変数1.96の累積分布関数を差し引くと、$${1.96 \leq X}$$の確率を算出できます。
### 73ページ 標準正規分布の確率計算:累積分布関数 上側確率2.5%
1 - std_norm.cdf(x=1.96)【実行結果】
ほぼ$${0.025}$$になりました。
標準正規分布に従う確率変数の上側$${2.5\%}$$点は$${1.96}$$です。

■ 確率変数$${X}$$が$${X = 1}$$の区間の場合
今までは確率変数の区間(2点間)を見てきました。
確率変数$${X}$$が$${X = 1}$$のように1点の場合の確率はどうなるでしょう?
### 74ページ 図3.10の描画 確率変数1点の積分 x=1
# 積分範囲
lower = 1
upper = 1
# 描画処理
# 描画処理
plt.figure(figsize=(6, 3))
plot_std_normal(lower, upper);【実行結果】

### 74ページ 標準正規分布の確率計算:累積分布関数 x=1
std_norm.cdf(x=1) - std_norm.cdf(x=1)【実行結果】
0です。

■ 正規分布の平均パラメータと標準偏差パラメータを変える
平均パラメータを変えると左右にシフトします。
標準偏差パラメータを変えると、ベル型が尖ったり潰れたりします。
### 75ページ パラメータμ、σを変える 76ページ図3.11の描画
## パラメータの設定
mus = [0, 0, 2] # 平均パラメータμ
sigmas = [1, 2, 1] # 標準偏差パラメータσ
styles = ['-', '--', ':'] # 線の種類
xval = np.linspace(-5, 5, 1001) # x軸の値
## 描画処理
# 描画領域の設定
plt.figure(figsize=(6, 3))
# 3つの確率密度関数を繰り返し描画
for (mu, sigma, style) in zip(mus, sigmas, styles):
## stats.norm.pdfで確率密度関数を算出して描画
plt.plot(xval, stats.norm.pdf(xval, loc=mu, scale=sigma),
linestyle=style, label=rf'$\mu$={mu}, $\sigma$={sigma}')
# 修飾
plt.xlabel('x')
plt.ylabel('density')
plt.legend();【実行結果】

■ 正規分布のパラメータを変えると累積確率も変わる
正規分布の平均パラメータ、標準偏差パラメータを変えたときに、確率変数$${X=1.96}$$の累積確率も変わります。
### 76ページ 標準正規分布の累積確率 loc:平均, scale:標準偏差
stats.norm.cdf(x=-1.96, loc=0, scale=1)【実行結果】

### 76ページ μ=0, σ=2の正規分布の累積確率
stats.norm.cdf(x=-1.96, loc=0, scale=2)【実行結果】

### 76ページ μ=2, σ=1の正規分布の累積確率
stats.norm.cdf(x=-1.96, loc=2, scale=1)【実行結果】

■ 分位点(パーセンタイル値)
累積確率が$${p}$$になるような確率変数の値を分位点、パーセンタイル値と呼ぶそうです。
scipy.stats では .ppf でパーセンタイル値を算出できます。
### 77ページ 標準正規分布の2.5パーセンタイル値
stats.norm.ppf(q=0.025, loc=0, scale=1)【実行結果】

### 77ページ μ=0, σ=2の正規分布の16.354305932769236パーセンタイル値
stats.norm.ppf(q=0.16354305932769236, loc=0, scale=2)【実行結果】

### 76ページ μ=2, σ=1の正規分布の0.003.747488169107342パーセンタイル値
stats.norm.ppf(q=3.747488169107342e-05, loc=2, scale=1)【実行結果】
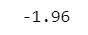

3.1.4 さまざまな確率分布に従う乱数の生成
大きなシミュレーションに進みます。
■ 連続一様分布乱数
範囲$${[1, 6)}$$(6を含まない)の連続一様分布の乱数を5個作成します。
### 78ページ 一様分布に従う乱数
rng = np.random.default_rng(seed=123)
rng.uniform(size=5, low=1, high=6) # 範囲[1, 6)・・・ 6は含まれない【実行結果】

■ モンテカルロ法で標準正規分布の確率を算出
テキストは、一様分布乱数を大量に生成して、標準正規分布の$${-1.96 \leq X \leq 1.96}$$の区間の確率を求めるシミュレーションに移ります。
おさらい:数値積分を用いた確率算出
### 79ページ 標準正規分布の確率計算:数値積分計算
integrate.quad(func=std_norm.pdf, a=-1.96, b=1.96)【実行結果】

おさらい:累積分布関数を用いた確率算出
### 79ページ 標準正規分布の確率確率:累積分布関数の引き算
std_norm.cdf(x=1.96) - std_norm.cdf(x=-1.96)【実行結果】

おさらい:標準正規分布の$${-1.96 \leq X \leq 1.96}$$の区間の可視化
### 79ページ 図3.12 標準正規分布における -1.96 < X 1.96 の区間
# 積分範囲
lower = -1.96
upper = 1.96
# 描画処理
# 描画処理
plt.figure(figsize=(6, 3))
plot_std_normal(lower, upper);【実行結果】


シミュレーションの概要は次のとおりです。
・確率密度関数の青塗り部分を囲う長方形を設定
・長方形めがけて大量の乱数を生成
・乱数のうち青塗りの部分に該当する個数をカウント
・生成乱数の全数に占める青塗り部分の乱数の数の割合を算出
・長方形の面積を加味して、青塗り部分の面積=確率を算出
長方形を描画するライブラリをインポートします。
### 長方形を描画するmatplotlibのライブラリをインポート
import matplotlib.patches as patches確率密度関数の青塗り部分を含む長方形(赤枠)を描きます。
### 80ページ 図3.13 標準正規分布と長方形の描画
## 積分範囲の設定
lower = -1.96
upper = 1.96
## 描画処理
# 描画領域の設定
fig, ax = plt.subplots(figsize=(6, 3))
# 標準正規分布の確率密度関数の描画
plot_std_normal(lower, upper, ax=ax)
# 長方形の描画
r = patches.Rectangle(xy=(-4, 0), width=8, height=0.4, ec='tab:red', fill=False)
ax.add_patch(r);【実行結果】

長方形めがけて一様分布乱数を当て込むイメージを描画します。
### 81ページ 一様分布乱数の生成
## 乱数生成
# 生成する乱数の個数
iter = 20
# 乱数生成器の設定
rng = np.random.default_rng(seed=123)
# プロットする乱数のX軸上の座標
dots_x = rng.uniform(size=iter, low=-4, high=4)
# プロットする乱数のY軸上の座標
dots_y = rng.uniform(size=iter, low=0, high=0.4)
## 描画処理
# 描画領域の設定
fig, ax = plt.subplots(figsize=(6, 3))
# 標準正規分布の確率密度関数の描画
plot_std_normal(lower, upper, ax=ax)
# 長方形の描画
r = patches.Rectangle(xy=(-4, 0), width=8, height=0.4, ec='tab:red', fill=False)
ax.add_patch(r)
# 乱数の散布図の描画
plt.scatter(dots_x, dots_y, s=80, color='tomato', ec='white', alpha=0.5);【実行結果】
20個の乱数を当て込んで、青塗り部分にあたったのは4個です。

本番開始です!
50万個の乱数を生成して、青塗りに当たった割合を算出します。
### 82ページ 一様分布乱数の生成 50万個
## 乱数生成
# 生成する乱数の個数
iter = 500000
# 乱数生成器の設定
rng = np.random.default_rng(seed=123)
# 座標情報の形式で乱数を生成し、データフレーム化
dots = pd.DataFrame(dict(x=rng.uniform(size=iter, low=-4, high=4),
y=rng.uniform(size=iter, low=0, high=0.4)))
## 青塗りの領域内に落ちた乱数を数える
inner = dots[(dots['x'] > -1.96) & (dots['x'] < 1.96)
& (dots['y'] < stats.norm.pdf(x=dots['x'], loc=0, scale=1))
].shape[0]
inner / iter # 全乱数のうち、青色の領域内に落ちた乱数の割合 【実行結果】

長方形の面積は横$${8}$$$${\times}$$縦$${0.4=3.2}$$であり、この面積のうち、0.2969844 の割合が青塗り部分の面積となります。
### 82ページ 面積の計算
8 * 0.4 * 0.297808【実行結果】
約95%になりました!すごい!!

今回の写経は以上です。
シリーズの記事
次の記事
前の記事
目次
ブログの紹介
note で7つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
Python、EXCELのサンプルコードの配布もあります。
2.実験!たのしいベイズモデリング1&2をPyMC Ver.5で
書籍「たのしいベイズモデリング」・「たのしいベイズモデリング2」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは R言語+Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう!
3.実験!岩波データサイエンス1のベイズモデリングをPyMC Ver.5で
書籍「実験!岩波データサイエンスvol.1」の4人のベイジアンによるベイズモデルを PyMC Ver.5で描いて分析します。
この書籍はベイズプログラミングのイロハをざっくりと学ぶことができる良書です。
楽しくPyMCモデルを動かして、ベイズと仲良しになれた気がします。
みなさんもぜひぜひPyMCで動かして、一緒に遊んで学びましょう!
4.楽しい写経 ベイズ・Python等
ベイズ、Python、その他の「書籍の写経活動」の成果をブログにします。
主にPythonへの翻訳に取り組んでいます。
写経に取り組むお仲間さんのサンプルコードになれば幸いです🍀
5.RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析をPythonとPyMC Ver.5 で実践します。
この書籍には時系列分析のテーマが盛りだくさん!
時系列分析の懐の深さを実感いたしました。
大好きなPythonで楽しく時系列分析を学びます。
6.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
統計・データサイエンス書籍にまつわる記事が多いです。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
7.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。
最後までお読みいただきまして、ありがとうございました。
