
「数値シミュレーションで読み解く統計のしくみ」をPythonで写経 ~ 第7章7.4「発展的な課題」回帰分析と自己相関・階層性
第7章「回帰分析とシミュレーション」
書籍の著者 小杉考司 先生、紀ノ定保礼 先生、清水裕士 先生
この記事は、テキスト「数値シミュレーションで読み解く統計のしくみ」第7章「回帰分析とシミュレーション」の7.4節「発展的な課題」、7.6節「演習問題」の Python写経活動 を取り扱います。
第7章は回帰分析を掘り下げます。
今回はデータに自己相関・階層性がある場合の回帰分析の問題と対処法を実践します。

R の基本的なプログラム記法はざっくり Python の記法と近いです。
コードの文字の細部をなぞって、R と Python の両方に接近してみましょう!
ではテキストを開いてシミュレーションの旅に出発です🚀
はじめに
テキスト「数値シミュレーションで読み解く統計のしくみ」のご紹介
このシリーズは書籍「数値シミュレーションで読み解く統計のしくみ〜Rでためしてわかる心理統計」(技術評論社、「テキスト」と呼びます)の Python写経です。
テキストは、2023年9月に発売され、副題「Rでためしてわかる心理統計」のとおり、統計処理に定評のある R の具体的なコードを用いて、心理統計の理解に役立つ数値シミュレーションを実践する素晴らしい書籍です。
引用表記
この記事は、出典に記載の書籍に掲載された文章及びコードを引用し、適宜、掲載文章とコードを改変して書いています。
【出典】
「数値シミュレーションで読み解く統計のしくみ〜Rでためしてわかる心理統計」初版第1刷、著者 小杉考司・紀ノ定保礼・清水裕士、技術評論社
記事中のイラストは、「かわいいフリー素材集いらすとや」さんのイラストをお借りしています。
ありがとうございます!
7.4 発展的な課題
この章では以下の2つのデータを取り扱います
① 自己相関を持ったデータ
② 階層性を持ったデータ

この記事は Jupyter Notebook 形式(拡張子 .ipynb)でPythonコードを書きます。
概ね確率分布の特性値算出には scipy.stats を用い、乱数生成には numpy.random.generator を用いるようにしています。
主に利用するライブラリをインポートします。
### インポート
# 数値計算
import numpy as np
# データフレーム
import pandas as pd
# 確率・統計
import statsmodels.api as sm # 回帰分析等の統計処理
import statsmodels.formula.api as smf # 回帰分析等の統計処理
# 線形代数
from scipy.linalg import toeplitz # 自己相関を仮定した回帰モデルで使用
# グラフ描画
from graphviz import Digraph
# 描画
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams.update(plt.rcParamsDefault)
plt.rcParams['font.family'] = 'Meiryo'
7.4.1 自己相関を持ったデータ
■ 回帰分析の仮定の1つ
テキストによると「回帰分析は仮定としてデータの独立性を求めており」、各データの「誤差間に相関が無いこと」を仮定しています。
■ 自己相関
時系列的なデータには観測時点間に相関があります。
この相関を自己相関と呼びます。
テキストの数式をお借りして、誤差に自己相関を含むモデル=自己回帰モデルを定義します。
時点$${t}$$の誤差$${E_t}$$が1時点前の誤差$${E_{t-1}}$$に$${\alpha}$$を乗じた影響を受ける感じです。
$$
E_t \sim \alpha E_{t-1} + \text{Normal}\ (0,\ \sigma)
$$

■ $${n}$$個の自己相関を持つ誤差データを作る
テキスト289ページの自己相関を持つ誤差データを作るコードを書きます。
サンプルサイズ$${n=100}$$、影響力$${\alpha=0.3}$$です。
### 289ページ n個の自己相関を持つ誤差を生成する
## 設定と準備
n = 100 # サンプルサイズ
alpha = 0.3 # 自己相関係数
## 正規分布ノイズの作成
rng = np.random.default_rng(seed=0)
e_tmp = rng.standard_normal(size=n)
## 誤差eの作成
e = np.zeros(n)
e[0] = e_tmp[0]
for t in range(1, n):
e[t] = alpha * e[t-1] + e_tmp[t]誤差データの時系列折れ線グラフを描画します。
### 誤差eの描画
plt.plot(e, '-o', lw=1, ms=3);【実行結果】


■ 自己相関がないデータと自己相関があるデータを比べる
回帰モデル$${Y_t = \beta_0 + \beta_1 x_1 + E}$$で2つのデータを生成し、散布図で比較します。
自己相関がないデータでは誤差を標準正規分布乱数とし、自己相関があるデータでは上記の誤差データを用います。
### 289~290ページ 自己相関のあるデータ、自己相関のないデータの散布図
# 図7.13, 図.14
## 設定と準備
beta0 = 1 # 回帰係数1 切片
beta1 = 2 # 回帰係数2 傾き
acs = 0.9 # 自己相関係数
n = 200 # サンプルサイズ
## データの生成
rng = np.random.default_rng(seed=0)
# x: 範囲[-1, 1)の連続一様分布乱数
x = rng.uniform(size=n, low=-1, high=1)
# ノイズ: 標準正規分布乱数
e_tmp = rng.standard_normal(size=n)
# 誤差e: 自己相関あり
e = np.zeros(n)
e[0] = e_tmp[0]
for t in range(1, n):
e[t] = acs * e[t-1] + e_tmp[t]
# 自己相関のないy
y_plane = beta0 + beta1 * x + e_tmp
# 自己相関のあるy
y_time = beta0 + beta1 * x + e
## 自己相関がないデータの散布図
# 描画領域の設定
plt.figure(figsize=(6, 3))
# 散布図の描画
plt.scatter(x, y_plane, s=50, ec='white')
# x軸ラベル、y軸ラベル、タイトルの設定
plt.xlabel('x')
plt.ylabel('y')
plt.title('自己相関がないデータの散布図'
f'\n相関係数:{np.corrcoef(x, y_plane)[0, 1]:.3f}')
plt.show()
## 自己相関があるデータの散布図
# 描画領域の設定
plt.figure(figsize=(6, 3))
# 散布図の描画
plt.scatter(x, y_time, s=50, ec='white')
# x軸ラベル、y軸ラベル、タイトルの設定
plt.xlabel('x')
plt.ylabel('y')
plt.title('自己相関があるデータの散布図'
f'\n相関係数:{np.corrcoef(x, y_time)[0, 1]:.3f}')
plt.show()【実行結果】
テキストの記載どおり、散布図を見るだけで時系列データかどうかを見抜くことは難しいことが分かりました。



■ 自己相関の有無の確認
自己相関を可視化して自己相関の有無を確認します。
statsmodels の plot_acf 関数でコレログラムを描画します。
こちらは自己相関のないデータのコレログラムです。
### 290ページ 自己相関のないデータの自己相関の図 291ページ図7.15
# 描画領域の設定
fig, ax = plt.subplots(figsize=(6, 3))
# コレログラムの描画 statsmodelsを使用
sm.graphics.tsa.plot_acf(y_plane, lags=23, auto_ylims=True, ax=ax)
# x軸ラベル、y軸ラベル、タイトルの設定
ax.set(xlabel='Lag',ylabel='ACF', title='自己相関がないデータ');【実行結果】
薄い青は95%信頼区間を示しています。
自己相関がないデータのコレログラムでは、1時点隣(ラグ1)以降で相関がほとんどありません。

こちらは自己相関があるデータのコレログラムです。
### 291ページ 自己相関のあるデータの自己相関の図 図7.15
# 描画領域の設定
fig, ax = plt.subplots(figsize=(6, 3))
# コレログラムの描画 statsmodelsを使用
sm.graphics.tsa.plot_acf(y_time, lags=23, auto_ylims=True, ax=ax)
# x軸ラベル、y軸ラベル、タイトルの設定
ax.set(xlabel='Lag',ylabel='ACF', title='自己相関があるデータ');【実行結果】
自己相関があるデータのコレログラムでは、ラグ5~7くらいまで相関があります。


■ 自己相関があるデータの回帰分析を行うことの問題
自己相関があるデータの回帰分析の結果、係数の標準誤差は大きくなりがちとなる点が問題だそうです。
この問題をシミュレーションで確かめます。
テキストと同じ段階を踏んで実装します。
① データ作成関数の定義
### 292ページ 残差に自己相関があるデータ/ないデータを生成する関数
def auto_dataset(n, beta0, beta1, alpha, sigma):
## 説明変数xの作成
x = rng.uniform(size=n, low=-1, high=1)
## 自己相関のある残差をつくる
e_tmp = rng.normal(size=n, loc=0, scale=sigma)
e = np.zeros(n)
e[0] = e_tmp[0]
for t in range(2, n):
e[t] = alpha * e[t-1] + e_tmp[t]
## 自己相関のある残差がついたモデルからデータ生成
y_time = beta0 + beta1 * x + e
## 自己相関のない残差がついたモデルからデータ生成
y_plain = beta0 + beta1 * x + e_tmp
## データフレーム化
tmp = pd.DataFrame({
'x': x,
'y_time': y_time,
'y_plain': y_plain,
'time': range(1, n+1)})
return tmp② データ作成の実行と基本統計量の確認
シミュレーション回数 1000 回、サンプルサイズ$${n=200}$$、切片$${\beta_0=1}$$、傾き$${\beta_1=1.5}$$、残差標準偏差$${\sigma=1}$$、残差の自己相関係数$${\alpha=0.7}$$で実行です!
### 292ページ 残差に自己相関あり/なしデータの回帰係数の推定値・標準誤差を確認
## 設定と準備
iter = 1000 # シミュレーション回数
n = 200 # サンプルサイズ
beta0 = 1 # 切片
beta1 = 1.5 # 傾き
alpha = 0.7 # 残差の自己相関係数
sigma = 1 # 残差の標準偏差
rng = np.random.default_rng(seed=0)
# 結果を格納するオブジェクト
result = np.zeros((iter, 4))
## シミュレーション
for i in range(iter):
# データセットの作成
dataset = auto_dataset(n=n, beta0=beta0, beta1=beta1, alpha=alpha,
sigma=sigma)
# 自己相関のないデータの回帰分析
model_plain = smf.ols(formula='y_plain ~ x', data=dataset).fit()
# 自己相関のあるデータの回帰分析
model_time = smf.ols(formula='y_time ~ x', data=dataset).fit()
# 結果の格納
result[i, 0] = model_plain.params.values[0] # 自己相関なし・beta0
result[i, 1] = model_plain.params.values[1] # 自己相関なし・beta1
result[i, 2] = model_time.params.values[0] # 自己相関あり・beta0
result[i, 3] = model_time.params.values[1] # 自己相関あり・beta1
## 結果
df = pd.DataFrame(result,
columns=['beta0plain', 'beta1plain', 'beta0time', 'beta1time'])
df.describe()【実行結果】
データの基本統計量を表示しました。
左から自己相関のないデータの切片と傾き、自己相関があるデータの切片と傾きです。

テキストの記載どおり、自己相関があるデータの係数の標準偏差(std)は大きくなりがちです。
③ 係数の分布の可視化
係数の分布を可視化してバラツキの違いを確認します。
### 294ページ 図7.17 自己相関の有無と切片の推定値の分布
# 描画領域の設定
fig, ax = plt.subplots(figsize=(6, 3))
# 自己相関なしの切片の推定値のカーネル密度推定の描画
sns.kdeplot(data=df, x='beta0plain', label='自己相関なし', ax=ax)
# 自己相関なしの切片の推定値のカーネル密度推定の描画
sns.kdeplot(data=df, x='beta0time', color='tab:red', ls='--',
label='自己相関あり', ax=ax)
# 切片の理論値1の垂直線の描画
ax.axvline(1, color='black')
# x軸範囲、y軸範囲、x軸ラベル、タイトルの設定
ax.set(xlim=(0.5, 1.5), ylim=(-0.3, 10), xlabel='beta0',
title='density plot of beta0')
# 凡例表示
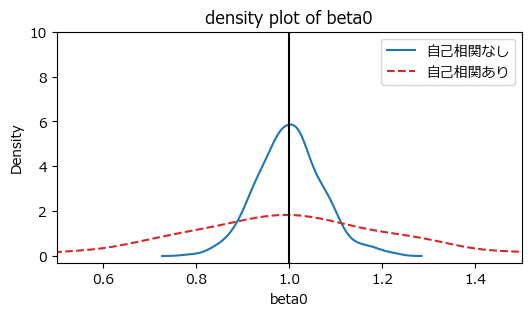
ax.legend();【実行結果】
こちらは切片の比較です。
自己相関ありのほうがバラツキ・標準偏差が大きいようです。
### 294ページ 図7.18 自己相関の有無と傾きの推定値の分布
# 描画領域の設定
fig, ax = plt.subplots(figsize=(6, 3))
# 自己相関なしの切片の推定値のカーネル密度推定の描画
sns.kdeplot(data=df, x='beta1plain', label='自己相関なし', ax=ax)
# 自己相関なしの切片の推定値のカーネル密度推定の描画
sns.kdeplot(data=df, x='beta1time', color='tab:red', ls='--',
label='自己相関あり', ax=ax)
# 切片の理論値1の垂直線の描画
ax.axvline(1.5, color='black')
# x軸範囲、y軸範囲、x軸ラベル、タイトルの設定
ax.set(xlim=(0.9, 2.1), ylim=(-0.3, 10), xlabel='beta0',
title='density plot of beta1')
# 凡例表示
ax.legend();【実行結果】
こちらは傾きの比較です。
自己相関ありのほうがバラツキ・標準偏差が大きいようです。

自己相関があるデータに普通の回帰分析を適用すると、係数の標準誤差が大きくなる(なりがち)という問題点を確認できました。

■ 自己相関を仮定した回帰モデルを他の回帰モデルと比較する
テキストは以下の3モデルについて、傾きのタイプⅠエラー確率と標準誤差を比較して、「時系列的なデータの特性を分析に反映させるモデル」を検討します。
時間変数を説明変数にしたモデル1(NG例)
時間変数を説明変数に追加した重回帰モデル2(NG例)
自己相関を仮定したモデル3(本命)
3番のモデルが本命であり、Rでは nlme パッケージの gls 関数を用いるとしています。
Python の statsmodels を使ってみます。
ただシンプルなコードを見つけることができず、statsmodels の公式サイトで例示された少々複雑なコードを使います。
自己相関を持つデータの生成と3つのモデルによる回帰分析を実行する関数を定義します。
### 295ページ 以下の3モデルのシミュレーションを行って標準誤差とp値を取得する関数
# 1. 時間変数を説明変数にしたモデル model_ill_1
# 2. 時間変数を説明変数に追加したモデル model_ill_2
# 3. 自己相関を仮定した回帰モデル model_auto
## 設定と準備
iter = 1000 # シミュレーション回数
n = 200 # サンプルサイズ
beta0 = 1 # 切片
beta1 = 0 # 傾き
alpha = 0.7 # 残差の自己相関係数
sigma = 1 # 残差の標準偏差
rng = np.random.default_rng(seed=123)
# 結果を格納するオブジェクト
result = np.zeros((iter, 6))
## シミュレーション
for i in range(iter):
# データセットの作成
dataset = auto_dataset(n=n, beta0=beta0, beta1=beta1, alpha=alpha,
sigma=sigma)
# 間違ったモデル1: 時間変数で回帰する
model_ill_1 = smf.ols(formula='y_time ~ time', data=dataset).fit()
# 間違ったモデル2: 時間変数を追加して回帰する
model_ill_2 = smf.ols(formula='y_time ~ x + time', data=dataset).fit()
# 正しく自己相関を組み込んだモデル
# Rのnlme glsの代替処理:次のサイトのols→残差のols→glsを使用
# https://www.statsmodels.org/stable/generated/statsmodels.regression.linear_model.GLS.html
ols_resid = smf.ols(formula='y_time ~ x', data=dataset).fit().resid.values
resid_fit = sm.OLS(ols_resid[1:], ols_resid[:-1]).fit()
rho = resid_fit.params
order = toeplitz(np.arange(len(dataset)))
sigma_auto = rho**order
model_auto = smf.gls(formula='y_time ~ x', sigma=sigma_auto,
data=dataset).fit()
# 結果の格納
result[i, 0] = model_ill_1.bse.values[1] # SE
result[i, 1] = model_ill_1.pvalues.values[1] # p値
result[i, 2] = model_ill_2.bse.values[1] # SE
result[i, 3] = model_ill_2.pvalues.values[1] # p値
result[i, 4] = model_auto.bse.values[1] # SE
result[i, 5] = model_auto.pvalues.values[1] # p値
## 結果(データフレームに)
df = pd.DataFrame(result,
columns=['SE_il_1', 'p_ill_1', 'SE_ill_2', 'p_ill_2',
'SE_auto', 'p_auto'])続いてタイプⅠエラー確率を算出します。
### 296ページ 続き Type I Error率を計算
df['FLG_1'] = (df['p_ill_1'] <= 0.05) * 1
df['FLG_2'] = (df['p_ill_2'] <= 0.05) * 1
df['FLG_auto'] = (df['p_auto'] <= 0.05) * 1
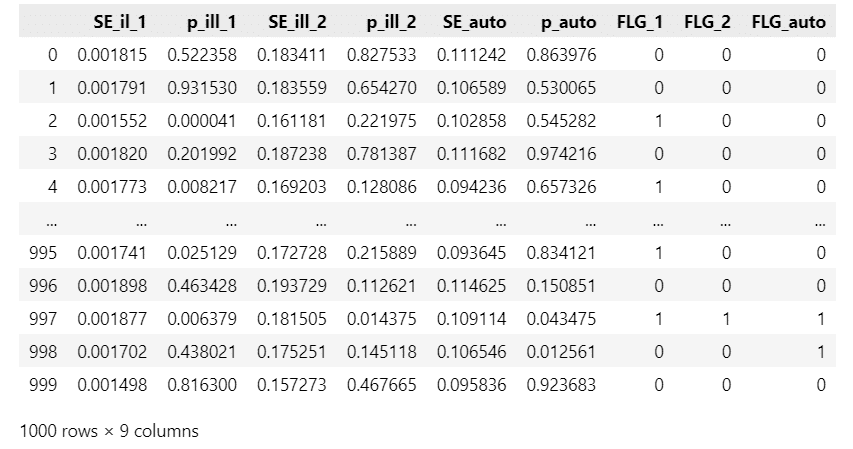
df【実行結果】
左からモデル1・2・3の傾きの標準誤差 SE と$${p}$$値、モデル1・2・3の$${p}$$値が有意水準$${5\%}$$で有意1、有意でない0のフラグです。
では各モデルの傾きのタイプⅠエラー確率と標準誤差を比較しましょう。
間違ったモデル1です。
### 296ページ 続き 間違ったモデル1のType I Error率
df['FLG_1'].mean()【実行結果】
タイプⅠエラー確率がとても大きな値になりました。
有意水準$${5\%}$$と大きく乖離しています。

### 296ページ 続き 間違ったモデル1の標準誤差
df['SE_ill_1'].mean()【実行結果】

続いて間違ったモデル2です。
### 296ページ 続き 間違ったモデル2のType I Error率
df['FLG_2'].mean()【実行結果】

### 297ページ 続き 間違ったモデル2の標準誤差
df['SE_ill_2'].mean()【実行結果】
タイプⅠエラー確率は有意水準$${5\%}$$に近くなったものの、標準誤差が大きくなっています。

最後に正しく自己相関を組み込んだモデル3です。
### 297ページ 続き 正しいモデルのタイプⅠエラー確率
df['FLG_auto'].mean()【実行結果】
タイプⅠエラー確率は有意水準$${5\%}$$を下回っています。

### 297ページ 続き 正しいモデルの標準誤差
df['SE_auto'].mean()【実行結果】
標準誤差はモデル2と比べて小さくなっています。
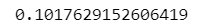
テキストの項の最後に時系列データ分析の書籍が紹介されています。
「RとStanではじめる心理学のための時系列分析入門」
時系列分析の多くのトピックを広く体感できる良書です!
私はPython寄り道写経を実践してブログ記事を書いています。
よかったらお読みくださいね🍀

7.4.2 階層性を持ったデータ
テキストの「クラスタ$${j}$$に属する個人$${i}$$」を例にして階層を持つデータのイメージ図を描いてみます。
### 階層のイメージ
# 無向グラフオブジェクトの生成 neatoでnodeの位置調整を実施
g = Graph(engine='neato')
# 基本属性の設定
g.attr('node', shape='box', fontname='Meiryo UI')
g.graph_attr['rankdir'] ='LR'
# 頂点の作成、位置posを設定
for j in range(4):
g.node(f'クラスタ{j}', pos=f'{j*3 + 1}, 1!')
for i in range(12):
g.node(f'個人{i}', pos=f'{i}, 0!')
# 辺の作成
for k in range(12):
g.edge(f'クラスタ{k//3}', f'個人{k}')
# グラフの描画
g【実行結果】

テキストは、階層データは各クラスタの中で誤差が相関していると考えられる、とし、クラスタ$${j}$$に属する個人$${i}$$の反応$${y_{ij}}$$が説明変数$${x_{ij}}$$から影響されているケースの線形モデルを定式化しています。
以下、テキストの数式をお借りします。
$$
\begin{align*}
Y_{ij} &= \beta_{0j} + \beta_{1j} x_{ij} + E_{ij} \\
\beta_{0j} &= \gamma_{00} + \gamma_{10} z + U_{00} \\
\beta_{1j} &= \gamma_{01} + \gamma_{11} w + U_{11} \\
\\
\beta_{0j} &\sim \text{Normal}\ (\gamma_{00},\ \tau_{00}) \\
\beta_{1j} &\sim \text{Normal}\ (\gamma_{01},\ \tau_{11}) \\
\\
\boldsymbol{\beta} &\sim \text{MultivariateNormal}\ (\gamma,\ \tau) \\
\gamma &= [\gamma_{00},\ \gamma_{01}] \\
\tau &= [[\tau_{00}^2,\ \tau_{00} \tau_{11} \rho], [\tau_{00} \tau_{11} \rho,\ \tau_{11}^2]] \\
\end{align*}
$$
$${\rho}$$は上位レベルの係数間の相関係数です。
シミュレーションでは$${\boldsymbol{\beta} \sim \text{MultivariateNormal}\ (\gamma,\ \tau)}$$を用いてデータ生成します。

■ 多変量正規分布乱数の罠
テキストは多変量正規分布で乱数生成する際に、引数「empirical=TRUE」を指定しています。
生成されたデータの平均・分散・共分散が、指定した「平均ベクトル」と「分散共分散行列」とピッタリ一致するように作成するオプションです。
Pythonの多変量正規分布乱数生成ライブラリで「empirical=TRUE」と同等の出力ができるものを探しましたが、見つけることができませんでした…
そこで、Python で R の mvnorm() を動かして「empirical=TRUE」の多変量正規分布乱数を取得することにします!

■ Python で R を動かす練習
pyper ライブラリを使って Python から R を動かします。
準備します。
変数 rcmd にはご自身の R のパスを指定してください。
また、R の環境に MASS パッケージをインストールしておいてください。
### 追加インポートと環境設定
import pyper
rcmd = r"xxxxxxxx\R-4.3.3\bin\R.exe" # ← Rのパスを指定練習します。
テキスト299ページのデータ生成と同じロジックで作成したテストコードを実行します。
### テスト
## Rのインスタンスを作成してMASSパッケージを読み込む
r = pyper.R(RCMD=rcmd, use_pandas='True', use_numpy='True')
r('library(MASS)')
## パラメータ設定(Python側)
nc=4
n=3
beta0_mu=0.5
beta1_mu=2.5
beta0_sd=3
beta1_sd=5
rho=0.5
## データ作成(Python側)
# 総数はクラスタ数ncにクラスタ内データ数をかけたもの
n_all = nc * n
c_level = np.repeat(a=range(1, nc+1), repeats=n) # クラスタ番号を格納
# 説明変数
rng = np.random.default_rng(seed=123)
x = rng.uniform(size=n_all, low=-10, high=10)
# 平均ベクトル
MU = np.array([beta0_mu, beta1_mu])
# 誤差の分散共分散行列
SIGMA = np.array([[beta0_sd**2, beta0_sd * beta1_sd * rho],
[beta0_sd * beta1_sd * rho, beta1_sd**2]])
## Rで多変量正規分布乱数を作成してPythonで受け取る処理
# Pythonの変数nc, MU, SIGMAの値をRへ渡す
r.assign("nc", nc)
r.assign("MU", MU)
r.assign("SIGMA", SIGMA)
# Rでmvrnormを実行
r("Beta <- mvrnorm(nc, MU, SIGMA, empirical=T)")
# Rの変数Betaの値をPythonで受け取る
r.get("Beta")【実行結果】
4つのクラスタの切片と傾きの値をPython側で取得・表示できました!


■ 本番実装とテスト
テキストの階層データ作成関数を定義して、テスト実行します
まずは関数定義から。
### 299ページ 多変量正規分布乱数生成をRで実行して階層データのサンプルを作る関数
def HLM_datasetR(nc, n, beta0_mu, beta1_mu, beta0_sd, beta1_sd, rho, sigma):
## 総数はクラスタ数ncにクラスタ内データ数をかけたもの
n_all = nc * n
c_level = np.repeat(a=range(1, nc+1), repeats=n) # クラスタ番号を格納
## データの生成
# 説明変数
x = rng.uniform(size=n_all, low=-10, high=10)
# 平均ベクトル
MU = np.array([beta0_mu, beta1_mu])
# 誤差の分散共分散行列
SIGMA = np.array([[beta0_sd**2, beta0_sd * beta1_sd * rho],
[beta0_sd * beta1_sd * rho, beta1_sd**2]])
## RとPythonでやり取りして多変量正規分布乱数を生成 ※empirical対応!
# pythonからRへ変数(mvrnormのパラメータ値)を渡す
r.assign("nc", nc)
r.assign("MU", MU)
r.assign("SIGMA", SIGMA)
# ★★Rで多変量正規分布乱数を生成する empirical=TRUEです!★★
r("Beta <- mvrnorm(nc, MU, SIGMA, empirical=T)")
# Rの変数BetaをPythonで受け取る(get)
Beta = r.get("Beta")
## クラスタごとに係数を割り当て
beta0 = np.repeat(a=Beta[:, 0], repeats=n)
beta1 = np.repeat(a=Beta[:, 1], repeats=n)
# 下位レベルでの誤差生成
err = rng.normal(size=n_all, loc=0, scale=sigma)
# 目的変数を生成
y = beta0 + beta1 * x + err
## データセットに組み上げる ※クラスタ列名はgroupに変更(classはpython予約語)
dataset = pd.DataFrame(
dict(x=x, group=c_level, beta0=beta0, beta1=beta1, y=y))
return dataset関数の動作確認をします。
説明変数$${x}$$、クラスタ、クラスタ別の係数$${\beta_0,\ \beta_1}$$、目的変数$${y}$$を生成します。
クラスタの数$${nc=4}$$、各クラスタのサンプルサイズ$${n=3}$$、係数$${\beta_0,\beta_1}$$の平均値$${0.5,\ 2.5}$$・標準偏差$${3,\ 5}$$、残差標準誤差$${\sigma=1}$$、相関係数$${\rho=0.5}$$をパラメータ設定しています。
### 300ページ サンプル作成のテスト
# Rのインスタンスを作成してMASSパッケージを読み込む
r = pyper.R(RCMD=rcmd, use_pandas='True', use_numpy='True')
r("library(MASS)")
# サンプルデータを作成する
HLM_datasetR(nc=4, n=3, beta0_mu=0.5, beta1_mu=2.5, beta0_sd=3, beta1_sd=5,
rho=0.5, sigma=1)【実行結果】
テキストのクラスタの変数名 class は Python 予約語と重なるため、変数名を group に変更しました。

階層レベルを考慮したモデルで係数等を推定してみます。
statsmodels の mixedlm (混合線形モデル)を利用します。
### 301ページ 階層モデルの動作確認1 固定効果 β0, β1
# Rのインスタンスを作成してMASSパッケージを読み込む
r = pyper.R(RCMD=rcmd, use_pandas='True', use_numpy='True')
r("library(MASS)")
## データセットを取得
rng = np.random.default_rng(seed=3)
dataset = HLM_datasetR(nc=20, n=200,
beta0_mu=0.5, beta1_mu=2.5,
beta0_sd=3, beta1_sd=5,
rho=0.5, sigma=1)
# 一般化線形混合モデル by statsmodels
# y ~ 1 + x + (1 + x | group) 相当(のはず)
model_mlm = smf.mixedlm('y ~ x', data=dataset, groups=dataset['group'],
re_formula='x')
result_mlm = model_mlm.fit()
print(result_mlm.summary())【実行結果】

係数の推定値はパラメータ設定した値に近似しました。
・$${\beta_0=0.5}$$・・・Intercept の Coef. $${0.500}$$と一致
・$${\beta_1=2.5}$$・・・x の Coef. $${2.506}$$とほぼ一致
その他のパラメータ設定値を確認します。
係数の変量効果の分散共分散行列を表示します。
### β0jとβ1jの変量効果の分散共分散行列
result_mlm.cov_re【実行結果】
この分散共分散行列を用いて、パラメータ設定値と比較します!

係数の変量効果の標準誤差です。
### 301ページ 階層モデルの動作確認2 β0jとβ1jの変量効果の標準偏差
interept_std, x_std = np.diag(result_mlm.cov_re**0.5)
pd.DataFrame(
[interept_std, x_std], index=['Intercept', 'x'], columns=['Std.Dev.']
).round(3)【実行結果】

係数の変量効果の標準誤差はパラメータ設定した値に近似しました。
・$${\beta_0}$$の標準誤差$${3}$$・・・Intercept の Std.Dev. $${3.000}$$と一致
・$${\beta_1}$$の標準誤差$${5}$$・・・x の Std.Dev. $${5.005}$$とほぼ一致
係数の変量効果の相関係数です。
### 301ページ 階層モデルの動作確認3 β0jとβ1jの変量効果の相関係数
round(result_mlm.cov_re.iloc[0, 1] / interept_std / x_std, 3)【実行結果】

係数の変量効果の相関係数はパラメータ設定した値に近似しました。
・$${\rho=0.5}$$・・・$${0.501}$$とほぼ一致
ではシミュレーション本番に突入です!

■ 階層データの回帰分析の比較
普通の線形回帰モデル(OLS)と混合線形モデルの分析結果を比較します。
シミュレーション回数は 1000 回です。
### 301ページ 階層モデルと普通の回帰モデルの推定精度の違いをシミュレーション
# シミュレーション回数1000回:15分
## 設定と準備
iter = 1000 # シミュレーション回数
seed = 123 # 乱数シード
## 結果を格納するオブジェクト
result = np.zeros((iter, 4))
## Rのインスタンスを作成してMASSパッケージを読み込む
r = pyper.R(RCMD=rcmd, use_pandas='True', use_numpy='True')
r("library(MASS)")
## Rの乱数シードを設定する
r.assign("seed", seed)
r("set.seed=seed")
## シミュレーション
rng = np.random.default_rng(seed=123)
for i in range(iter):
## データセットをつくる
dataset = HLM_datasetR(nc=20, n=200, beta0_mu=0.5, beta1_mu=2.5,
beta0_sd=3, beta1_sd=5, rho=0.5, sigma=1)
## 普通の回帰分析
model_ols = smf.ols(formula='y ~ x', data=dataset).fit()
## 階層モデル
model_lme = smf.mixedlm('y ~ x', data=dataset, groups=dataset['group'],
re_formula='x').fit()
## 結果の格納
result[i, 0] = model_ols.params.values[0] # 普通モデル切片
result[i, 1] = model_lme.params.values[0] # 階層モデル切片
result[i, 2] = model_ols.params.values[1] # 普通モデル傾き
result[i, 3] = model_lme.params.values[1] # 階層モデル傾き
## 結果(データフレームに)
df = pd.DataFrame(result,
columns=['beta0_OLS', 'beta0_HLM', 'beta1_OLS', 'beta1_HLM'])
display(df.describe())【実行結果】
テキストのとおり、普通の回帰分析の結果、「切片や傾きの平均」は「平均的にはうまくいっているようですが、標準誤差が大きくなっています」。
階層モデルを表現できる混合線形モデルの方が、標準誤差(バラツキ)が小さく、「安定して正しい推定値を得ていることがわかります」。

2つのモデルの2つの係数のサンプルデータを可視化します。
### 303ページ 図7.19 階層データの切片の推定値の分布
# 描画領域の設定
fig, ax = plt.subplots(figsize=(6, 3))
# HLMの切片の推定値のカーネル密度推定の描画
sns.kdeplot(data=df, x='beta0_HLM', label='HLM', ax=ax)
# OLSの切片の推定値のカーネル密度推定の描画
sns.kdeplot(data=df, x='beta0_OLS', color='tab:red', ls='--', label='OLS', ax=ax)
# 切片の理論値0.5の垂直線の描画
ax.axvline(0.5, color='black')
# x軸範囲、y軸範囲、x軸ラベル、タイトルの設定
ax.set(xlim=(-0.1, 1.1), ylim=(-0.3, 30), xlabel='beta0',
title='density plot of beta0')
# 凡例表示
ax.legend();【実行結果】
切片の可視化です。

### 303ページ 図7.20 階層データの傾きの推定値の分布
# 描画領域の設定
fig, ax = plt.subplots(figsize=(6, 3))
# HLMの傾きの推定値のカーネル密度推定の描画
sns.kdeplot(data=df, x='beta1_HLM', label='HLM', ax=ax)
# OLSの傾きの推定値のカーネル密度推定の描画
sns.kdeplot(data=df, x='beta1_OLS', color='tab:red', ls='--', label='OLS', ax=ax)
# 傾きの理論値2.5の垂直線の描画
ax.axvline(2.5, color='black')
# x軸範囲、y軸範囲、x軸ラベル、タイトルの設定
ax.set(xlim=(2.2, 2.8), ylim=(-0.3, 200), xlabel='beta1',
title='density plot of beta1')
# 凡例表示
ax.legend();【実行結果】
傾きの可視化です。

切片も傾きも普通の回帰分析(OLS)のバラツキ(標準誤差)が大きくなっている様子が良く分かります。
テキストの言葉をお借りして締めくくります。
標準誤差が大きいということは、母数の点推定値としての信頼性が低いことを意味します。(途中省略)
また標準誤差に基づいて統計的に優位かどうかの判定をしますから、標準誤差が大きいことは判断が謝る可能性が高いことを意味します。

7.6 演習問題
実験データの分析に関する相談を受けた、というシチュエーションで4つの演習問題を解きます。
0から10の値を離散値をとる目的変数、-4 から 4 までの実数値をとる説明変数、サンプルサイズ 20、の条件で、R の lm関数(普通の回帰分析)が適するかの検討です。
7.6.1 演習問題 1
パス(目的変数が正値の離散値なことを織り込めるモデルが必要そう…)
7.6.2 演習問題 2
ポアソン分布乱数を生成してヒストグラムを描画します。
### 7.6.2 演習問題2
# 任意の期待値を設定したポアソン分布乱数を生成してヒストグラムを描画
## 設定と準備
lambda_ = 10 # ポアソン分布の期待値λ
n = 1000 # サンプルサイズ
## ポアソン分布からの乱数を生成
rng = np.random.default_rng(seed=123)
random_numbers = rng.poisson(size=n, lam=lambda_)
## ヒストグラムの描画
sns.histplot(random_numbers, bins=20, stat='frequency', kde=True, ec='white')
plt.xlabel('ポアソン分布乱数')
plt.title('Histogram of Random numbers of Poisson distribution');【実行結果】


7.6.3 演習問題 3
ポアソン分布のパラメータ$${\lambda}$$が正値をとるように指数関数で変換し、データを生成します。
### 7.6.3 演習問題3
# 指数関数exp(β0 + β1x)をポアソン分布のパラメータに与えてダミーデータを作成
## 設定と準備
n = 100 # サンプルサイズ
beta0 = 1 # 線形予測子の切片
beta1 = 2 # 線形予測子の切片
## データの作成
rng = np.random.default_rng(seed=123)
# 線形予測子の説明変数x:正規分布乱数
x = rng.standard_normal(size=n)
# ポアソン分布のパラメータλの作成:線形予測子を指数関数expで変換
lambda_ = np.exp(beta0 + beta1 * x)
# 目的変数y:λをパラメータとするポアソン分布乱数
y = rng.poisson(size=n, lam=lambda_)
## データフレームを作成
data = pd.DataFrame(dict(y=y, x=x))
# データの概要表示:形状と先頭5行
print('data.shape:', data.shape)
display(data.head())【実行結果】


7.6.4 演習問題 4
パラメータリカバリに必要なサンプルサイズの目安をシミュレーションします。
モデルには statsmodels のポアソン回帰 smf.poisson を使いました。
### 7.6.4 演習問題4
# 母数β0=1, β1=0.5の場合で、パラメータリカバリに必要なサンプルサイズの目安を
# シミュレーション
## 設定と準備
sample_sizes = [20, 50, 100, 200, 500, 1000] # サンプルサイズのパターン
true_beta0 = 1 # β0の真値
true_beta1 = 0.5 # β1の真値
num_simulations = 1000 # シミュレーション回数
rng = np.random.default_rng(seed=2) # 乱数生成器・乱数シード
## シミュレーション 各サンプルサイズでシミュレーションを行う
for n in sample_sizes:
## 結果を格納するオブジェクト
beta0_estimats = np.zeros(num_simulations)
beta1_estimats = np.zeros(num_simulations)
# シミュレーションの実行
for i in range(num_simulations):
# 説明変数xを標準正規分布からランダムに生成(実数値)
# データが標準化されている
x = rng.standard_normal(size=n)
# λを計算(指数関数で正の値に変換)
lambda_ = np.exp(true_beta0 + true_beta1 * x)
# λをパラメータとするポアソン分布から目的変数yを生成(整数値のみ)
y = rng.poisson(size=n, lam=lambda_)
# データフレームを作成
data = pd.DataFrame(dict(y=y, x=x))
# モデルを推定
model = smf.poisson(formula='y ~ x', data=data).fit(disp=False)
# パラメータの推定値を保存
beta0_estimats[i] = model.params.values[0] # 切片の推定値
beta1_estimats[i] = model.params.values[1] # 傾きの推定値
## 推定値の平均と標準偏差を表示
print('Sample size:', n)
print(f'Estimate beta0: Mean = {beta0_estimats.mean():.7f}, '
f'SE = {beta0_estimats.std(ddof=1):.7f}')
print(f'Estimate beta1: Mean = {beta1_estimats.mean():.7f}, '
f'SE = {beta1_estimats.std(ddof=1):.7f}', '\n')【実行結果】
相談時のサンプルサイズ$${n=20}$$のとき、係数の標準誤差は大きい感じです…
もう少しサンプルサイズを大きくする必要がありそうな気がするものの、標準誤差の目安が分からないです…

今回の写経は以上です。

テキストは第7章が最後の章です。
この記事がシリーズ最終回となります。
シリーズ記事を最後までお読みいただきまして、ありがとうございました!
温かく見守ってくださいました書籍著者の先生、ありがとうございました!

シリーズの記事
次の記事

前の記事
目次
ブログの紹介
note で7つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
Python、EXCELのサンプルコードの配布もあります。
2.実験!たのしいベイズモデリング1&2をPyMC Ver.5で
書籍「たのしいベイズモデリング」・「たのしいベイズモデリング2」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは R言語+Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう!
3.実験!岩波データサイエンス1のベイズモデリングをPyMC Ver.5で
書籍「実験!岩波データサイエンスvol.1」の4人のベイジアンによるベイズモデルを PyMC Ver.5で描いて分析します。
この書籍はベイズプログラミングのイロハをざっくりと学ぶことができる良書です。
楽しくPyMCモデルを動かして、ベイズと仲良しになれた気がします。
みなさんもぜひぜひPyMCで動かして、一緒に遊んで学びましょう!
4.楽しい写経 ベイズ・Python等
ベイズ、Python、その他の「書籍の写経活動」の成果をブログにします。
主にPythonへの翻訳に取り組んでいます。
写経に取り組むお仲間さんのサンプルコードになれば幸いです🍀
5.RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析をPythonとPyMC Ver.5 で実践します。
この書籍には時系列分析のテーマが盛りだくさん!
時系列分析の懐の深さを実感いたしました。
大好きなPythonで楽しく時系列分析を学びます。
6.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
統計・データサイエンス書籍にまつわる記事が多いです。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
7.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。
最後までお読みいただきまして、ありがとうございました。
