
【特集】線形単回帰モデル 第1部 概要
特集
この特集記事は、統計検定2級の出題内容に沿って、最小二乗法で推定する線形単回帰モデルの概略をまとめるものです。
この記事は2部構成の前編です。
【2つの記事】
第1部:概要(★この記事)
数式、計算を通じて統計検定2級レベルの線形単回帰分析を学びます。
第2部:ツールの活用
EXCEL、R、Pythonを用いて線形単回帰分析を実践します。
第2部のリンクはこちら。
この記事は、統計検定2級公式テキストに沿って、単回帰分析の主要なトピックスをまとめています。
回帰分析に関わる数式・公式を整理しつつ、「コーヒーデータ」を用いた図表を多用して気づきや理解を促進を目指し、さらに、Pythonを電卓代わりにして計算を実践します。
また、数式・公式が「統計ソフトウェアの出力結果」に繋がるように、関連性を整理します。
参考書籍
この記事は統計検定2級公式テキスト、および、統計検定2級公式問題集CBT対応版に準拠して書きました。
📕公式テキスト:1.6.4 回帰直線(32ページ~)、5.1.1 線形単回帰モデル(163ページ~)など
📘公式問題集
利用データ
統計検定2級公式問題集CBT対応版の問題10-1-1の「コーヒーデータ」を利用します。
問題集では1991~2015年を対象にしていますが、この記事では期間を延長して1991~2019年までを対象にします。
次のリンクはデータ入手元の「国際コーヒー機関」の統計データページです。
【出典記載】
「Total production - Crop Year : 1990- Present」
「Retail Prices - Annual Averages : 1990- Present」
(両データともに、国際コーヒー機関 International Coffee Organization)
(http://www.ico.org/new_historical.asp)
【コンテンツ編集・加工の記載】
記事の記載にあたっては、出典記載の資料を加工して作成しています。

【コーヒーデータの概要】
コーヒーデータは次の2つの量的変数で構成されています。
■ 項目「日本小売価格」
1991年から2019年までの29年間の日本の年平均小売価格(単位:米ドル/ポンド)
■ 項目「世界総生産量」
1990/91年から2018/19年(Crop year)までの29年間の世界年間総生産量(単位:100万袋)

時系列の折れ線グラフで可視化します。

CSVファイルのダウンロード
こちらのリンクからコーヒーデータのCSVファイルをダウンロードできます。
電卓代わりのPythonサンプルファイルのダウンロード
記事の途中で計算を行う際、電卓代わりにPythonを用います。
こちらのリンクからJupyter Notebook形式のサンプルファイルをダウンロードできます。
1. 回帰式
(1) 2変数の関係性
コーヒーの世界総生産量と日本小売価格の散布図を見てみましょう。

世界総生産量が増加すると日本小売価格が減少する関係がありそうです。
相関係数を確認しましょう。

相関係数は$${-0.8128}$$です。
強めの負の相関があります。
世界総生産量と日本小売価格の間に直線的な比例関係があるとするならば、どのような直線を描けるでしょうか?
(2) 回帰直線
ひとまず直線を引いてみましょう。

青いデータ点の間をバランスよく(程よく)赤い直線が突き抜けています。
相関係数が負の値であったように、直線の傾きも負の値のようです。
この直線を回帰直線と呼びます。
回帰直線を数式にしてみましょう。
$$
日本小売価格=切片+傾き\times世界総生産量
\tag{1}
$$
もう少し数式を一般化してみましょう。
日本小売価格を$${y}$$、世界総生産量を$${x}$$とします。
$$
y = \alpha + \beta x
\tag{2}
$$
式2のように回帰直線を数式化したものを回帰式と呼びます。
説明変数が1つ(単)を扱うので、単回帰式です。
回帰式に現れる変数・パラメータは次のとおりです。
$${y}$$:目的変数(応答変数、従属変数、被説明変数など)
$${x}$$:説明変数(独立変数、予測変数、など)
$${\alpha}$$:切片
$${\beta}$$:傾き
パラメータ$${\alpha, \beta}$$を回帰係数と呼びます。
(説明変数のパラメータ$${\beta}$$だけを回帰係数と呼ぶこともあります。)
コーヒーデータの例では、「世界総生産量」が説明変数となり、目的変数「日本小売価格」を説明しています。
切片と傾きの値をPythonを使って調べてみましょう。
### scipy.statsの線形単回帰
# 単回帰分析の実行
result_stats = stats.linregress(data['世界総生産量'], data['日本小売価格'])
# 予測値の計算 ※後々の計算に利用
y_pred_stats = result_stats.intercept + result_stats.slope * data['世界総生産量']
### 切片と傾きの表示
print(f'切片:{result_stats.intercept:.4f}, 傾き:{result_stats.slope:.4f}')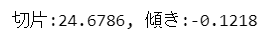
切片は$${24.6786}$$、傾きは$${-0.1218}$$です。
式2に切片と傾きを代入して、コーヒーのモデルを完成させましょう。
$$
y = 24.6786 - 0.1218 x
\tag{3}
$$
世界総生産量が1増える(100万袋増える)と日本小売価格が 0.1218 減る(1ポンドあたり0.1218米ドル減る)関係が見えました。
(3) 予測
回帰式を用いて予測してみましょう。
世界総生産量が$${100}$$(単位:100万袋)のときを考えます。
式3:回帰式の$${x}$$に$${100}$$を当てはめて、日本小売価格(単位:1ポンド当たり米ドル)$${y}$$を予測します。
$$
y = 24.6786 - 0.1218 \times 100 \fallingdotseq 12.50
$$
日本小売価格はおよそ$${12.5}$$米ドル/ポンドです。
単回帰で目的変数と説明変数のシンプルな関係を表現できると、予測値が増減する仕組みの理解や他者への説明もしやすくなる感じがします。
世の中を単回帰で予測できたらいいのに・・・(社会は複雑すぎます)
ところで、切片や傾きはどのように計算したらよいのでしょう?
(4) 残差
コーヒーデータを「観測データ」と呼ぶことにしましょう。
次のグラフをご覧ください。
観測データの各点から回帰直線に向けて垂直の線(赤い点線)を引きました。
この垂直の線について考えてみましょう。

最も左の観測データ点に注目します。
1996年、世界総生産量$${87.321}$$、日本小売価格$${15.24}$$の点です。
この点から下に垂線が降りています。
垂線と回帰直線の交わる点は、世界総生産量が$${87.321}$$のときの回帰直線の$${y}$$の予測値です。
この$${y}$$の予測値$${\hat{y}}$$を計算してみましょう。
(予測値には頭にハットを被せます🎩)
$$
\hat{y} = 24.6786 - 0.1218 \times 87.321 = 14.04
\tag{4}
$$
垂線は目的変数の観測値$${y=15.24}$$と予測値$${\hat{y}=14.04}$$の差$${1.2}$$を表しています。
目的変数の観測値と予測値の差を残差$${e}$$と呼びます。
グラフのアップで確認しましょう。

残差$${e}$$を数式にすると次のように表せます。
$${i}$$は観測データの順番を示す正の整数値です($${i=1, 2, \cdots, n}$$)。
残差は観測データの数$${n}$$だけ存在します!
$$
e_i = y_i - \hat{y}_i=y_i - (\alpha + \beta x_i)
\tag{5}
$$
回帰分析ではこの残差を用いてさまざまな分析を行います。
残差は説明変数$${x}$$を固定したときの目的変数$${y}$$の観測値と予測値の差です。
残差に説明変数$${x}$$の変動が含まれないことに留意しましょう。
(5) 残差平方和
観測データから回帰直線を求めるとき、各データ点の残差の合計が小さい方が、観測データにフィットしていると感じられます。
たとえば次のような観測データと回帰直線の場合、回帰直線は観測データにピッタリ一致(ジャストフィット!)しています。
この場合、残差はゼロです。

一方で、観測データ点と離れてすぎている直線はフィットしていないと言えるでしょう。
例えば次のような直線です。
残差を示す垂線がとても長いです。
残差が大きいことはフィットしていないことだ、と感じられます。

残差の取り扱いに話を移しましょう。
個々の観測データ点に対応する残差は合計すると0になってしまいます。
Pythonを電卓代わりにして残差の合計してみましょう。
### 残差の合計の計算
# yの予測値と残差の計算
resid_stats = data['日本小売価格'] - y_pred_stats
# 残差を合計
resid_sum = (resid_stats).sum()
resid_sum.round(10)
>> 出力イメージ
>> -0.0残差を合計すると0になりました。
(コンピュータ計算における小数端数処理の関係で、完全な0にはなりません)
そこで、各データ点の残差を二乗して合計した「残差平方和」を利用します。
変数と平均の差を二乗する「偏差平方和」と似た考え方です。
※変数の値とその変数の平均値の差$${y_i - \bar{y}}$$を「偏差」と呼びます。
切片と傾きの推定値$${\hat{\alpha}, \hat{\beta}}$$をパラメータに持つ残差平方和$${S(\hat{\alpha}, \hat{\beta})}$$を数式で表現しましょう。
$$
S(\hat{\alpha}, \hat{\beta})=\sum^n_{i=1}e^2_i=\sum^n_{i=1}(y_i-\hat{y}_i)^2=\sum^n_{i=i}\{ y_i-(\hat{\alpha} + \hat{\beta} x_i)\}^2
\tag{6}
$$
$${\hat{\alpha}, \hat{\beta}}$$は切片の推定値と傾きの推定値です。
$${y_i, \hat{y}_i}$$は$${i}$$番目のデータの目的変数の観測値と予測値です。
$${x_i, e_i}$$は$${i}$$番目のデータの説明変数の残差です。
$${n}$$は観測データの数(標本サイズ)です。
(6) 最小二乗法による回帰係数の算出
残差平方和を最小にするような回帰係数を求める方法が最小二乗法です。
単回帰について、最小二乗法による傾きの推定値$${\hat{\beta}}$$と切片の推定値$${\hat{\alpha}}$$の公式は次のとおりです。
この公式は大切なのでぜひ覚えましょう!

【最小二乗法による単回帰の回帰係数$${\hat{\beta}}$$の算出公式】
$$
\hat{\beta}=\cfrac{\sum^n_{i=1}(y_i-\bar{y})(x_i-\bar{x})}{\sum^n_{i=1}(x_i-\bar{x})^2}=\cfrac{T_{xy}}{T_{xx}}=\cfrac{\hat{\sigma}_{xy}}{\hat{\sigma}^2_x}=r_{xy}\cfrac{\hat{\sigma}_y}{\hat{\sigma}_x}
\tag{7}
$$
標本の考え方をベースにして書きました。
記号の意味は以下のとおりです。
・$${\bar{x}, \bar{y}}$$は$${x,y}$$の平均値
・$${T_{xy}}$$は$${x,y}$$の偏差積和$${\sum^n_{i=1}(y_i-\bar{y})(x_i-\bar{x})}$$
・$${T_{xx}}$$は$${x}$$の偏差平方和$${\sum^n_{i=1}(x_i-\bar{x})^2}$$
・$${\hat{\sigma}^2_x}$$は$${x}$$の標本不偏分散
・$${\hat{\sigma}_x, \hat{\sigma}_y}$$は$${x,y}$$の標本不偏分散の標準偏差
・$${\hat{\sigma}_{xy}}$$は$${x, y}$$の共分散
・$${r_{xy}}$$は$${x, y}$$の相関係数
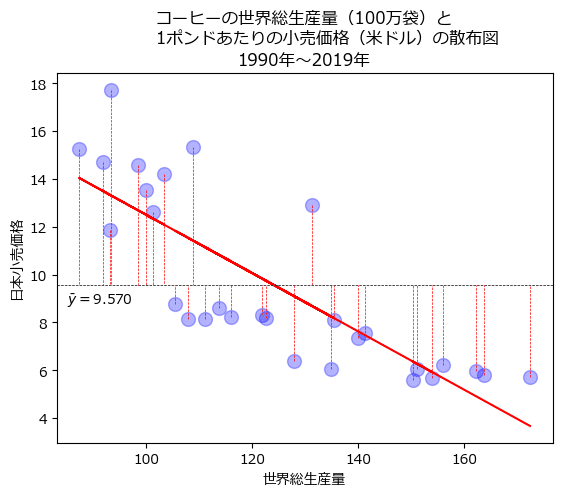
$${x}$$の偏差平方和$${T_{xx}}$$や$${x,y}$$の偏差積和$${T_{xy}}$$に現れる偏差$${x_i-\bar{x}}$$・$${y_i-\bar{y}}$$を散布図で表現しましょう。
まずは$${x}$$の偏差$${x_i-\bar{x}}$$から。
$${x}$$の平均・垂直線(黒い点線)に向かって、各観測データ点から水平線が描画されています。
この水平線の長さが$${x}$$の偏差に相当します。

続いて$${y}$$の偏差$${y_i-\bar{y}}$$。
$${y}$$の平均水平線(黒い点線)に向かって、各観測データ点から垂直線が描画されています。
この垂直線の長さが$${y}$$の偏差に相当します。
$${y}$$の偏差は残差を深掘りするときに再登場します。
【最小二乗法による単回帰の回帰係数$${\hat{\alpha}}$$の算出公式】
$$
\hat{\alpha} = \bar{y} - \hat{\beta} \bar{x}
\tag{8}
$$
コーヒーデータを使って、最小二乗法による傾きと切片を求めてみましょう。
Pythonを電卓代わりにして計算します。
① 平均値、偏差の計算
傾きと切片の計算要素である$${x, y}$$の平均値と偏差を計算します。
### 各要素の計算
x_mean = data['世界総生産量'].mean() # xの平均値
y_mean = data['日本小売価格'].mean() # yの平均値
x_dev = data['世界総生産量'] - x_mean # xの偏差
y_dev = data['日本小売価格'] - y_mean # yの偏差② $${x,y}$$の偏差積和$${T_{xy}}$$の計算
$${\hat{\beta}}$$の公式の分子である偏差積和$${T_{xy}=\sum^n_{i=1}(y_i-\bar{y})(x_i-\bar{x})}$$を計算します。
### 目的変数yと説明変数xの偏差積和の計算:xの偏差✕yの偏差の合計
T_xy = (y_dev * x_dev).sum()
T_xy
>> 出力イメージ
>> -2100.1500737931033③ $${x}$$の偏差平方和$${T_{xx}}$$の計算
$${\hat{\beta}}$$の公式の分母である偏差平方和$${T_{xx}=\sum^n_{i=1}(x_i-\bar{x})^2}$$を計算します。
### 説明変数xの偏差平方和の計算:xの偏差の二乗の合計
T_xx = (x_dev**2).sum()
T_xx
>> 出力イメージ
>> 17242.608856827588④ 傾きの推定値$${\hat{\beta}}$$の計算
$${x,y}$$の偏差積和$${T_{xy}}$$を$${x}$$の偏差平方和$${T_{xx}}$$で割ります。
小数点第4位で四捨五入しています。
### 傾きの推定値βハットの計算:xとyの偏差積和/xの偏差平方和
beta_hat = T_xy / T_xx
beta_hat.round(4)
>> 出力イメージ
>> -0.1218傾き$${\hat{\beta}}$$は$${-0.1218}$$です。
⑤ 切片の推定値$${\hat{\alpha}}$$の計算
公式に当てはめて計算します。
小数点第4位で四捨五入しています。
### 切片の推定値αハットの計算:yの平均値 - βの推定値✕xの平均値
alpha_hat = y_mean - beta_hat * x_mean
alpha_hat.round(4)
>> 出力イメージ
>> 24.6786切片$${\hat{\alpha}}$$は$${24.6786}$$です。
コーヒーデータの回帰式$${y=24.6786 -0.1218x}$$が出来上がりました。
(7) 行列を用いた最小二乗法の公式
線形代数にお詳しい方は次の行列を用いて回帰係数$${\boldsymbol{\hat{\beta}}}$$を求めてみてはいかがでしょう。
■ 最小二乗法の公式(行列編)
$${\hat{\boldsymbol{\beta}}=(X^{\top}X)^{-1}X^{\top}\boldsymbol{y}}$$
$${\hat{\boldsymbol{\beta}}}$$:回帰係数ベクトル
$${X}$$:説明変数行列
$${\boldsymbol{y}}$$:目的変数ベクトル
Pythonを電卓代わりにしてこの公式を使ってみましょう。
「np.linalg.inv(X.T @ X) @ X.T @ y」が公式に該当します。
### 最小二乗法の公式(行列編)
# 行列Xの設定:1列目は全て値1、2列目は説明変数
X = data['世界総生産量'].values
ones = np.ones(X.shape[0])
X = np.stack((ones, X), axis=-1)
print('行列Xの形状:', X.shape)
print('先頭5行\n', X[:5,:])
# ベクトルyの設定:目的変数
y = data['日本小売価格'].values
print('\nベクトルyの形状:', y.shape)
print('先頭5要素\n', y[:5])
# 最小二乗法による回帰係数の推定計算
beta_hat_mtx = np.linalg.inv(X.T @ X) @ X.T @ y
print(f'\n回帰係数\n 切片:{beta_hat_mtx[0]:.4f}, 傾き:{beta_hat_mtx[1]:.4f}')

章まとめ
1つの目的変数$${y}$$と1つの説明変数を用いて、単回帰式$${y=\alpha+\beta x}$$を組み立てます。
最小二乗法を用いて残差平方和が最小となる切片$${\alpha}$$と傾き$${\beta}$$を推定します。
最小二乗法による切片$${\alpha}$$と傾き$${\beta}$$の計算公式は次のとおりです。
$$
\begin{align*}
\hat{\beta}&=\cfrac{\sum^n_{i=1}(y_i-\bar{y})(x_i-\bar{x})}{\sum^n_{i=1}(x_i-\bar{x})^2}=\cfrac{T_{xy}}{T_{xx}}=\cfrac{\hat{\sigma}_{xy}}{\hat{\sigma}^2_x}=r_{xy}\cfrac{\hat{\sigma}_y}{\hat{\sigma}_x} \\
\\
\hat{\alpha} &= \bar{y} - \hat{\beta} \bar{x} \\
\end{align*}
$$
2. 回帰の主な性質
公式テキスト記載の「最小二乗法による回帰係数を用いる場合の回帰式の性質」について、コーヒーデータを用いて計算したり、グラフを描画して、噛み砕きます。
a~dの4つの性質は大切です。ぜひ覚えておきましょう!
この4つの性質は重回帰モデルにも当てはまります。

a.予測値$${\boldsymbol{\hat{y}_i=\hat{\alpha}+\hat{\beta}x_i}}$$の平均値は観測値$${\boldsymbol{y_i}}$$の平均値と等しい
■ 公式
$${\bar{\hat{y}} = \bar{y}}$$
Pythonを電卓代わりにして計算してみましょう。
### 基本的な性質a:予測値の平均と観測値の平均は等しい
print('予測値の平均:', y_pred_stats.mean().round(10))
print('観測値の平均:', data['日本小売価格'].mean().round(10))
目的変数の予測値の平均$${\bar{\hat{y}}}$$と観測値の平均$${\bar{y}}$$は一致しました!
b.残差$${\boldsymbol{e_i=y_i-\hat{y}}}$$の平均は0である
aの目的変数に関する予測値の平均と観測値の平均が等しい性質から導かれます。
■ 公式
$${\bar{e}=\bar{y}-\bar{\hat{y}}=0}$$
Pythonを電卓代わりにして計算してみましょう。
### 基本的な性質b:残差の平均は0になる
print(f'残差の平均:{resid_stats.mean():.10f}')
残差の平均$${\bar{e}}$$は0になりました!
(コンピュータ計算における小数端数処理の関係で、完全な0にはなりません)
c.回帰直線は$${\boldsymbol{x,y}}$$の平均点を通る
説明変数$${x}$$の平均$${\bar{x}}$$と目的変数$${y}$$の平均$${\bar{y}}$$を求めて、回帰直線のグラフにプロットします。
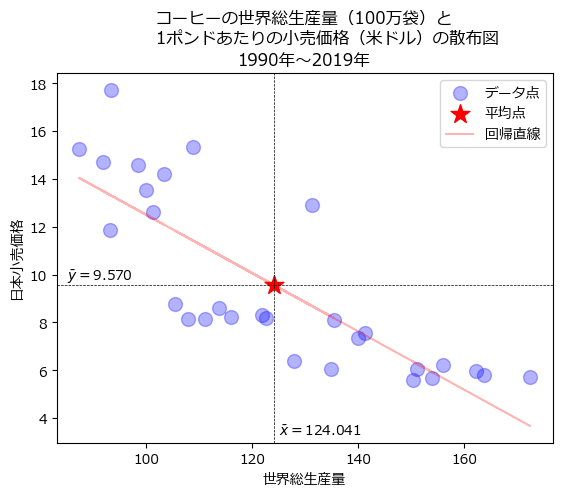
回帰直線(赤い線)は、$${x}$$の平均値$${\bar{x}=124.041}$$と$${y}$$の平均値$${\bar{y}=9.570}$$の点を通っています!
d.予測値$${\boldsymbol{\hat{y_i}=\bar{y}+\hat{\beta}(x_i-\bar{x})}}$$と残差$${\boldsymbol{e_i}}$$の相関係数は0である
$${y_i = \hat{y}_i + e_i}$$の関係の中で、$${\hat{y}_i}$$と$${e_i}$$が無相関ということです。
■ 公式
$${r_{\hat{y},e}=0}$$
Pythonを電卓代わりにして計算してみましょう。
### 基本的な性質d:目的変数の予測値と残差の相関関係は0
np.corrcoef(y_pred_stats, resid_stats).round(10)
1行・2列目、または、2行1列目が予測値と残差の相関係数です。
相関係数$${r_{\hat{y},e}}$$は0になりました!
(コンピュータ計算における小数端数処理の関係で、完全な0にはなりません)

章まとめ
a.目的変数の予測値の平均は観測値の平均と等しいです。
b.残差の平均は0です。
c.回帰直線は説明変数と目的変数の平均点を通ります。
d.目的変数の予測値と残差の相関係数は0です。
3. 線形単回帰モデル
(1) 線形単回帰モデルの数式表現
式2の$${ y = \alpha+ \beta x}$$に確率変数を含めて線形単回帰モデルにバージョンアップします。
説明変数$${x}$$だけでは目的変数$${y}$$を説明しきれない値=誤差の概念を取り入れます。
「誤差項」$${\epsilon}$$を回帰式に追加します。
$$
y_i = \alpha + \beta_i + \epsilon_i, \quad \epsilon_i \sim N(0, \sigma^2), \quad (i=1, 2, \cdots, n)
\tag{10}
$$
(2) 誤差項の前提
誤差項$${\epsilon_i}$$は以下の前提を仮定しています。
これらの仮定は統計検定2級の問題文にさりげなく記載されています。
各誤差項は互いに独立に正規分布に従う(独立性、正規性)
平均は一律0である
分散は一律$${\sigma^2}$$である(等分散性)
統計検定準1級では、誤差(残差)の前提を分析する回帰診断を取り扱っています。
残差診断で用いるプロットの例です。
残差の等分散性、正規性、独立性を確認したり、外れ値の影響の有無を確認します。


章まとめ
線形単回帰モデルは誤差項を取り入れて、回帰式を次のようにバージョンアップしました。
$${y_i = \alpha + \beta_i + \epsilon_i, \quad \epsilon_i \sim N(0, \sigma^2), \quad (i=1, 2, \cdots, n)}$$誤差項は、互いに独立で(独立性)、平均0、同一の分散$${\sigma^2}$$(等分散性)の正規分布に従う(正規性)という仮定があります。
4. 回帰係数の深掘り
(1) 回帰係数の基本統計量
① 傾きの推定量$${\boldsymbol{\hat{\beta}}}$$の期待値と分散
期待値$${E[\hat{\beta}]}$$、分散$${V[\hat{\beta}]}$$は次のとおりです。
$$
E[\hat{\beta}] = \beta
\tag{11}
$$
$$
V[\hat{\beta}] = \cfrac{\sigma^2}{T_{xx}}
\tag{12}
$$
式11より、$${\hat{\beta}}$$は$${\beta}$$の不偏推定量です。
$${\sigma^2}$$は誤差項$${\epsilon_i}$$の分散です。
$${T_{xx}}$$は説明変数$${x}$$の偏差平方和$${\sum^n_{i=1}(x_i-\bar{x})^2}$$です。
② 傾きの推定量$${\boldsymbol{\hat{\beta}}}$$が従う分布
誤差項$${\epsilon_i}$$が正規分布に従っています。
そして、$${\hat{\beta}}$$は、正規分布に従う誤差項$${\epsilon_i}$$の1次式で表現できるので、正規分布に従います。
先程の期待値と分散を用いると、傾きの推定値$${\hat{\beta}}$$のは平均$${\beta}$$、分散$${\sigma^2/T{xx}}$$の正規分布に従うこととなります。
数式で表しましょう。
$$
\hat{\beta} = \cfrac{T_{xy}}{T_{xx}} \sim N \left( \beta, \cfrac{\sigma^2}{T_{xx}} \right)
\tag{13}
$$
③ 傾きの推定量$${\boldsymbol{\hat{\beta}}}$$の標準誤差
式13の分散の公式の$${\sigma^2}$$を$${\hat{\sigma}^2}$$に置き換えて平方根を取ると、$${\hat{\beta}}$$の標準誤差$${\text{se}(\hat{\beta})}$$になります。

$$
\text{se}(\hat{\beta}) = \sqrt{\cfrac{\hat{\sigma}^2}{T_{xx}}} = \cfrac{\hat{\sigma}}{\sqrt{T_{xx}}}
\tag{14}
$$
$${\boldsymbol{\text{se}(\hat{\beta})=\hat{\sigma}/\sqrt{T_{xx}}}}$$は重要なので覚えましょう!
(2) 回帰係数の区間推定・統計的仮説検定
① 誤差項$${\boldsymbol{\epsilon_i}}$$の分散$${\boldsymbol{\sigma^2}}$$の推定量$${\boldsymbol{\hat{\sigma}^2}}$$と標準誤差$${\boldsymbol{\hat{\sigma}}}$$
誤差項$${\epsilon_i}$$の分散の推定量$${\hat{\sigma}^2}$$は、残差$${e_i=y_i-\hat{y}_i}$$の平方和である残差平方和$${\sum^n_{i=1}(y_i-\hat{y}_i)^2}$$を$${n-p-1}$$で割り算して求めます。
標準誤差$${\hat{\sigma}}$$は$${\hat{\sigma}^2}$$の平方根です。
誤差を残差に置き換えて推定している感じです。

$$
\hat{\sigma}^2 = \cfrac{1}{n-p-1}\sum^n_{i=1}(y_i-\hat{y}_i)^2
\tag{15}
$$
$$
\hat{\sigma} = \sqrt{\cfrac{1}{n-p-1}\sum^n_{i=1}(y_i-\hat{y}_i)^2}
\tag{16}
$$
誤差項の標準誤差である$${\boldsymbol{\hat{\sigma} = \sqrt{\cfrac{1}{n-p-1}\sum^n_{i=1}(y_i-\hat{y}_i)^2}}}$$は重要なので覚えましょう!
$${n-p-1}$$は自由度です。
$${n}$$は観測データの数(標本サイズ)、$${p}$$は説明変数の数です。
単回帰の場合、説明変数の数が1なので、自由度は$${n-1-1=n-2}$$です。
重回帰モデルを含めて捉えると誤差項(残差)の自由度は$${\boldsymbol{n-p-1}}$$と覚えておくのがおすすめです。
Pythonを電卓代わりにして計算してみましょう。
### 誤差項の分散の推定量σ^2ハットの計算
# 説明変数の数の設定
p = 1
# 標本サイズの取得
n = data.shape[0]
# 自由度の計算
df_e = n - p - 1
# 分散の推定量σ^2ハットの計算
sigma2_hat_stats = (resid_stats**2).sum() / df_e
# 標準誤差σハットの計算
sigma_hat_stats = np.sqrt(sigma2_hat_stats)
# 表示
print(f'誤差項の分散の推定値: {sigma2_hat_stats:.4f}')
print(f'誤差項の標準誤差 : {sigma_hat_stats:.4f}')
print(f'自由度 : {df_e}')
誤差項の分散の推定値は$${4.8656}$$、標準誤差は$${2.2058}$$です。
② $${\boldsymbol{z}}$$統計量と$${\boldsymbol{t}}$$統計量
確率変数$${\beta}$$の標準化すると$${z}$$統計量を得られます。
$$
z = \cfrac{\hat{\beta}-\beta}{\sqrt{\sigma^2/T_{xx}}} \sim N(0,1)
\tag{17}
$$
上記の式17の分散$${\sigma^2}$$を分散の推定量$${\hat{\sigma}^2}$$に置き換えると$${t}$$統計量を得られます。

$$
t = \cfrac{\hat{\beta}-\beta}{\sqrt{\hat{\sigma}^2/T_{xx}}} \sim t(n-p-1)
\tag{18}
$$
式18中の$${\sqrt{\hat{\sigma}^2/T_{xx}}}$$は標準誤差$${se(\hat{\beta})}$$です。
式18の$${\boldsymbol{t}}$$統計量の公式は重要なので覚えましょう!
Pythonを電卓代わりにして$${t}$$統計量を計算してみましょう。
### t統計量の計算
# βの標準誤差の計算 σ^2ハット/T_xxの平方根
std_err_stats = np.sqrt(sigma2_hat_stats / T_xx)
print(f'βの標準誤差:{std_err_stats:.4f}')
# t統計量の計算 βの推定値/βの標準誤差
t_value_stats = (result_stats.slope - 0) / std_err_stats
print(f't値:{t_value_stats:.4f}')
③ 区間推定
母平均の区間推定のように、傾き$${\beta}$$の区間推定ができます。
$${\alpha}$$は$${1-信頼係数}$$です。
例えば信頼係数$${95\%}$$の場合、$${\alpha=1-0.95=0.05}$$です。
$$
\hat{\beta} \pm t_{\alpha/2}(n-p-1)\sqrt{\cfrac{\hat{\sigma}^2}{T_{xx}}}
\tag{19}
$$
式19中の$${\sqrt{\hat{\sigma}^2/T_{xx}}}$$は標準誤差$${\text{se}(\hat{\beta})}$$です。
Pythonを電卓代わりにして$${\beta}$$の95%信頼区間を計算してみましょう。
### 95%信頼区間の計算
# 信頼区間の%の設定
ci = 0.95
# 初期値
alpha = 1- ci # α
df = n - p - 1 # 自由度
t_ppf = stats.t.ppf(1-alpha/2, df)
# 信頼区間の表示
print(f'{ci:.1%}信頼区間: {result_stats.slope:.4f} ± {t_ppf*std_err_stats:.4f}')
④ 統計的仮説検定
説明変数$${x}$$が目的変数$${y}$$に影響を与えるかどうかをテーマにして統計的仮説検定を行います。
「影響を与える」とは「回帰係数$${\beta}$$がゼロでは無い」ということです。
そこで、主に次の仮説をもって統計的仮説検定を行うようです。
帰無仮説:$${\beta}$$は0である($${H_0:\beta=0}$$)
対立仮説:$${\beta}$$は0ではない($${H_1:\beta \neq 0}$$)
※両側検定です。
検定統計量は$${t}$$統計量です。
帰無仮説$${H_0:\beta=0}$$が正しいとの仮定の下で$${t}$$検定統計量は次にようになります。

$$
t = \cfrac{\hat{\beta}-0}{\sqrt{\hat{\sigma}^2/ T_{xx}}}=\cfrac{\hat{\beta}}{\sqrt{\hat{\sigma}^2/ T_{xx}}} \sim t(n-p-1)
\tag{20}
$$
$${t}$$検定統計量は、回帰係数の推定値$${\hat{\beta}}$$を$${\hat{\beta}}$$の標準誤差$${\text{se}(\hat{\beta})=\sqrt{\hat{\sigma}^2/ T_{xx}}}$$で割り算して求めます。
また、$${t}$$検定統計量は、自由度$${n-p-1}$$の$${t}$$分布に従います。
この部分は重要なので覚えましょう!
Pythonを電卓代わりにして$${\beta}$$の統計的仮説検定を有意水準$${5\%}$$で実施してみましょう。
### 統計的仮説検定
p_value_stats = stats.t.pdf(t_value_stats, df)
print(f'p値: {p_value_stats:.4f}')
$${p}$$値は$${0.00}$$であり、有意水準$${5\%}$$より小さいです。
したがって、有意水準$${5\%}$$で帰無仮説は棄却され、対立仮説「$${\beta}$$は0ではない」と言えます。
コーヒーデータの傾き$${\beta}$$には意味があるのです。

章まとめ
回帰係数の推定値の期待値・分散・標準誤差
$${E[\hat{\beta}] = \beta,}$$
$${V[\hat{\beta}] = \cfrac{\sigma^2}{T_{xx}}}$$
$${se(\hat{\beta}) = \sqrt{\hat{\sigma}^2/T_{xx}}}$$
回帰係数の推定値の$${t}$$統計量
$${t = \cfrac{\hat{\beta}-\beta}{\sqrt{\hat{\sigma}^2/T_{xx}}} \sim t(n-p-1)}$$
$${t}$$統計量が従う$${t}$$分布の自由度は$${n-p-1}$$
$${n}$$は観測データの数(標本サイズ)
$${p}$$は説明変数の数
単回帰の場合$${p=1}$$なので、自由度は$${n-2}$$
回帰係数の推定値の区間推定
$${\hat{\beta} \pm t_{\alpha/2}(n-p-1)\sqrt{\cfrac{\hat{\sigma}^2}{T_{xx}}}}$$
回帰係数の$${t}$$検定統計量
$${t = \cfrac{\hat{\beta}-0}{\sqrt{\hat{\sigma}^2/ T_{xx}}}=\cfrac{\hat{\beta}}{\sqrt{\hat{\sigma}^2/ T_{xx}}} \sim t(n-p-1)}$$
誤差項の分散の推定量と標準誤差
$${\hat{\sigma}^2 = \cfrac{1}{n-p-1}\sum^n_{i=1}(y_i-\hat{y}_i)^2}$$
$${\hat{\sigma} = \sqrt{\cfrac{1}{n-p-1}\sum^n_{i=1}(y_i-\hat{y}_i)^2}}$$
回帰係数、回帰係数の標準誤差、$${t}$$値、$${p}$$値、誤差項の標準誤差は、「統計ソフトウェア」の愛称でおなじみの「R」の回帰分析出力結果に表示されて、試験に出題されることが多いです。
5. 目的変数の平方和の深掘り
(1) 平方和の分解
目的変数の「差」
回帰分析のテーマの1つに「平方和」があります。
目的変数$${y}$$の平均値$${\bar{y}}$$を中心に据えて、観測値$${y_i}$$と予測値$${\hat{y}}$$との関係性を捉える、こんな感じです。
最初に次の図で、平方和を構成する目的変数の「差」を確認しましょう。

■青い垂線
・予測値$${\hat{y}_i}$$(回帰直線上の点)と平均値$${\bar{y}}$$の差です。
・②回帰による平方和に出現する差です。
■赤い垂線
・観測値$${y_i}$$と予測値$${\hat{y}_i}$$の差であり、残差です。
・③残差平方和に出現する差です。
平方和の分解
では平方和の話題に移りましょう。
目的変数$${y}$$に関する次の3つの差の二乗和が平方和の役者です。
平方和の分解に登場する3つの平方和は重要なので覚えましょう。

① 総平方和
観測値$${y_i}$$と平均値$${\bar{y}}$$の差を二乗して合計します。
差は偏差$${y_i - \bar{y}}$$ですので、総平方和は目的変数$${y}$$の偏差平方和です。
総平方和を標本サイズ$${n}$$(または$${n-1}$$)で割り算すると目的変数の分散(または不偏分散)になります。上の図の青い垂線と赤い垂線の和に相当します。
$$
総平方和\ S_T = \sum^n_{i=1}(y_i-\bar{y})^2=T_{yy}
\tag{21}
$$
② 回帰による平方和
予測値$${\hat{y}_i}$$と平均値$${\bar{y}}$$の差を二乗して合計します。
差は上の図の青い垂線に相当します。
$$
回帰による平方和\ S_R = \sum^n_{i=1}(\hat{y}_i-\bar{y})^2
\tag{22}
$$
③ 残差平方和
観測値$${y_i}$$と予測値$${\hat{y}_i}$$の差を二乗して合計します。
差は上の図の赤い垂線に相当します。
$$
残差平方和\ S_e = \sum^n_{i=1}(y_i-\hat{y}_i)^2
\tag{23}
$$
3つの平方和は足し算の関係にあります。
この関係は平方和の分解と呼ばれます。
$$
総平方和\ S_T = 回帰による平方和\ S_R + 残差平方和\ S_e
\tag{24}
$$
平方和の図解
数式が並びましたのでイメージ図で一息入れましょう。
散布図の最も左の観測データ点に注目します。
1996年、世界総生産量$${87.321}$$、日本小売価格$${15.24}$$の点です。
目的変数の差の概念を可視化します。
青い点が観測値、少しだけ映り込んだ赤い斜め線が回帰直線(予測値)、9.570の水平線が平均値です。

③の残差は観測値と予測値の差です。残差平方和に繋がります。
②は予測値と平均値の差です。回帰による平方和に繋がります。
①の偏差は観測値と平均値の差です。②と③の和です。総平方和に繋がります。
続いて差の平方の概念を可視化します。
上の図の「差」を二乗(平方)することは、差の辺を持つ正方形の面積を計算することと同じです。

観測データの全ての点について、①偏差平方(総平方)、②回帰による平方、③残差平方を計算して、それぞれ①②③ごとに合計すると、①総平方和、②回帰による平方和、③残差平方和が算出されます。
このようにして計算された結果は、式24に示される平方和の分解の関係を持っています。
平方和の分解の計算
最後にPythonを電卓代わりにして、平方和の分解の関係を数字で可視化しましょう。
### 平方和の分解
# 総平方和、回帰による平方和、残差平方和の計算
S_T = (y_dev**2).sum()
S_R = ((y_pred_stats - y_mean)**2).sum()
S_e = (resid_stats**2).sum()
# 総平方和
print('総平方和 :', S_T.round(10))
# 回帰による平方和+残差平方和
print('回帰による平方和+残差平方和:', (S_R + S_e).round(10))
コーヒーデータの「総平方和=回帰による平方和+残差平方和」を確認できました。
(2) 決定係数
総平方和に占める回帰による平方和の割合を決定係数$${\boldsymbol{R^2}}$$と呼びます。
次の数式で表現されます。
$$
\begin{align*}
R^2&=\cfrac{S_R}{S_T}=1-\cfrac{S_e}{S_T} \\
\\
決定係数&=\cfrac{回帰による平方和}{総平方和}=1-\cfrac{残差平方和}{総平方和} \\
\\
\end{align*}
\tag{25}
$$
決定係数の意味合い
決定係数$${R^2}$$は「目的変数$${y}$$の変動を表す総平方和$${S_T}$$のうち回帰モデルが説明している程度を示す評価指標」の意味合いがあります。
つまり、決定係数は回帰モデルの当てはまり具合・説明力を示す指標です。
決定係数の値が大きいほど、回帰モデルの当てはまりがよいと言えるでしょう。
決定係数の性質
決定係数$${R^2}$$には次のような性質があります。
① 範囲
$${R^2}$$は$${0 \leq R^2 \leq 1}$$の範囲の値を取ります。
② 説明変数と目的変数の相関係数との関係
最小二乗法で回帰係数を求めた線形単回帰モデルの場合、決定係数$${R^2}$$の平方根$${R}$$は、説明変数$${x}$$と目的変数$${y}$$の相関係数の絶対値$${|r_{xy}|}$$と等しくなります。
③ 目的変数と重相関係数との関係
決定係数$${R^2}$$の平方根$${R}$$は「観測値$${y_i}$$と予測値$${\hat{y}_1}$$の相関係数」です。
この相関係数のことを重相関係数と呼びます。
決定係数の計算
コーヒーデータの決定係数を計算しましょう。
Pythonを電卓代わりにします。
### 決定係数の計算
R2 = S_R / S_T
print(f'決定係数R^2:{R2:.4f}')
$${R^2=0.6607}$$は、まあまあ当てはまりが良いと言えそうです。
相関係数、重相関係数との関係も計算してみましょう。
まずは$${x,y}$$の相関係数から。
### 説明変数xと目的変数yの相関係数の絶対値との関係
# 相関係数の絶対値の取得
r_xy = abs(np.corrcoef(data['世界総生産量'], data['日本小売価格'])[0, 1])
# 決定係数の平方根の取得
R = np.sqrt(R2)
# 表示
print(f'xとyの相関係数: {r_xy:.10f}')
print(f'R2の平方根 : {R:.10f}')
一致しました!
コーヒーデータの線形単回帰モデルは最小二乗法で回帰係数を求めているので、$${x,y}$$の相関係数と決定係数の平方根$${R}$$が等しくなる条件を満たしています。
続いて重相関係数。
### 重相関係数との関係
# 重相関係数の取得
R_y = np.corrcoef(data['日本小売価格'], y_pred_stats)[0, 1]
# 表示
print(f'重相関係数: {R_y:.10f}')
print(f'R2の平方根: {R:.10f}')
こちらも一致しました。
(3) 自由度調整済み決定係数
単回帰分析のときはあまり話題にならないかもですが、決定係数の流れを受けて書きます。
説明変数が複数ある重回帰モデルの場合、説明変数の数$${p}$$を増やすと残差平方和$${S_e}$$が小さくなって、決定係数$${R^2}$$が大きくなる性質があります。
説明変数の数$${p}$$が異なるモデルの比較に利用できるように、決定係数を改造した指標が自由度調整済み決定係数$${R^{*2}}$$です。
総平方和$${S_T}$$と残差平方和$${S_e}$$を自由度で割って調整しています。
$$
R^{*2} = 1 - \cfrac{S_e/(n-p-1)}{S_T/(n-1)}
\tag{26}
$$
コーヒーデータの決定係数を計算しましょう。
Pythonを電卓代わりにします。
### 自由度調整済み決定係数の計算
R_adj = 1 - (S_e/(n - p -1)) / (S_T/(n - 1))
print(f'自由度調整済み決定係数: {R_adj:.4f}')
決定係数$${R^2=0.6607}$$より少し小さな値になりました。
分母の$${S_T/(n-1)}$$の値が相対的に大きくなって、分数の値が大きくなり、1から分数を差し引いた値が小さくなりました。
(4) 回帰の有意性の検定
平方和を用いた統計的仮説検定が回帰の有意性の検定です。
回帰の有意性の検定は「回帰モデルに含まれる複数の説明変数$${x_i}$$の中に目的変数$${y}$$の予測(説明)に役立つ変数があるかどうか」をテーマにする統計的仮説検定です。
回帰係数の検定では(偏)回帰係数1つ1つの有意性を見ましたが、回帰の有意性の検定では回帰モデル全体の効果を見ます。
ちなみに重回帰の場合、回帰係数を「偏回帰係数」と呼びます。
帰無仮説:偏回帰係数$${\beta_i}$$はすべて0である
($${H_0:\beta_1=\cdots\beta_p=0}$$)
対立仮説:偏回帰係数$${\beta_i}$$のどれかが0でない
($${H_1:\beta_1\neq 0\ \text{or}\ \cdots \ \text{or}\ \beta_p \neq 0}$$)
検定統計量は$${F}$$統計量です。
平均平方の比を用いた$${F}$$統計量の数式は次のとおりです。
分母は残差平方和$${S_e}$$を自由度$${n-p-1}$$で割った平均平方、分子は回帰による平方和$${S_R}$$を自由度$${p}$$で割った平均平方です。
$$
F=\cfrac{\cfrac{S_R}{p}}{\cfrac{S_e}{n-p-1}} \sim F(p, \quad (n-p-1))
\tag{27}
$$
分散分析表を用いると検定統計量に用いられる数値をイメージしやすいかもです。
この表を1セット覚えておくとよいと思います!
各平方和と自由度の関係を押さえることができます。

$$
\begin{array}{c|c:c:c:c}
変動要因 & 平方和 & 自由度 & 平均平方 & F \\
\hline
回帰 & S_R & p & V_R = S_R / p & F = V_R / V_e \\
\hdashline
残差 & S_e & n-p-1 & V_e = S_e / (n-p-1) & - \\
\hline
合計 & S_T & n-1 & - & -
\end{array}
$$
コーヒーデータの$${F}$$値を計算して、回帰の有意性の検定を行いましょう。
Pythonを電卓代わりにします。
まず$${F}$$値の計算。結果を分散分析表形式で表示します。
### 回帰の有意性の検定~分散分析表形式
# 自由度の計算
df_S_R = p
df_S_e = n - p - 1
df_S_T = n - 1
# 平均平方の計算
V_R = S_R / df_S_R
V_e = S_e / df_S_e
# F値の計算
F_value_stats = V_R / V_e
### データフレーム化
# 列情報の整理
index_names = ['回帰', '残差', '合計']
sum_squares = [S_R, S_e, S_T]
dfs = [df_S_R, df_S_e, df_S_T]
mean_squares = [V_R, V_e, np.nan]
F_col = [F_value_stats, np.nan, np.nan]
# データフレームの作成
anova_tab = pd.DataFrame({'変動要因': index_names,
'平方和': sum_squares,
'自由度': dfs,
'平均平方': mean_squares,
'F': F_col})
anova_tab.set_index('変動要因', inplace=True)
display(anova_tab.round(4))
続いて有意水準$${5\%}$$で回帰の有意性の検定を行います。
$${F}$$値が従う$${F}$$分布の棄却域と$${F}$$値を比較します。
# 有意水準の設定
alpha = 0.05
# 棄却限界値の計算
c_value_lower = stats.f.ppf(q=alpha/2, dfn=df_S_R, dfd=df_S_e)
c_value_upper = stats.f.ppf(q=1-alpha/2, dfn=df_S_R, dfd=df_S_e)
print(f'棄却域: F値 < {c_value_lower:.4f}, F値 > {c_value_upper:.4f}')
#
if c_value_lower <= F_value_stats <= c_value_upper:
print(f'F値 {F_value_stats:.4f} は棄却域に含まれていない。\n'
f'有意水準{alpha:.1%}で帰無仮説を棄却できない。')
else:
print(f'F値 {F_value_stats:.4f} は棄却域に含まれている。\n'
f'有意水準{alpha:.1%}で帰無仮説を棄却できる。')
有意水準$${5\%}$$で帰無仮説は棄却されました。
「この回帰モデルの回帰係数のどれかはゼロではない」、「説明変数の中に目的変数「日本小売価格」の説明に役立つ変数がある」、と言えます。
$${F}$$分布の確率密度関数のグラフで棄却域を確認しましょう。

$${F}$$分布は左右非対称です。
棄却域は、①左側の棄却限界値の下側と、②右側の棄却限界値の上側です。
$${f}$$値$${=52.5727}$$は②の上側の棄却域に含まれている様子が分かります。

章まとめ
平方和の分解
$${総平方和\ S_T = 回帰による平方和\ S_R + 残差平方和\ S_e}$$
$${総平方和\ S_T = \sum^n_{i=1}(y_i-\bar{y})^2=T_{yy}}$$
$${回帰による平方和\ S_R = \sum^n_{i=1}(\hat{y}_i-\bar{y})^2}$$
$${残差平方和\ S_e = \sum^n_{i=1}(y_i-\hat{y}_i)^2}$$
決定係数$${R^2}$$
$${R^2=\cfrac{S_R}{S_T}=1-\cfrac{S_e}{S_T}}$$
自由度調整済み決定係数$${R^{*2}}$$
$${R^{*2} = 1 - \cfrac{S_e/(n-p-1)}{S_T/(n-1)}}$$
回帰の有意性の検定
帰無仮説:偏回帰係数$${\beta_i}$$はすべて0である
($${H_0:\beta_1=\cdots\beta_p=0}$$)対立仮説:偏回帰係数$${\beta_i}$$のどれかが0でない
($${H_1:\beta_1\neq 0\ \text{or}\ \cdots \ \text{or}\ \beta_p \neq 0}$$)$${F}$$統計量:$${F=\cfrac{\cfrac{S_R}{p}}{\cfrac{S_e}{n-p-1}} \sim F(p, \quad (n-p-1))}$$
分散分析表
$$
\begin{array}{c|c:c:c:c}
変動要因 & 平方和 & 自由度 & 平均平方 & F \\
\hline
回帰 & S_R & p & V_R = S_R / p & F = V_R / V_e \\
\hdashline
残差 & S_e & n-p-1 & V_e = S_e / (n-p-1) & - \\
\hline
合計 & S_T & n-1 & - & -
\end{array}
$$
6. 統計ソフトウェア R の出力結果
(1) R の lm 関数の出力結果
統計検定2級の本試験には、「統計ソフトウェア」による回帰分析の出力結果を読み解く問題が出題されます。
「統計ソフトウェア」は「R」です。
R の lm 関数を用いて回帰分析の結果を出力しています。
コーヒーデータの回帰分析の出力結果は次のようになりました。
lm(formula = 日本小売価格 ~ 世界総生産量, data = data)
Residuals:
Min 1Q Median 3Q Max
-3.4061 -1.5529 -0.0969 1.1879 4.4071
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 24.6786 2.1236 11.621 5.15e-12 ***
世界総生産量 -0.1218 0.0168 -7.251 8.47e-08 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.206 on 27 degrees of freedom
Multiple R-squared: 0.6607, Adjusted R-squared: 0.6481
F-statistic: 52.57 on 1 and 27 DF, p-value: 8.471e-084つのブロックに分けて、出力結果を読み解きましょう。

(2) 目的変数と説明変数の計算式
1つ目のブロックには、目的変数と説明変数の関係を定義した計算式(formula)が表示されています。

(3) 残差
2つ目のブロックは、残差の要約統計量です。
残差は目的変数の観測値と予測値の差です。
最小値・第1四分位数・中央値・第3四分位数・最大値が表示されます。
関連トピックは「残差の平均は0」です。


箱ひげ図で残差の散らばり度合いを確認しましょう。
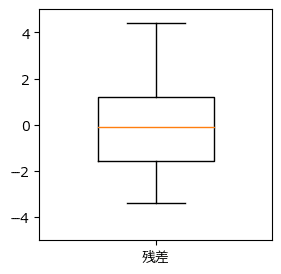
中央値は平均値0とほぼ等しいです。
四分位範囲(第1四分位数から第3四分位数の範囲)はほぼ均等に広がっているように見えます。
最小値と比べて最大値の方が散らばり具合が大きい印象です。
外れ値(ひげの外に位置する点)はありません。
予測値と残差の関係を示す「残差プロット」も確認しましょう。

横軸は目的変数の予測値、縦軸は残差です。
残差は、残差の平均値0を中心にして、ばらついているように見えます。
何らかの傾向、外れ値は無さそうです。
(4) 回帰係数
3つ目のブロックは回帰係数の分析結果です。

切片(Intercept)と切片(説明変数「世界総生産量」)について、次の4項目を表示しています。
回帰係数の推定値:Estimate
回帰係数の標準誤差:Std. Error
$${t}$$値:t value
$${p}$$値:Pr(>| t |)
この回帰分析結果から、回帰式$${y = 24.6786-0.1218x}$$が得られます。
【回帰係数の有意性の検定】を行ってみましょう。
有意水準を$${5\%}$$とします。
■ 切片「Intercept」
切片の$${p}$$値$${5.15e-12=5.15\times 10^{-12}=0.00000000000515}$$は有意水準より小さいです。
切片は有意水準$${5\%}$$で有意です。
つまり、「切片はゼロではない」、「日本小売価格に影響を与えている」と言えます。
■ 傾き「世界総生産量」
傾きの$${p}$$値$${8.47e-08=8.47\times 10^{-8}=0.0000000847}$$は有意水準より小さいです。
傾きは有意水準$${5\%}$$で有意です。
つまり、「傾きはゼロではない」、「世界総生産量は日本小売価格に影響を与えている」、と言えます。
出力結果に回帰係数の関連トピックを付記しましょう。
主要項目には、説明変数$${x}$$と目的変数$${y}$$の「偏差平方和$${T_{xx}}$$や偏差積和$${T_{xy}}$$」が関わっています。
また、「回帰係数÷標準誤差=t値」は出題されやすいトピックです。


ではでは、今まで計算した回帰係数関連の数値と照合してみましょう。
回帰係数の「推定値」は最小二乗法で求めた切片$${24.6786}$$と傾き$${-0.1218}$$と一致しています。
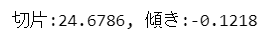
説明変数「世界総生産量」の回帰係数(傾き)の推定値について、標準誤差と$${t}$$値は、回帰係数の深掘りで計算した標準誤差$${0.0168}$$、$${t}$$値$${-7.271}$$と一致しています。

説明変数「世界総生産量」の回帰係数(傾き)推定値の$${p}$$値は、回帰係数の統計的仮説検定で計算した$${p}$$値$${0.0000}$$と一致します。

(5) 平方和・モデル全体
4つ目のブロックは、「平方和」「モデル全体」の分析結果です。
図中の項目名をご参照ください。

上記図中の$${n}$$は観測値の数(標本サイズ)、$${p}$$は説明変数の数です。
【回帰モデルの有意性の検定】を行ってみましょう。
有意水準を$${5\%}$$とします。
$${p}$$値$${8.471e-08=8.471\times 10^{-8}=0.00000008471}$$は有意水準より小さいです。
回帰モデルは有意水準$${5\%}$$で有意です。
つまり、「回帰係数のどれかはゼロではない」、「この回帰モデルの説明変数の中に日本小売価格の説明に役立つ変数がある」、と言えます。
出力結果に平方和・モデル全体の関連トピックを付記しましょう。
主要項目が「平方和$${S_*}$$、自由度、平均平方$${V_*}$$」で繋がっている様子をご覧ください!
目的変数$${y}$$の変動=平方和がさまざまな統計量を繰り出しています。
分散分析表の形式で整理すると覚えやすいでしょう。


ではでは、今まで計算した平方和・モデル全体関連の数値と照合してみましょう。
誤差項の「標準誤差」「自由度」は回帰モデルの誤差項の標準誤差で求めた標準誤差$${2.206}$$、自由度$${27}$$と一致しています。

「決定係数」「自由度調整済み決定係数」は該当章で求めた決定係数$${0.6607}$$と、自由度調整済み決定係数$${0.6481}$$と一致しています。


「$${F}$$値」は回帰の有意性の検定$${F}$$値$${52.57}$$と一致しています。

以上で「統計ソフトウェアの出力結果」の分析を終わりにします。
この出力結果には、単回帰分析のエッセンスがギュッと詰まっていました。

章まとめ
R の出力項目と各章の関連箇所をマッピングしました。
R の出力結果を手がかりにして、数値の意味合い、数値間の関係、裏付けになる計算式を整理して、オリジナルの単回帰モデルノートを作ってみてはいかがでしょう。

第1部はこれで終了です。
長旅、お疲れ様でした!
第2部は複数のツールを利用して単回帰分析を実践します。
お楽しみに🌸
第2部へ続く
ブログの紹介
noteで3つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
2.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。
3.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、、Pythonのコラムを不定期に綴っています。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
