7-1 推定値と標準誤差 ～ 母比率の点推定と標準誤差、ときどき、都道府県別スポーツ実施状況

今回の統計トピック

「統計的推定」の分野に進みます。
今回は母比率の推定値と標準誤差を数式表現で求めます。
「実践する」では、全国の都道府県のスポーツ実施状況を深掘りします。
久しぶりに政府統計「e-Stat」の統計データを活用します！

公式問題集の準備

「公式問題集」の問題を利用します。お手元に公式問題集をご用意ください。
公式問題集が無い場合もご安心ください！
「知る」「実践する」の章で、のんびり統計をお楽しみください！

日本統計学会公式認定　統計検定　2級　公式問題集［CBT対応版］

問題を解く

---

📘公式問題集のカテゴリ

推定の分野
問1 推定値と標準誤差（過去１年間に野球を行った15歳以上の割合）

試験実施年月
統計検定2級 2018年6月 問11（回答番号23）

問題

公式問題集をご参照ください。

解き方

題意
次表を参考にしながら、２道県で野球をした人の母比率の推定値$${\hat{p}}$$と標準誤差$${\text{se}(\hat{p})}$$を数式表現で解答します。
なお、推定人口は真の人口と仮定されています。

$$
\begin{array}{c:cc}
項目 & 北海道(i=1) & 沖縄県(i=2) \\
\hline
15歳以上推定人口: N_i & 4,542千人 & 1,150千人  \\
標本の大きさ: n_i& 4,633人 & 2,849人  \\
野球をした人の率: \hat{p_i} & 7.1\% & 9.2\%  \\
\end{array}
$$

公式問題集の記述を改変

日本地図のイラスト：「いらすとや」さんより

２道県を母集団とし、母比率の推定値、分散、標準誤差を求めます。

■母比率$${p}$$
母集団である２道県の推定人口のうち、実際に野球をした人の人数の割合が母比率になります。

$$
\begin{align*}
&母比率 \\
 \\
&=\cfrac{(北海道の人口\times 野球した率)+(沖縄県の人口\times 野球した率)}{北海道の人口＋沖縄県の人口}
\end{align*}
$$

母比率を$${p}$$、北海道の野球をした人の母比率を$${p_1}$$、沖縄県の野球をした人の母比率を$${p_2}$$、北海道の推定人口を$${N_1}$$、沖縄県の推定人口を$${N_2}$$とすると、上の式はシンプルになります。

$$
p=\cfrac{N_1 p_1+N_2 p_2}{N_1+N_2}
$$

■母比率の推定値$${\hat{p}}$$
母比率の推定値を$${\hat{p}}$$、北海道の野球をした人の標本比率を$${\hat{p_1}}$$、沖縄県の野球をした人の標本比率を$${\hat{p_2}}$$とし、上の式を母比率の推定値に変換します。

$$
\hat{p}=\cfrac{N_1 \hat{p_1}+N_2 \hat{p_2}}{N_1+N_2}
$$

（ア）の解答は$${\cfrac{N_1 \hat{p_1}+N_2 \hat{p_2}}{N_1+N_2}}$$です。

野球選手の男の子のイラスト（将来の夢）：「いらすとや」さんより

■次のステップ

標準誤差$${\text{se}(\hat{p})}$$は、分散の推定量$${\hat{V}[\hat{p}]}$$の平方根です。
まず、母比率の推定値$${\hat{p}}$$の分散$${V[\hat{p}]}$$を求め、次に分散の推定量の平方根である標準誤差$${\text{se}(\hat{p})}$$を計算します。

元気に階段を上る男性のイラスト：「いらすとや」さんより

■分散$${V[\hat{p}]}$$
上の計算で求めた母比率の推定値$${\hat{p}=\cfrac{N_1 \hat{p_1}+N_2 \hat{p_2}}{N_1+N_2}}$$を$${V[\hat{p}]}$$に当てはめるところから始めます。
途中で、次の公式を利用します

①分散の公式：$${V[aX]=a^2V[X]}$$
②標本比率$${\hat{p}}$$の分散の公式：$${V[\hat{p}]=\cfrac{p(1-p)}{n}}$$

なお、問題文より、北海道の標本の大きさは$${n_1}$$、沖縄県の標本の大きさは$${n_2}$$であり、$${\hat{p_1},\hat{p_2}}$$は独立です。

$$
\begin{align*}
V[\hat{p}]&=V\left[\cfrac{N_1 \hat{p_1}+N_2 \hat{p_2}}{N_1+N_2}\right] \\
  \\
&=V \left[ \cfrac{N_1 \hat{p_1}}{N_1+N_2}+\cfrac{N_2 \hat{p_2}}{N_1+N_2}\right] \\
  \\
&=V \left[ \cfrac{N_1 }{N_1+N_2}\ \hat{p_1}+\cfrac{N_2}{N_1+N_2}\ \hat{p_2}\right] \\
  \\
&=V \left[ \cfrac{N_1 }{N_1+N_2}\ \hat{p_1}\right]+V\left[\cfrac{N_2}{N_1+N_2}\ \hat{p_2}\right] \\
  \\
&=\left(\cfrac{N_1 }{N_1+N_2} \right)^2 V \left[ \hat{p_1}\right]+ \left(\cfrac{N_2}{N_1+N_2} \right)^2V\left[\hat{p_2}\right]   \cdots 公式① \\
  \\
&=\left(\cfrac{N_1 }{N_1+N_2} \right)^2 \cfrac{p_1(1-p_1)}{n_1}+ \left(\cfrac{N_2}{N_1+N_2} \right)^2\cfrac{p_2(1-p_2)}{n_2}  \cdots 公式②\\
\end{align*}
$$

分散が求まりました。
あとひといき！

■標準誤差$${\text{se}(\hat{p})}$$
北海道と沖縄県の母比率$${p_1, p_2}$$を標本比率$${\hat{p_1},\hat{p_2}}$$に置き換えて分散の推定量を求めて、平方根をとります。

$$
\text{se}(\hat{p})=\sqrt{\left(\cfrac{N_1 }{N_1+N_2} \right)^2 \cfrac{\hat{p_1}(1-\hat{p_1})}{n_1}+ \left(\cfrac{N_2}{N_1+N_2} \right)^2\cfrac{\hat{p_2}(1-\hat{p_2})}{n_2}}
$$

標準誤差が求まりました。
（イ）の解答は$${\sqrt{\left(\cfrac{N_1 }{N_1+N_2} \right)^2 \cfrac{\hat{p_1}(1-\hat{p_1})}{n_1}+ \left(\cfrac{N_2}{N_1+N_2} \right)^2\cfrac{\hat{p_2}(1-\hat{p_2})}{n_2}}}$$です。

スポーツで余暇を楽しむことって、素敵です！

野球のキャラクター：「いらすとや」さんより

解答

② です。

難易度　ふつう

・知識：母比率、標本比率、標準誤差
・計算力：数式組み立て（低）、数式計算（中）
・時間目安：2分

知る

---

おしながき

公式問題集の問題に接近してみましょう！
ここでは「2021年の北海道と沖縄県の野球行動者の割合データ」を利用します。
野球行動者は、過去１年間にキャッチボールを含む野球を行った15歳以上の人です。

【出典記載】
出典：「令和３年社会生活基本調査結果」（総務省統計局、URL: https://www.e-stat.go.jp/stat-search/files?stat_infid=000032223345）
【コンテンツ編集・加工の記載】
記事の記載にあたっては、出典記載の「令和３年社会生活基本調査結果」（総務省統計局）を加工して作成しています。

標準誤差

標準誤差、母比率・標本比率の概要をざっと確認してから、2021年のデータを用いて公式問題集の類似問題を解きましょう。

📕公式テキスト：3.3.1 点推定（107ページ）
公式テキストでは、標本平均などの推定量（値）のばらつきを示す指標として「標準誤差」を紹介しています。

（母平均における標本平均・中央値・刈込み平均などのように、一致推定量が複数あるとき）
一致推定量どうしを比較するのであれば、ばらつきが小さな推定量のほうが優れている。ただし、推定量$${\theta}$$の分散は未知である。
そこで分散の推定量$${\boldsymbol{\hat{V}[\hat{\theta}]}}$$の平方根が用いられる。 これを標準誤差とよび、$${\text{se}(\hat{\theta})}$$あるいは単に$${\text{se, s.e.}}$$などと表す。

公式テキストより引用（太字は加工）

公式テキストの脚注によると、標準誤差の定義には次の２つの流儀があるそうです。

1. 推定量の標準偏差$${\{V[\hat{\theta}]\}^{1/2}}$$

2. 推定量の標準偏差$${\{V[\hat{\theta}]\}^{1/2}}$$の推定値（公式テキストが採用）

標本平均の標準誤差

標準誤差といえば、一般に、標本平均の標準誤差を示す印象です。
標本平均$${\bar{x}}$$の標準誤差$${\text{se}(\bar{x})}$$を求めてみましょう。

1. 標本平均の分散$${V[\bar{x}]=\sigma^2/n}$$の母分散$${\sigma^2}$$を推定量（値）$${\hat{\sigma}^2}$$で置き換えます。

2. 1. で求めた$${\hat{V}[\bar{x}]=\hat{\sigma}^2/n}$$の平方根を取ります。

3. $${\text{se}(\bar{x})=\hat{\sigma}/\sqrt{n}}$$の出来上がり！

なお、母分散の推定量（値）$${\hat{\sigma}^2}$$は不偏分散です。
$${\hat{\sigma}^2=\cfrac{1}{n-1}\displaystyle \sum^n_{i=1}(x_i-\bar{x})^2}$$

（例）
サンプルサイズ$${n=64}$$、標本平均$${\bar{x}=50}$$、標本分散$${\hat{\sigma}^2=16}$$のとき、標準誤差$${\text{se}(\bar{x})=\hat{\sigma}/\sqrt{n}=\sqrt{16}/\sqrt{64}=4/8=0.5}$$です。
母平均の推定値（標準誤差付き）は$${50 \pm 0.5}$$です。

平均台のイラスト（体操）：「いらすとや」さんより

母比率・標本比率

📕公式テキスト：3.4.4 母比率の推定（118ページ～）
母集団における何かの割合が母比率$${p}$$です。
テレビの視聴率、内閣支持率などが母比率の例です。

母比率$${p}$$の推定量として標本比率$${\hat{p}=x/n}$$を考えます。
$${x}$$は何かに該当する数（確率変数）です。あるテレビ番組を見た人数、内閣を支持する人数などです。
$${n}$$はサンプルの大きさです。100人を調査した場合、$${n=100}$$です。

標本比率$${\hat{p}}$$の期待値、分散、標準誤差は次のようになります。

・期待値$${E[\hat{p}]=p}$$
・分散$${V[\hat{p}]=\cfrac{p(1-p)}{n}}$$
・標準誤差$${\text{se}(\hat{p})=\sqrt{\cfrac{\hat{p}(1-\hat{p})}{n}}}$$

黄金比のイラスト：「いらすとや」さんより

2021年のデータを調べる

2021年（令和3年）の社会生活基本調査の調査結果データから、全国、北海道、沖縄について、ふだんのスポーツの行動状況を抜き出しました。

出典：「令和３年社会生活基本調査結果」（総務省統計局）より抜粋

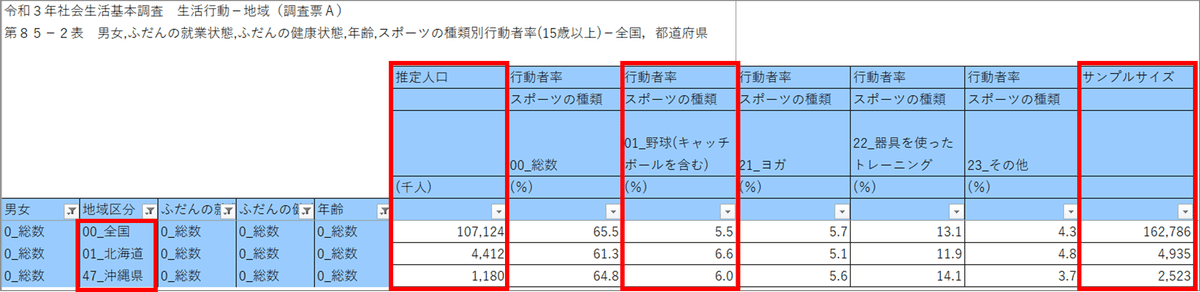
ちなみに調査票（抜粋）は次のような感じです。
スポーツを行った日数を質問しているようです。

出典：「令和３年社会生活基本調査 調査票A」（総務省統計局）より抜粋

2021年の調査結果から、北海道と沖縄県の過去１年間に野球を行った15歳以上の割合等のデータをまとめました。

$$
\begin{array}{c:cc}
項目 & 北海道(i=1) & 沖縄県(i=2) \\
\hline
15歳以上推定人口: N_i & 4,412千人 & 1,180千人  \\
標本の大きさ: n_i& 4,935人 & 2,523人  \\
野球をした人の率: \hat{p_i} & 6.6\% & 6.0\%  \\
\end{array}
$$

2016年（平成28年）調査結果とくらべます。
15歳以上の推定人口は、北海道が130千人減少、沖縄県が30千人増加しています。
野球をした人の率は、北海道が0.5ポイント減少、沖縄県が3.2ポイント減少しています。

類似問題です

それでは、2021年データに基づいて、北海道と沖縄県の２道県合計について、野球を行った人の母比率の推定値と標準誤差を算出しましょう！

クエスチョンマークの帽子を被っている女性のイラスト：「いらすとや」さんより

まずは母比率の推定値から。

$$
\begin{align*}
&母比率の推定値 \\
 \\
&=\cfrac{(北海道の人口\times 野球した率)+(沖縄県の人口\times 野球した率)}{北海道の人口＋沖縄県の人口} \\
  \\
&=\cfrac{4412 \times 0.066+1180 \times 0.060}{4412+1180} \\
  \\
&=\cfrac{361.992}{5592} \\
  \\
&=\cfrac{361.992}{5592} \\
  \\
&=0.0647 \cdots \\
\end{align*}
$$

母比率の推定値は$${6.5\%}$$です。
2018年は 7.5% であり、5年間で 1 ポイント減少しています。

続いて標準誤差です。

$$
\begin{align*}
&北海道=(北海道人口割合)^2\times \cfrac{北海道野球率\times (1-北海道野球率)}{北海道サンプルサイズ} \\
  \\
&沖縄県=(沖縄県人口割合)^2\times \cfrac{沖縄県野球率\times (1-沖縄県野球率)}{沖縄県サンプルサイズ} \\
  \\
&標準誤差=\sqrt{北海道+沖縄県} \\
  \\
&=\sqrt{\left(\cfrac{4412}{4412+1180} \right)^2\cfrac{0.066\times(1-0.066)}{4935}+\left(\cfrac{1180}{4412+1180} \right)^2\cfrac{0.060\times(1-0.060)}{2523}} \\
  \\
&=\sqrt{\left(\cfrac{4412}{5592}\right)^2 \times \cfrac{0.061644}{4935}+\left(\cfrac{1180}{5592}\right)^2 \times \cfrac{0.0564}{4935}} \\
  \\
&=0.00296 \cdots
\end{align*}
$$

標準誤差は 0.3 ポイントです。
北海道＋沖縄県の野球行動者の比率は$${6.5\% \pm 0.3ポイント}$$です。

日本は野球が盛んな国だと思っていましたが、大人の野球の競技人口はそれほど多くないようです。
一方で観戦者数は多いのでしょう。
高校野球、プロ野球、大リーグなどを観戦して、わいわい応援するのも楽しいですね！

野球の応援のイラスト：「いらすとや」さんより

実践する

---

スポーツを通じて統計を掘り下げてみよう！

今回は豪華二本立てです！
①手作業やEXCELを用いて、母比率の推定値と標準誤差の計算を実践します。
②EXCELとPythonを利用して、日本のスポーツ実践の特色を調査します。

「2021年の北海道と沖縄県の野球行動者の割合データ」は政府統計の総合窓口「e-Stat」で公開されています。

政府統計の総合窓口

総務省統計局の「社会生活基本調査」で作成される統計データです。
５年ごとに実施されているそうです。

統計局ホームページ/令和3年社会生活基本調査の概要

次のリンクでダウンロードサイトを開くことができます。
「表示・ダウンロード」をクリックすると、EXCELファイル（ファイル名：a085_2.xlsx）をダウンロードできます。

社会生活基本調査 85-2 男女,ふだんの就業状態,ふだんの健康状態,年齢,スポーツの種類別行動者率(15歳以上)－全国，都道府県 | ファイル | 統計データを探す | 政府統計の総合窓口

EXCELファイルの顔つきはこんな感じ。

出典：「令和３年社会生活基本調査結果」（総務省統計局）より抜粋

CSVファイルのダウンロード
こちらのリンクから「2021年の都道府県別・スポーツの種類別行動者の割合データ」のCSVファイルをダウンロードできます。
Pythonサンプルファイルを利用する方は、このCSVファイルをダウンロードしてください。

sample_data.csv

6.29 KB

ファイルダウンロードについて

ダウンロード

電卓・手作業で作成してみよう！

上述の方法でデータを取得して、または、「知る」に掲載の数値を利用して、電卓やそろばんをはじいて、手作業で母比率と標準誤差を計算してみましょう！
一番記憶に残る方法ですし、試験本番の電卓作業のトレーニングにもなります。

メモ帳のイラスト（文房具）：「いらすとや」さんより

EXCELで作成してみよう！

データ数が多い場合、やはり手作業では非効率になります。
パソコンを利用して、手早く作表できるようになれば、実務活用がしやすくなるでしょう。

計算シートの紹介

素データから都道府県とスポーツを選択して、母比率と標準誤差を計算するシートです。
さまざまな都道府県の組み合わせを入力して、スポーツの盛り上がりの状況を確認してみましょう！

入力サンプル

パラメータ入力欄の「都道府県１」「都道府県２」「スポーツ」は入力規制機能を利用して、ドロップダウンリストで選択できます。

■「データの入力規則」画面の概要
メニューパス
「メニュー」＞「データ」＞「データツール」＞「データの入力規制」

データの入力規制画面サンプル

標本サイズ、行動者率、推定人口は、VLOOKUP関数で別シートの素データから取得しています。

VLOOKUP関数の使用例

データを分析

お題を変えます！データ分析に移ります！

スポーツの種類を全国の各行動者率の高い順に並べました。
全国的に行動者の多い高いスポーツが分かります。

出典：「令和３年社会生活基本調査結果」（総務省統計局）を加工

ダントツはウォーキング等。
続いて、器具利用（フィットネス？）、ジョギング等、サイクリング、登山等、つり、ゴルフなど。
上位には、ひとり時間を楽しむスポーツが多い印象です。

団体スポーツでは、野球がトップ。
WBCの熱狂が続いて、これから野球をプレイする人が増えるかもしれませんね（希望的観測）。

グループウォーキングのイラストの（帽子付き）：「いらすとや」さんより

野球、サッカー、ウォーキング等について、都道府県別の人口と行動者率の散布図を作りました。
人口とスポーツ行動者率との間に、何か傾向を見つけられたでしょうか？

出典：「令和３年社会生活基本調査結果」（総務省統計局）を加工

EXCELサンプルファイルのダウンロード
こちらのリンクからEXCELサンプルファイルをダウンロードできます。

7-1_推定値と標準誤差.xlsx

55.1 KB

ファイルダウンロードについて

ダウンロード

Pythonで作成してみよう！

プログラムコードを読んで、データを流したりデータを変えてみたりして、データを追いかけることで、作表ロジックを把握する方法も効果的でしょう。
サンプルコードを揃えておけば、類似する作表作業を自動化して素早く結果を得ることができます。

今回は、全国のスポーツ行動の傾向をグラフで探ります。
「2021年の都道府県別・スポーツの種類別行動者の割合データ」を利用します。

①インポート

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'MS Gothic'
%matplotlib inline

②csvファイルの読み込み

まず、上述のダウンロードリンクより、CSVファイルをダウンロードします。
その後、次のコードを実行して、CSVファイルをpandasのデータフレームに読み込みます。

datafile = './sample_data.csv' # CSVファイルの格納フォルダとファイル名を設定
df = pd.read_csv(datafile)
col_list = df.columns.values
print(df.shape)
display(df.head())

出力イメージ

③都道府県別のスポーツ実施状況

プロット用の関数を定義します。

# 都道府県別スポーツ行動率のプロット関数（１スポーツを指定）
def sports_act_rate_plot(col, lower=None, upper=None):
    fig, ax = plt.subplots(figsize=(12, 4), tight_layout=True)
    df_play = df.iloc[1:][['都道府県', col]].sort_values([col], ascending=False)
    plt.bar(df_play['都道府県'], df_play[col])
    plt.axhline(df.iloc[0][col], c='red', lw=1, ls='--', label=f'全国平均: {df.iloc[0][col]}%')
    fig.autofmt_xdate(rotation=45)
    plt.ylabel('行動者率(%)')
    if lower is not None:
        plt.ylim([lower, upper])
    plt.title(f'{col} - 2021年 都道府県別 スポーツの種類別行動者率')
    plt.legend()
    plt.show()

■スポーツ行動率の高い都道府県を探索
さあ、最もスポーツ行動率が高い都道府県はどこでしょう？

# スポーツ行動率の高い都道府県の順にプロット
col = '00_総数'
sports_act_rate_plot(col, 45, 75)

出力イメージ

トップ５は、東京都、神奈川県、埼玉県、愛知県、千葉県です。
首都圏の割合が高いみたいです。
全国平均は６５％。半数以上の人が１年の間にスポーツを行ったようです。

■スポーツ間の行動率の傾向を探索

２つのスポーツの相関関係を確認しましょう。
緑色は正の相関、橙～赤色は負の相関です。

# スポーツの種類間の相関係数　ヒートマップ
plt.figure(figsize=(15, 6)) 
sns.heatmap(df.iloc[:, 3:26].corr(numeric_only=True), cmap='RdYlGn', 
            vmin=-1, center=0, vmax=1, annot=True, fmt='.2f');

出力イメージ

正の相関（両方のスポーツの行動傾向が近い）

• 「サイクリング」・「ジョギング・マラソン」・「ウォーキング・軽い運動」・「ヨガ」・「器具を使ったトレーニング」は正の相関が強めです。

• 「サッカー」と「ジョギング・マラソン」も正の相関が強めです。

負の相関（両方のスポーツの行動傾向が逆）

• 「つり」と「登山・ハイキング」「サイクリング」は負の相関が強めです。

■正の相関関係の強いスポーツの例
「サイクリング」と「ウォーキング・軽い体操」

# サイクリングとウォーキング・軽い体操の都道府県別の傾向
col = '18_サイクリング'
sports_act_rate_plot(col)
col = '20_ウォーキング・軽い体操'
sports_act_rate_plot(col)

出力イメージ

上位どうし、下位どうしに同一の都道府県が現れています。
首都圏が上位、東北・九州が下位に寄っている感じがします。

■負の相関関係の強いスポーツの例
「つり」と「登山・ハイキング」

# つりと登山・ハイキングの都道府県別の傾向
col = '14_つり'
sports_act_rate_plot(col)
col = '17_登山・ハイキング'
sports_act_rate_plot(col)

出力イメージ

つりの上位、広島県・愛媛県・熊本県は、登山等の中位～下位です。
一方で、登山・ハイキングの上位、東京都・神奈川県は、つりの下位です。
東京都・神奈川県の登山・ハイキング人気は意外でした。

④人口とスポーツの関係の探索

人口の多い都道府県とスポーツの種類の関係を確認します。
箱ひげ図で１５歳以上推定人口の分布状況を見てみましょう。

# 都道府県別15歳以上推定人口の四分位数を確認
display(df.iloc[1:]['推定人口'].quantile(q=[0, 0.25, 0.5, 0.75, 1]))
plt.boxplot(df.iloc[1:]['推定人口'], vert=False);

四分位数

出力イメージ

・全体の上位25%都道府県の15歳以上推定人口は2,277千人
・外れ値の都道府県は８つ

トップ５（6,000千人以上）の都道府県を赤色にマーキングして、スポーツと人口の多さの関係を可視化してみましょう。

# トップ５の一覧
threshold = 6000 # 15歳以上推定人口トップ5
df[df[col_list[1]] > threshold].iloc[1:].sort_values([col_list[1]], ascending=False)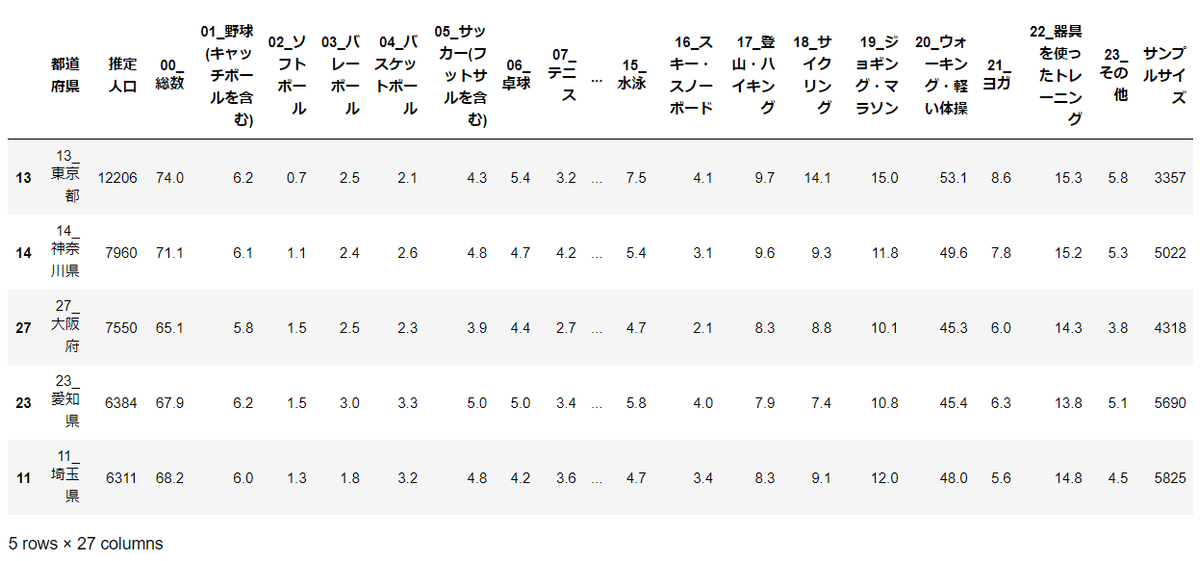

出力イメージ

■スポーツ別の行動率が高い都道府県順プロット

プロット用の関数を定義します。

# 都道府県別スポーツ行動率のプロット関数（複数スポーツを指定、人口トップ５都道府県は赤色）
def sports_act_rate_plot2(cols):
    for col in cols: 
        all_mean = df.iloc[0][col]
        df2 = df.iloc[1:][[col_list[0], col, col_list[1]]]
        df2[col_list[0]] = df2[col_list[0]].str[3:]
        df2 = df2.sort_values([col], ascending=False)
        color = ['red' if num > threshold else 'steelblue' for num in df2[col_list[1]]]

        fig, ax = plt.subplots(figsize=(12, 4), tight_layout=True)
        plt.bar(df2[col_list[0]], df2[col], color=color)
        plt.axhline(all_mean, c='red', lw=1, ls='--', label=f'全国平均: {all_mean}%')
        fig.autofmt_xdate(rotation=45)
        plt.ylabel('行動者率(%)')
        plt.title(f'{col[3:]} - 2021年 都道府県別 スポーツの種類別行動者率')
        plt.legend()
        plt.show()

cols にリスト形式でスポーツの種類を指定して、グラフを表示します。
次のコードは野球、ソフトボール、バレーボール、バスケットボール、サッカーの５種のグラフを出力するサンプルです。

cols = [ '01_野球(キャッチボールを含む)', '02_ソフトボール', '03_バレーボール',
             '04_バスケットボール', '05_サッカー(フットサルを含む)' ]
sports_act_rate_plot2(cols)

出力イメージは省略します。

人口トップ５の都道府県（赤色）で人気のスポーツをいくつかグラフで確認しましょう。

■サッカー

■サイクリング

■ヨガ

■器具を使ったトレーニング

次は人口のトップ５の都道府県で行動率の低いスポーツをいくつかグラフで確認しましょう。

■バレーボール

■グラウンドゴルフ

■つり

スポーツを行うことについて、都道府県ごとに特色がありそうな感じがしました。
みなさんのお住まいの地域では、どんなスポーツが盛んですか？

Pythonサンプルファイルのダウンロード
こちらのリンクからJupyter Notebook形式のサンプルファイルをダウンロードできます。

7-1_推定値と標準誤差.ipynb

4.96 MB

ファイルダウンロードについて

ダウンロード

---

おわりに

今回から「推定の分野」が始まりました。
推定の分野には、特定の値を推定する「点推定」と、一定の幅を推定する「区間推定」が含まれます。
今回は母比率の値を点推定しました。
次回は不偏推定量の話題です。数式です。。。

最後までお読みいただきまして、ありがとうございました。

---

のんびり統計シリーズの記事

次の記事

前の記事

目次