
数学とPython 7 マクローリン展開 ~可視化
はじめに
シリーズ数学とPythonのご案内
「シリーズ数学とPython」は、数学の学習中に「解けない、無理~」と焦ったときに、Pythonで数値の動きや可視化を行って、理解の糸口を見つけたときのことを記事にします。
データサイエンス数学ストラテジスト上級公式問題集
この記事は「データサイエンス数学ストラテジスト上級公式問題集」の問題の解読中に見つけたヒントを取り扱います。
今回取り組む問題
問題37「関数のマクローリン展開-微分の達人になろう!」
Python実装
やりたいこと
問題で与えられた1変数関数$${f(x)}$$をマクローリン展開して、グラフを描画します。
実は、自分が解いた答案が、公式問題集に記載の解答・解説と合わなかったので、Pythonの力を借りて計算の検算を試みたのです。
その後、解答・解説の記載に誤植があったことを正誤表で見つけました(納得)。
作戦
sympy を用いて、公式問題集の出題内容($${x^4}$$の係数)をサクッと確かめてから、グラフを描画します。
実装の開始
インポート
### インポート
import sympy
sympy.init_printing;関数$${\boldsymbol{f(x)}}$$の定義
### 変数、関数の定義
# 変数xの定義
sympy.var('x')
# 出題の関数f(x)を定義
question_fx = sympy.sqrt(1 -x +2*x**2)
display(question_fx)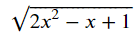
関数$${\boldsymbol{f(x)}}$$をマクローリン展開する
sympy の series (ベキ級数展開)でマクローリン展開を行います。
【関数$${f(x)}$$のマクローリン展開】
$${f(x)}$$の第$${n}$$次導関数を$${f^{(n)}(x)}$$とするとき、
$${f(x) \\ = f(0) + \cfrac{f^{(1)}(0)}{1!}x + \cfrac{f^{(2)}(0)}{2!}x^2 + \cfrac{f^{(3)}(0)}{3!}x^3 + \cdots + \cfrac{f^{(n)}(0)}{n!}x^n + \cdots \\ =\sum^{\infty}_{k=0} f^{(k)}(0) \cfrac{x^k}{k!} }$$
引数 n=5 と設定することで、$${x^4}$$まで展開します。
$${x^5}$$以降は剰余項$${O(x^5)}$$にまとまります。
### f(x)をマクローリン展開する
answer_me = sympy.series(question_fx, x, n=5) # n:展開する指数+1
display(answer_me)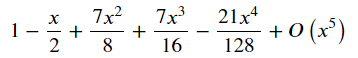
$${x^4}$$の係数は$${-\cfrac{21}{128}}$$でした。
マクローリン展開の結果をプロット
sympy の plot でグラフを描画します。
removeOメソッドで余剰項を除去します。
### マクローリン展開の結果をプロットする removeO():剰余項O()を削除
sympy.plot(answer_me.removeO(), question_fx, legend=True, ylim=(-8, 8));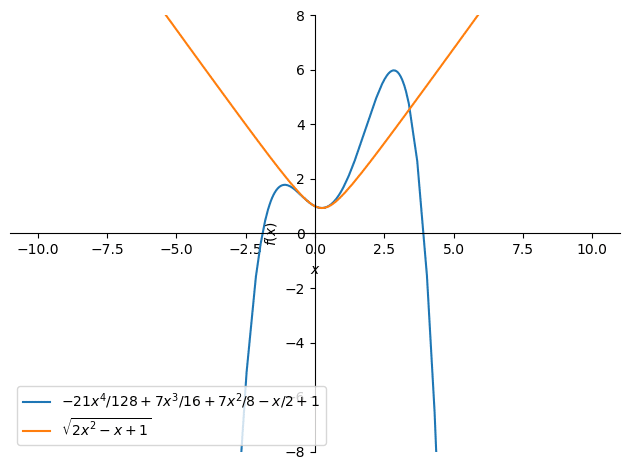
ブルーの曲線がマクローリン展開で得た式です。
峰が2つあります。
魚が水面から顔を出している感じがします🦈
オレンジの曲線は元の関数$${f(x)}$$です。
ブルーの曲線の凹の部分(魚の口)に当てはまっています。
今回も可視化できてよかったです!
(数式と比べて優しい温もりを感じます😉)
参考:テーラー展開
sympy の series は 引数 x0 に$${a}$$の値を指定することで、テーラー展開を行えます。
出題の関数$${f(x)}$$を$${x=1}$$の周りでテーラー展開してみます。
引数 x0=1 とします。
### f(x)をテーラー展開する f(x)=question_fx, x=a, a=x0=1
sympy.series(question_fx, x=x, x0=1, n=5)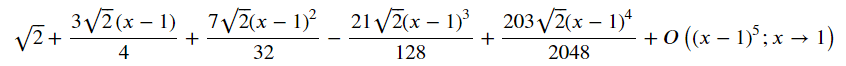
おまけ
Pythonで問題集の問題を解くコードです。
Jupyter Notebook のセル(計算ステップ)ごとに、計算結果を表示しています。
### インポート
import sympy
sympy.init_printing;### 変数、関数の定義
# 変数xの定義
sympy.var('x')
# 関数f(x)の定義
f = sympy.sqrt(1 -x + 2*x**2)
f### 微分を繰り返す
# 1回目
f_d1 = sympy.diff(f, x)
f_d1# 2回目
f_d2 = sympy.diff(f_d1, x)
f_d2# 3回目
f_d3 = sympy.diff(f_d2, x)
f_d3# 4回目
f_d4 = sympy.diff(f_d3, x)
f_d4### 4階微分の結果を整理(因数分解)
f_d4_fact = sympy.factor(sympy.expand(f_d4))
f_d4_fact### (おまけ)4階微分を一括して実行する方法 diffの第3引数でn階微分を指定
sympy.factor(sympy.diff(f, x, 4))### 第4次導関数f_d4_factのxに0を代入
f_d4_fact_0 = f_d4_fact.subs(x, 0)
f_d4_fact_0### f(^4)(0) / 4! を計算する ★解答
f_4_coef = f_d4_fact_0 / sympy.factorial(4)
f_4_coefおわりに
自力の計算結果をsympyで検証することができました。
おわり
ブログの紹介
noteで3つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
2.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。
3.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
