
シリーズPython⑤ Pythonによるベイズ統計モデリングを PyMC Ver.5で
はじめに
Pythonによるベイズ統計モデリングの紹介
この記事は書籍「Pythonによるベイズ統計モデリング PyMCでのデータ分析実践ガイド」(共立出版、以下「テキスト」と呼びます)を PyMC Ver.5 で実践したときの留意点を取り扱います。
このテキストは、以前実践した「あたらしいベイズ統計の教科書」(以下「教科書」と呼びます)終了後の次ステップに最適なPython&ベイズ統計の書籍です。
「教科書」の復習、ベイズ統計の考え方の深掘り、「モデル比較」「混合モデル」「ガウス過程」という新しい領域のチャレンジを含みます。
豊富なPythonコードを動かしながら、MCMCのコード、予測の評価などを学びます。
■ テキストのPyMC3コードをPyMC Ver.5で動かす
この記事は、テキストの PyMC3 のコードを「PyMC Ver.5」に変換して動かす際に、変換が難しいと感じたことを記載しています。
まず第5章です。
Theano から PyTensor への書き換えや、traceオブジェクトの操作に関して、手間取ったコードを取り上げました。
続いて第8章です。
ガウス過程の PyMC 処理にて、おかしなアウトプットになってしまったことを取り上げます。正解は判明していません・・・
もやもやが漂い続ける結末となりました。
落ちのない記事で夏を涼しくお過ごしください🌻🍧✨
まえがき
この記事は、出典に記載の書籍に掲載された文章及びコードを引用し、適宜、掲載文章とコードを改変して書いています。
PyMC3 から PyMC Ver.5 への書き換えは「見つけることができた範囲内の処理内容」であり、処理の正確性は担保しておりません。
誤りや改善点がありましたら、ぜひ教えてください。
【出典】
「Pythonによるベイズ統計モデリング: PyMCでのデータ分析実践ガイド」(初版第1刷、Osvaldo Martin著、金子武久訳、翔泳社)
バージョンについて
PyMC 5.5.0 を利用しています。
記号について
コードのコメントに★印についている箇所が変更点です。
では、ベイズ統計と PyMC の旅へ進みましょう🚀
第5章 トレースオブジェクトとテンソル
PyMC3 の世界では、事後分布のサンプルデータは「トレースオブジェクト」と呼ばれています。
一方、PyMC Ver.5 は、公式サイトのサンプルコードを見る限り、「InferenceData」(推論データ?)と呼んでいるようです。
この記事では「トレースオブジェクト」の呼び方を使用します。
コード5.11
多重ロジスティック回帰モデル:データと境界決定を表示する
trace_1 データ、および、trace_1 データを extract(展開)して作成した trace_1_ext データの形状の把握に時間がかかりました。
# ★arvizのインポート
# import arviz as az
# ★extractデータの作成
trace_1_ext = az.extract(trace_1)
# 観測データX0を昇順ソートしてインデックス取得
idx = np.argsort(x_1[:, 0])
# ★観測データ点に対するbdの平均点の取得
# ld = chain_1['bd'].mean(0)[idx]
ld = trace_1_ext['bd'].mean(axis=1)[idx]
# 観測データの描画 見やすくする目的でcmapの値を変えています
plt.scatter(x_1[:, 0], x_1[:, 1], c=y_0, cmap='coolwarm')
# bdの平均線の描画
plt.plot(x_1[:, 0][idx], ld, color='r')
# ★bdのHDIの取得
# ld_hpd = pm.hpd(chain_1['bd'][idx]
ld_hdi = pm.hdi(trace_1.posterior, hdi_prob=0.95)['bd'][idx]
# bdのHDIの塗りつぶし
plt.fill_between(x_1[:, 0][idx], ld_hdi[:, 0], ld_hdi[:, 1], color='r',
alpha=0.5)
plt.xlabel(x_n[0], fontsize=16)
plt.ylabel(x_n[1], fontsize=16)
plt.show()【処理結果】
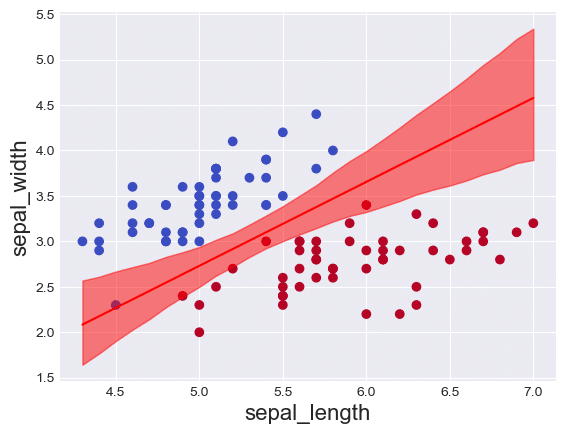
ほぼ正確にアヤメの分類ができています!
中央あたりでチューブが狭くなっている(不確実性が小さくなっている)様子が分かります。
8章の困難をイメージしやすくする目的で、このプロットの形状を覚えてくださいね。
コード5.16
ソフトマックス回帰モデル:パラメータのKDEとトレースを出力する(2)
softmax 関数を Theano から PyTensor へ変更するための調査に時間がかかりました。
# ★PyTensorのインポート
# import pytensor.tensor as pt
with pm.Model() as model_s:
# ★パラメータの事前分布 ~標準偏差の引数はsigmaです
alpha = pm.Normal('alpha', mu=0, sigma=2, shape=3)
beta = pm.Normal('beta', mu=0, sigma=2, shape=(4, 3))
# 線形予測子的なmu
mu = alpha + pm.math.dot(x_s, beta)
# ★パラメータθ:逆リンク関数的なソフトマックス関数
# theta = tt.nnet.softmax(mu)
theta = pt.special.softmax(mu, axis=-1)
# 尤度
yl = pm.Categorical('yl', p=theta, observed=y_s)
# ★パラメータの事後分布
# trace_s = pm.sample(2000, njobs=1)
trace_s = pm.sample(500, random_seed=1)
# ★トレースプロットの描画 plot_trace関数を利用
pm.plot_trace(trace_s, combined=True)
plt.tight_layout();【処理結果】
右側のトレースが激しくギザギザしていて(収束の徴候を示していて)、気持ちがいいです!

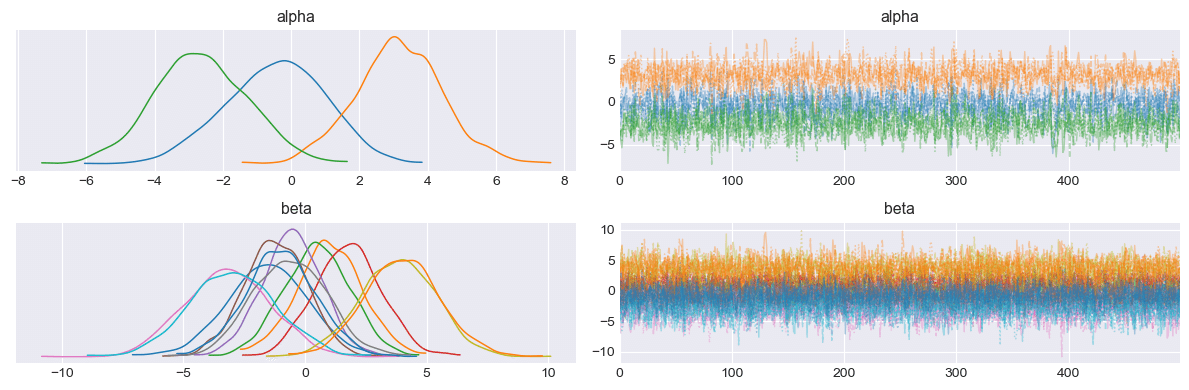
コード5.17
ソフトマックス回帰モデルでパラメータを固定化した場合のKDEとトレースを出力する(1)
trace_s データを extract して作成した trace_s_ext データの形状の把握に時間がかかりました。
行列&ベクトルの形状をうまく捕捉できず、ドット積(内積)の計算でエラーが出たり、理解不能な計算結果が現れたりと、大変でした(汗)
# ★extractデータの作成
trace_s_ext = az.extract(trace_s)
# ★150のデータ点に対応するyの予測値α+βXを計算
# data_pred = trace_s['alpha'].mean(axis=0) \
# + np.dot(x_s, trace_s['beta'].mean(axis=0)
data_pred = trace_s_ext['alpha'].mean(axis=1).data \
+ np.dot(x_s, trace_s_ext['beta'].mean(axis=2).data)
# softmax関数の計算ロジックで各クラスの所属確率を計算
y_pred = []
for point in data_pred:
y_pred.append(np.exp(point) / np.sum(np.exp(point), axis=0))
# np.argmax(y_pred, axis=1)で3クラスのうち最も確率が大きいクラスを選択
print('クラス所属確率の正解率')
np.sum(y_s == np.argmax(y_pred, axis=1)) / len(y_s)【処理結果】

コード5.18
ソフトマックス回帰モデルでパラメータを固定化した場合のKDEとトレースを出力する(2)
softmax 関数を Theano から PyTensor へ変更するための調査に時間がかかりました。
with pm.Model() as model_sf:
# ★パラメータの事前分布 ~標準偏差の引数はsigmaです
alpha = pm.Normal('alpha', mu=0, sigma=2, shape=2)
beta = pm.Normal('beta', mu=0, sigma=2, shape=(4, 2))
# ★theanoからPyTensorへの移行
# alpha_f = tt.concatenate([[0], alpha])
# beta_f = tt.concatenate([np.zeros((4, 1)), beta], axis=1)
alpha_f = pt.concatenate([[0], alpha])
beta_f = pt.concatenate([np.zeros((4, 1)), beta], axis=1)
mu = alpha_f + pm.math.dot(x_s, beta_f)
# ★theanoからPyTensorへの移行
# theta = tt.nnet.softmax(mu)
theta = pt.special.softmax(mu, axis=-1)
# 尤度
yl = pm.Categorical('yl', p=theta, observed=y_s)
# ★事後分布のサンプリング
# trace_sf = pm.sample(5000, njobs=1)
trace_sf = pm.sample(1250, random_seed=1)
# ★トレースプロットの描画 plot_trace関数を利用
pm.plot_trace(trace_sf, combined=True)
plt.tight_layout();【処理結果】
右下のカラフルなトレースが美しいです✨

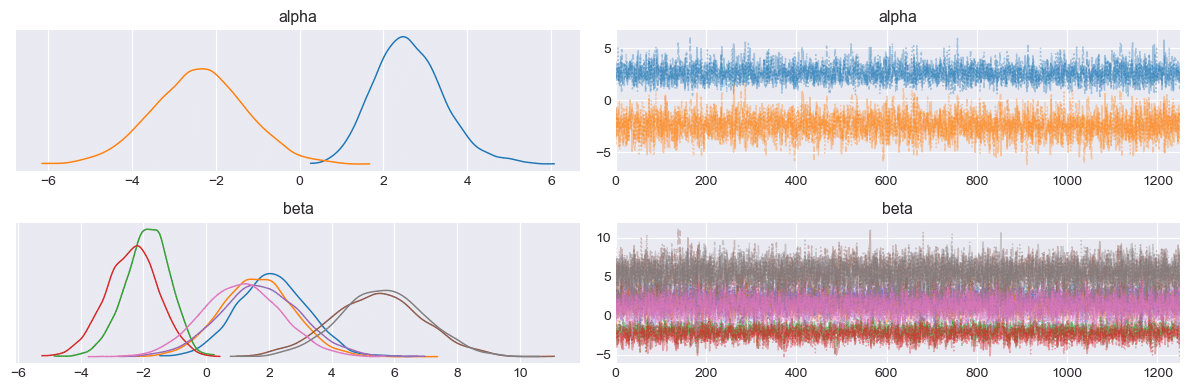
小まとめ
PyTensor のコード記法は Theano の記法を継承しているように感じました。
Model 定義に、ドット積(内積)とテンソルが絡んでくると、ドキドキしました。
第8章 ガウス過程のアウトプットが・・・
第8章「ガウス過程」はさまざまな意味で「不確実性」を孕む章でした。
ガウス過程を含むPyMCのモデルで予測した「具現化曲線」が、テキストのようにスッキリした曲線にならず、ばらけた糸片のような「不確実性だらけ」になってしまいました。
テキストの執筆時期にちょうど、PyMCはガウス過程モジュール(GPモジュール)を組み込んだようですが、テキストはGPモジュールを利用せず、ハンドメイドで実装しています。
PyMC Ver.5 には GPモジュールが組み込まれています。
このGPモジュールを使ってみては、と一瞬よぎった考え。
しかし、GPモジュールをどうやって使って良いのか、テキストの内容をGPモジュールにどのように変換できるのか、について、全くアイデアが得られず、GPモジュールの利用も断念しました。
GPの背中が遠い・・・
うまく結果が出なかった状況を共有いたします。
コード8.7
予め指定したハイパーパラメータでガウス過程のグラフを出力する
こちらのノイジーな線は、PyMC を利用しないで実装したコードによるものです。
テキストのような「滑らかな曲線」が生み出されず、「ノイズだらけの」グラフになってしまいました。
原因不明です(T_T)
【処理結果】
コード8.10~8.12
ガウス過程におけるハイパーパラメータをPyMC3で推論する
~
推定されたハイパーパラメータのもとでGP事後分布から具現化曲線を描く
このコードから、PyMC を利用してガウス過程を扱います。
まずは【モデルGP】についてです。
末尾のアウトプットは相当乱れています。
全体にわたって不確実性が大きくなっています。
原因不明です(T_T)
順を追って確認します。
① モデルの定義
Theano から PyTensor への書き換えがありましたが、テキストのコードから大きくずれる要因は無さそうです。
with pm.Model() as GP:
# パラメータの事前分布
mu = np.zeros(N)
eta = pm.HalfCauchy('eta', 5)
rho = pm.HalfCauchy('rho', 5)
sigma = pm.HalfCauchy('sigma', 5)
# 共分散行列 ★TheanoからPyTensorへ移行
D = squared_distance(x, x)
K = pt.fill_diagonal(eta * pm.math.exp(-rho * D), eta + sigma)
# 尤度
obs = pm.MvNormal('obs', mu, cov=K, observed=y)
# 事後予測密度
test_points = np.linspace(0, 10, 100)
D_pred = squared_distance(test_points, test_points)
D_off_diag = squared_distance(x, test_points)
k_oo = eta * pm.math.exp(-rho * D_pred)
K_o = eta * pm.math.exp(-rho * D_off_diag)
# パラメータの事後分布 ★TheanoからPyTensorへ移行
muPost = pm.Deterministic('muPost',
pm.math.dot(pm.math.dot(K_o, pt.nlinalg.matrix_inverse(K)), y))
SIGMApost = pm.Deterministic('SIGMApost',
K_oo - pm.math.dot(pm.math.dot(K_o, pt.nlinalg.matrix_inverse(K)),
K_o.T))② モデルの内容を確認
特段、おかしなところは無さそうです。
GP【処理結果】

pm.model_to_graphviz(GP)【処理結果】

③ 事後分布のサンプリング
テキストの乱数生成数 1000 に合わせて draws=250, chains=4 で実行しました。
with GP:
trace = pm.sample(250, random_seed=1)【処理結果】
「たった250サンプル」と指摘されます・・・ごめんね

④ プロットトレースの確認
テキストに近い形状でそこそこの結果が出ていると思います。
varnames = ['eta', 'rho', 'sigma']
pm.plot_trace(trace, combined=True, var_names=varnames)
plt.tight_layout();【処理結果】
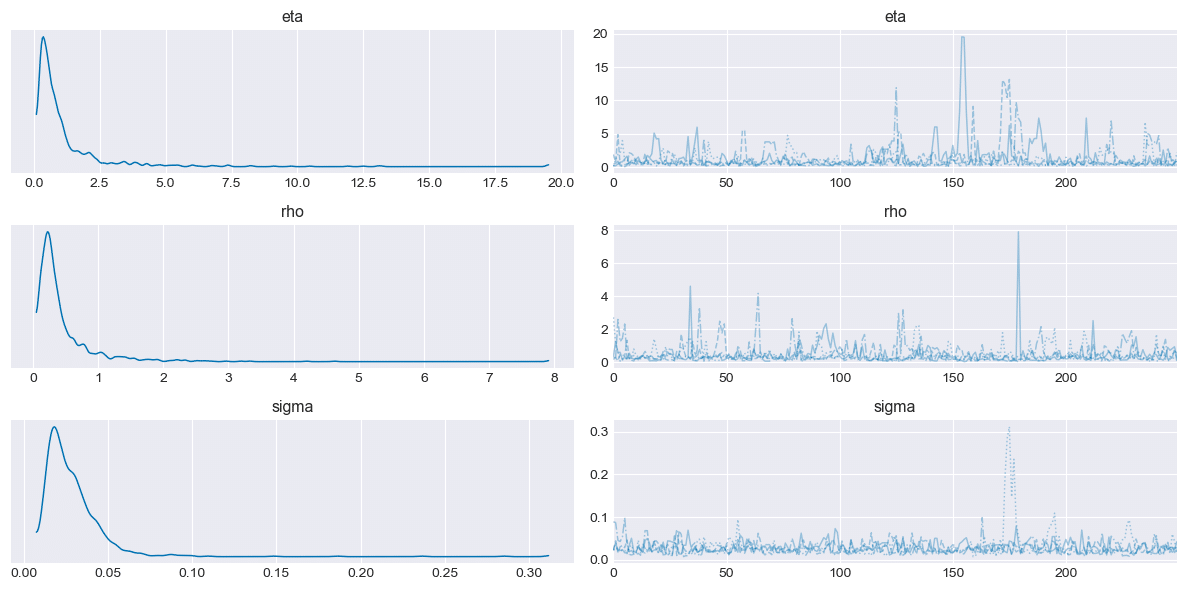
⑤ 要約統計量の確認
こちらもテキストの統計量と大きな乖離はないと思います。
pm.summary(trace, var_names=varnames)【処理結果】

⑥ GP事後分布から具現化曲線を描く
問題の処理です。
muPostとSIGMApostの形状変換を避けるべく、for文を用いたコードに書き換えました。
np.random.seed(1)
trace_ext = az.extract(trace)
skip = 5
for i in range(0, trace_ext.muPost.shape[1], skip):
m = trace_ext.muPost[:,i].data
S = trace_ext.SIGMApost[:,:,i].data
y_pred = np.random.multivariate_normal(m, S, check_valid='ignore')
plt.plot(test_points, y_pred, 'r-', alpha=0.1)
plt.plot(x, y, 'o')
plt.xlabel('$x$')
plt.ylabel('$f(x)$', rotation=0)
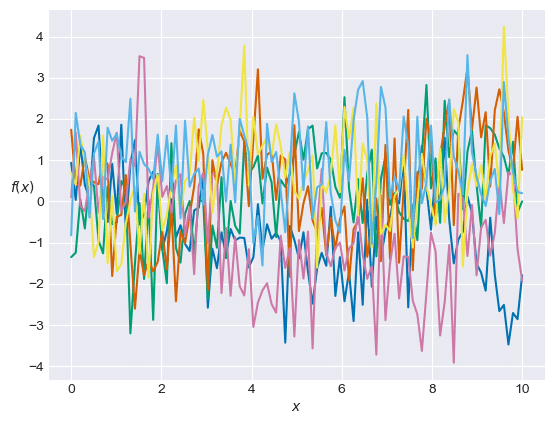
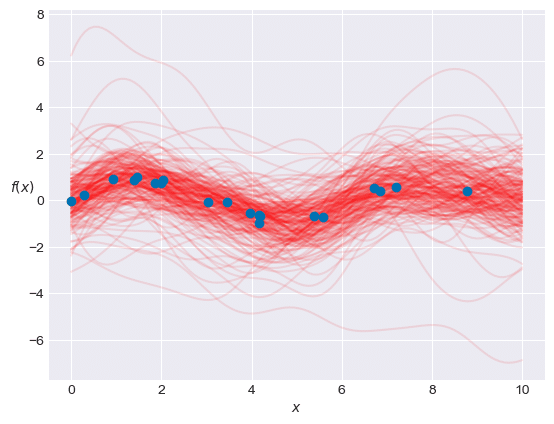
plt.show()【処理結果】
予測値 y_pred の値で描画した赤い線が、青いデータ点と乖離しています。
大きな不確実性を示しています。
縦軸の幅は、テキストは -2 ~ 2 程度ですが、このグラフは -6 ~ 8 です。
何がおかしいのやら・・・(謎)
同じような事象が次のモデルでも生じています。
コード8.13~8.14
周期カーネルを組み込んだGP事後分布から具現化曲線を描く(1)~(2)
データに周期性がある場合、周期性がある可能性が高い場合のモデルに、周期カーネルを取り入れます。
この周期カーネルを組み込んだガウス過程【モデルGP_periodic】も、末尾のグラフのとおり、事後分布の不確実性は高い状態になりました。
なぜでしょう・・・(謎)
① 周期関数の定義
periodic = lambda x, y: np.array([[np.sin((x[i] - y[j])/2)**2 \
for i in range(len(x))] for j in range(len(y))])② モデルの定義
以前のモデル【モデルGP】とよく似たモデルです。
with pm.Model() as GP_periodic:
# パラメータの事前分布
mu = np.zeros(N)
eta = pm.HalfCauchy('eta', 5)
rho = pm.HalfCauchy('rho', 5)
sigma = pm.HalfCauchy('sigma', 5)
# 共分散行列 ★TheanoからPyTensorへ移行
P = periodic(x, x)
K = pt.fill_diagonal(eta * pm.math.exp(-rho * P), eta + sigma)
# 尤度
obs = pm.MvNormal('obs', mu, cov=K, observed=y)
# 事後予測密度
test_points = np.linspace(0, 10, 100)
D_pred = periodic(test_points, test_points)
D_off_diag = periodic(x, test_points)
k_oo = eta * pm.math.exp(-rho * D_pred)
K_o = eta * pm.math.exp(-rho * D_off_diag)
# パラメータの事後分布 ★TheanoからPyTensorへ移行
muPost = pm.Deterministic('muPost',
pm.math.dot(pm.math.dot(K_o, pt.nlinalg.matrix_inverse(K)), y))
SIGMApost = pm.Deterministic('SIGMApost',
K_oo - pm.math.dot(pm.math.dot(K_o, pt.nlinalg.matrix_inverse(K)),
K_o.T))③ モデルの内容を確認
GP_periodic【処理結果】

pm.model_to_graphviz(GP_periodic)【処理結果】

④ 事後分布のサンプリング
テキストの乱数生成数 1000 に合わせて draws=250, chains=4 で実行しました。
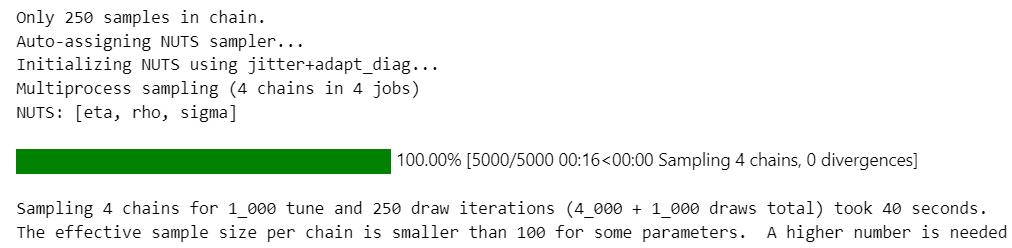
こちらのモデルでは、1chainあたりのサンプルサイズが小さいとのワーニングが出ています。
with GP_periodic:
trace = pm.sample(250)【処理結果】
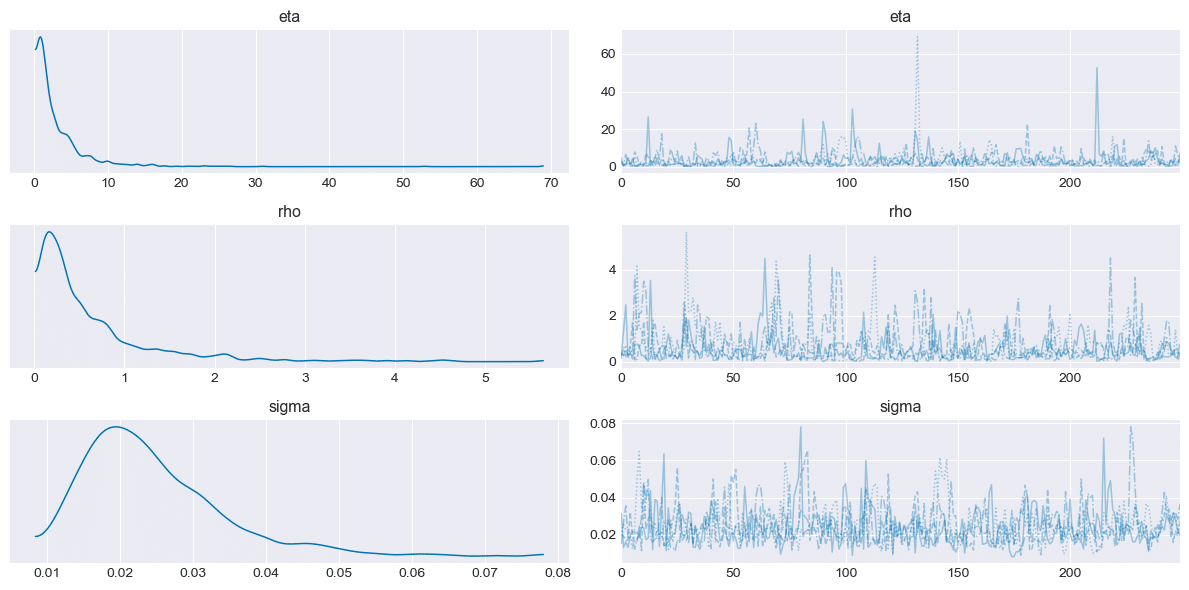
⑤ プロットトレースの確認
前のモデルと似たプロットになっていると思います。
varnames = ['eta', 'rho', 'sigma']
pm.plot_trace(trace, combined=True, var_names=varnames)
plt.tight_layout();【処理結果】
⑥ 要約統計量の確認
問題を見つけられません・・・
pm.summary(trace, var_names=varnames)【処理結果】

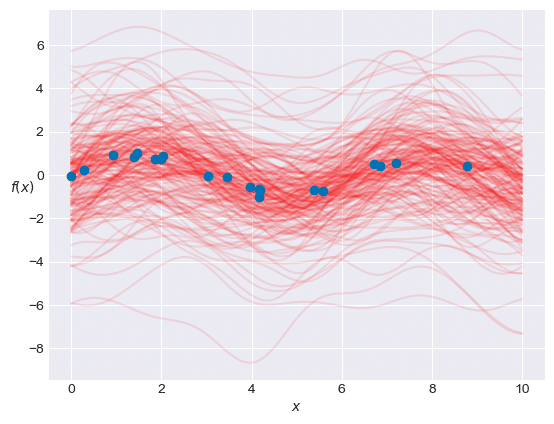
⑦ GP事後分布から具現化曲線を描く
ようこそ、不確実性の世界へ。
テキストのコードを書き換えています。
np.random.seed(1)
trace_ext = az.extract(trace)
skip = 5
for i in range(0, trace_ext.muPost.shape[1], skip):
m = trace_ext.muPost[:, i]
S = trace_ext.SIGMApost[:,:,i]
y_pred = np.random.multivariate_normal(m, S, check_valid='ignore')
plt.plot(test_points, y_pred, 'r-', alpha=0.1)
plt.plot(x, y, 'o')
plt.xlabel('$x$')
plt.ylabel('$f(x)$', rotation=0)
plt.show()【処理結果】
予測値 y_pred の値で描画した赤い線が、青いデータ点と「ますます」乖離しています。
テキストはどうやって不確実性を抑え込んだのでしょう・・・
知りたいです・・・
小まとめ
PyMC Ver.5 によるガウス過程の実装についてご存じの方、詳しく教えてください!!!
個人では解決不能です(T_T)
結び
PyMC3 から PyMC Ver.5 へ進む道はやはり険しいです。
PyMC Ver.5 ベースの書籍が出版されることを願ってやみません。
おわり
ブログの紹介
noteで3つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
2.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。
3.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
最後までお読みいただきまして、ありがとうございました。
