
「数値シミュレーションで読み解く統計のしくみ」をPythonで写経 ~ 第6章6.1「統計的検定とQRPs」
第6章「適切な検定のためのサンプルサイズ設計」
書籍の著者 小杉考司 先生、紀ノ定保礼 先生、清水裕士 先生
この記事は、テキスト「数値シミュレーションで読み解く統計のしくみ」第6章「適切な検定のためのサンプルサイズ設計」の6.1節「統計的検定とQRPs」の Python写経活動 を取り扱います。
第6章はシミュレーションを通じて、調査・実験の事前段階でサンプルサイズを設計する方法を学びます。
今回は問題のある研究実践(QRPs)を学びます。
R の基本的なプログラム記法はざっくり Python の記法と近いです。
コードの文字の細部をなぞって、R と Python の両方に接近してみましょう!
ではテキストを開いてシミュレーションの旅に出発です🚀
はじめに
テキスト「数値シミュレーションで読み解く統計のしくみ」のご紹介
このシリーズは書籍「数値シミュレーションで読み解く統計のしくみ〜Rでためしてわかる心理統計」(技術評論社、「テキスト」と呼びます)の Python写経です。
テキストは、2023年9月に発売され、副題「Rでためしてわかる心理統計」のとおり、統計処理に定評のある R の具体的なコードを用いて、心理統計の理解に役立つ数値シミュレーションを実践する素晴らしい書籍です。
引用表記
この記事は、出典に記載の書籍に掲載された文章及びコードを引用し、適宜、掲載文章とコードを改変して書いています。
【出典】
「数値シミュレーションで読み解く統計のしくみ〜Rでためしてわかる心理統計」初版第1刷、著者 小杉考司・紀ノ定保礼・清水裕士、技術評論社
記事中のイラストは、「かわいいフリー素材集いらすとや」さんのイラストをお借りしています。
ありがとうございます!
6.1 統計的検定とQRPs
QRPsは問題のある研究実践(questionable research practices)の略称です。
テキストによると…
・2010年代に心理学の実験結果が再現されない問題が話題となった
・中でも統計的検定が不適切に使われてきたことが指摘された
・現在は改革が進み、QRPsを避けるための枠組みが整理されてきた
テキストの統計的検定のデザインに関する説明がとてもわかり易いので引用させていただきます。
統計的検定は許容できるタイプⅠエラー確率($${\alpha}$$)とタイプⅡエラー確率($${\beta}$$)を定め、検定したい母数(パラメータ)・帰無仮説・対立仮説をあらかじめデザインすることが重要です。
検定前に決めておくべきことを以下に挙げます。
1.確率モデル、検定する母数
2.母数に関する帰無仮説
3.タイプⅠエラー確率($${\alpha}$$)とタイプⅡエラー確率($${\beta}$$)
4.検定統計量
5.サンプルサイズ
6.1節では2つの問題をシミュレーションで理解します。

この記事は Jupyter Notebook 形式(拡張子 .ipynb)でPythonコードを書きます。
概ね確率分布の特性値算出には scipy.stats を用い、乱数生成には numpy.random.generator を用いるようにしています。
主に利用するライブラリをインポートします。
### インポート
# 数値計算
import numpy as np
# 確率・統計
import scipy.stats as stats
import statsmodels.api as sm # 回帰分析等の統計処理
# 描画
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'Meiryo'
6.1.1 結果を見てから帰無仮説を変更する(HARKing)ことの問題
テキストによると HARKing とは…
一般に、結果を見てから仮説を変更することを Hypothesizing After the Results are Known の頭文字をとって、HARKing と呼びます。特に検定の文脈においては、検定結果を見てから帰無仮説を変更することを指します。
テキストは、HARKing の問題は検定の多重性に関わる問題を内在させている、としています。
この項では、HARKing によってタイプⅠエラー確率が上昇する問題が生じることを、統制群が1つ、実験群が2つの一元配置分散分析のシミュレーションで確認します。
具体的には以下のように検定を重ねます。
①分散分析が有意な場合はその旨を報告する
②有意でない場合はt検定を実施する
②-1 2つの群の1つ以上が有意な場合はその旨を報告する
②-2 2つの群の両方が有意でない場合は報告しない

■ HARKing でタイプⅠエラー確率が上昇することを確認するシミュレーション
群ごとに正規分布乱数を生成します。
有意水準$${5\%}$$で 10000 回のシミュレーションを実施します。
### 227ページ HARKingでタイプⅠエラー確率が上昇することを確認するシミュレーション
# 設定と準備
alpha = 0.05 # 有意水準
k = 3 # 群の数
n = [20, 20, 20] # 群ごとのサンプルサイズ
mu = [5, 5, 5] # 母平均(差は無い)
sigma = 2 # 母標準偏差(等分散を仮定)
iter = 10000 # シミュレーション回数
X = np.hstack([np.repeat(a=1, repeats=n[0]), # factor型ではない
np.repeat(a=2, repeats=n[1]),
np.repeat(a=3, repeats=n[2])])
# 結果を格納するオブジェクト
pvalue = np.zeros(iter)
type1_error = 0
# シミュレーション
rng = np.random.default_rng(seed=123)
for i in range(iter):
# 各グループのデータ(正規分布乱数)を生成してYに結合
Y1 = rng.normal(size=n[0], loc=mu[0], scale=sigma)
Y2 = rng.normal(size=n[1], loc=mu[1], scale=sigma)
Y3 = rng.normal(size=n[2], loc=mu[2], scale=sigma)
Y = np.hstack([Y1, Y2, Y3])
# 分散分析を実行、p値を取得
pvalue = sm.stats.anova_oneway(data=Y, groups=X, use_var='equal').pvalue
# HARKing
if pvalue < alpha: # 有意だった場合はその結果を報告する
type1_error += 1
else: # 有意にならなかった場合は対応のない2標本のt検定(Welch)を追加実施する
pvalue12 = stats.ttest_ind(Y1, Y2, equal_var=False).pvalue
pvalue13 = stats.ttest_ind(Y1, Y3, equal_var=False).pvalue
if (pvalue12 < alpha) | (pvalue13 < alpha):
type1_error += 1
# 結果
type1_error / iter【実行結果】
有意水準$${5\%}$$に対して、タイプⅠエラー確率は$${9.64\%}$$まで上昇しました。

テキストは、統計的検定の正当性は手続き全体が持つエラー確率をコントロールする点にあり、検定のための条件を事後に変更する・後知恵を働かせてしまわないよう、「事前登録」を行うことが推奨されている、としています。

6.1.2 サンプルサイズの事後決定
結果をみてからサンプルサイズを変更することも QRPs に該当するそうです。
このシミュレーションでは、有意になるまでサンプルサイズを大きくしてt検定を繰り返して、タイプⅠエラー確率を算出します。
■ ①事後にサンプルサイズを多くすることでタイプⅠエラー確率が上昇することを確認するシミュレーション1
20人を対象にした10回の実験をシミュレーションします。
有意水準$${5\%}$$で 10000 回のシミュレーションを実施します。サンプルサイズは10です。
有意にならないとき、サンプルサイズが20になるまでサンプルサイズを大きくします。
### 229ページ 2標本の母平均の差のstudent-t検定(等分散仮定)シミュレーション1
# 有意になるまでサンプルサイズを大きくする 1分10秒
# 設定と準備
n = [10, 10] # サンプルサイズ
mu = [0, 0] # 母平均が等しい設定にする
sigma = 2 # 母標準偏差
iter = 10000 # シミュレーション回数
alpha = 0.05 # 有意水準
# 結果を格納するオブジェクト
pvalue = np.zeros(iter)
# シミュレーション
rng = np.random.default_rng(seed=1)
for i in range(iter):
# 最初の実験
Y1 = rng.normal(size=n[0], loc=mu[0], scale=sigma) # 群1のデータ生成
Y2 = rng.normal(size=n[1], loc=mu[1], scale=sigma) # 群2のデータ生成
pvalue[i] = stats.ttest_ind(Y1, Y2, equal_var=True).pvalue # t検定のp値を取得
# p値がαより大きく、かつ、countが10未満のときに実験を反復(サンプルサイズを増す)
count = 0
while (pvalue[i] >= alpha) & (count < 10):
Y1 = np.append(Y1, rng.normal(size=1, loc=mu[0], scale=sigma))
Y2 = np.append(Y2, rng.normal(size=1, loc=mu[1], scale=sigma))
pvalue[i] = stats.ttest_ind(Y1, Y2, equal_var=True).pvalue # p値を追加取得
count += 1
## 結果
# 誤って帰無仮説を棄却した割合
type1_error = (pvalue < alpha).mean()
# 表示
print(type1_error)【実行結果】
有意水準$${5\%}$$に対して、タイプⅠエラー確率は$${13.26\%}$$まで上昇しました。

$${p}$$値が一様分布に従っているか確認します。
$${p}$$値のヒストグラムを描写する関数を定義します。
### p値のヒストグラム描画関数の定義
def plot_hist_pvalue(pvalue, bins=20):
# 描画領域の設定
plt.figure(figsize=(6, 3))
# ヒストグラムの描画
plt.hist(pvalue, bins=bins, ec='white', alpha=0.7)
# x軸ラベル、y軸ラベル、タイトルの設定
plt.xlabel('p value')
plt.ylabel('Frequency')
plt.title('Histogram of pvalue')
plt.show()$${p}$$値のヒストグラムを描写します。
### 230ページ 続き p値の分布 図6.1
plot_hist_pvalue(pvalue)【実行結果】
$${p}$$値が有意水準$${0.05}$$以下のときの頻度が異常に大きくなっています。
有意水準になるまでサンプルサイズを増やしたことが$${p}$$値を分布を歪めています。


■ ②事後にサンプルサイズを多くすることでタイプⅠエラー確率が上昇することを確認するシミュレーション2
こちらのシミュレーションは、$${p値}$$が$${10\%}$$以下の場合にサンプルサイズがを増やすものです(サンプルサイズの最大値は110)。
### 231ページ 2標本の母平均の差のstudent-t検定(等分散仮定)シミュレーション2
# p値が有意水準αの2倍(10%)の場合にサンプルサイズを大きくする
# 設定と準備
n = [10, 10] # サンプルサイズ
mu = [0, 0] # 母平均が等しい設定にする
sigma = 2 # 母標準偏差
iter = 10000 # シミュレーション回数
alpha = 0.05 # 有意水準
# 結果を格納するオブジェクト
pvalue = np.zeros(iter) # p値を格納する変数を宣言
# シミュレーション
rng = np.random.default_rng(seed=1)
for i in range(iter):
# 最初の実験
Y1 = rng.normal(size=n[0], loc=mu[0], scale=sigma) # 群1のデータ生成
Y2 = rng.normal(size=n[1], loc=mu[1], scale=sigma) # 群2のデータ生成
pvalue[i] = stats.ttest_ind(Y1, Y2, equal_var=True).pvalue # t検定のp値を取得
# p値がαの2倍に収まるとき、サンプルサイズを大きくしてp値を更新する(上限100回)
for j in range(100):
# 有意なときは実験を終了する
if pvalue[i] < alpha:
break
# p値がαの2倍に収まるとき、それぞれの条件で1回実験を追加する
elif pvalue[i] < alpha * 2:
Y1 = np.append(Y1, rng.normal(size=1, loc=mu[0], scale=sigma))
Y2 = np.append(Y2, rng.normal(size=1, loc=mu[1], scale=sigma))
# 新たにp値を取得
pvalue[i] = stats.ttest_ind(Y1, Y2, equal_var=True).pvalue
# αの2倍に収まらない場合はあきらめる
else:
break
## 結果
# 誤って帰無仮説を棄却した割合
type1_error = (pvalue < alpha).mean()
# 表示
print(type1_error)【実行結果】
シミュレーション1と比べて値は小さくなったものの、タイプⅠエラー確率は$${6.88\%}$$まで上昇しています。

$${p}$$値のヒストグラムを描写します。
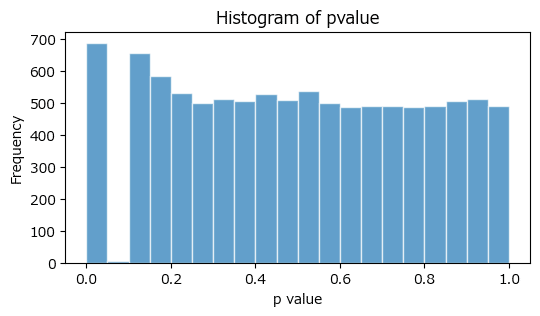
### 231ページ 続き p値の分布 232ページ図6.2
# p値が5~10%のとき追加実験をするので抜けてしまう
plot_hist_pvalue(pvalue)【実行結果】
$${p}$$値が$${5}$$~$${10\%}$$の区間が抜けています。
この区間に該当する場合、有意になるまでサンプルサイズを大きくしているからです。
今回の写経は以上です。
シリーズの記事
次の記事
前の記事
目次
ブログの紹介
note で7つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
Python、EXCELのサンプルコードの配布もあります。
2.実験!たのしいベイズモデリング1&2をPyMC Ver.5で
書籍「たのしいベイズモデリング」・「たのしいベイズモデリング2」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは R言語+Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう!
3.実験!岩波データサイエンス1のベイズモデリングをPyMC Ver.5で
書籍「実験!岩波データサイエンスvol.1」の4人のベイジアンによるベイズモデルを PyMC Ver.5で描いて分析します。
この書籍はベイズプログラミングのイロハをざっくりと学ぶことができる良書です。
楽しくPyMCモデルを動かして、ベイズと仲良しになれた気がします。
みなさんもぜひぜひPyMCで動かして、一緒に遊んで学びましょう!
4.楽しい写経 ベイズ・Python等
ベイズ、Python、その他の「書籍の写経活動」の成果をブログにします。
主にPythonへの翻訳に取り組んでいます。
写経に取り組むお仲間さんのサンプルコードになれば幸いです🍀
5.RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析をPythonとPyMC Ver.5 で実践します。
この書籍には時系列分析のテーマが盛りだくさん!
時系列分析の懐の深さを実感いたしました。
大好きなPythonで楽しく時系列分析を学びます。
6.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
統計・データサイエンス書籍にまつわる記事が多いです。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
7.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。
最後までお読みいただきまして、ありがとうございました。
