5-1 確率分布の定数の決定～ Google Colabで定積分して確率を求めよ！

ネイピア DS

2023年5月27日 12:22

今回の統計トピック

直線的な確率密度関数の定数計算に始まり、確率密度関数の可視化と確率の計算（積分計算）をPythonで「らくらく計算」します！
Google ColabでPythonをはじめますよ！

公式問題集の準備

「公式問題集」の問題を利用します。お手元に公式問題集をご用意ください。
公式問題集が無い場合もご安心ください！
「知る」「実践する」の章で、のんびり統計をお楽しみください！

問題を解く

📘公式問題集のカテゴリ

確率分布の分野
問1 確率分布の定数の決定（１か月の１人暮らしの水道使用量）

試験実施年月
統計検定2級 2019年11月問9（回答番号14）

問題

公式問題集をご参照ください。

解き方

題意
次の確率密度関数$${f(x)}$$の定数$${a\quad (a>0)}$$を求めます。

$$
f(x)=
\begin{cases}
a \left(1-\cfrac{x}{20} \right) & (0 \leq x \leq 20)\\
0 & (x<0, \quad x>20)
\end{cases}
$$

公式テキストより

ひとまず一般論から

連続型の確率分布
確率変数$${X}$$の値$${x}$$は連続値を取る「連続型」です。
連続型の確率変数$${X}$$と確率密度関数$${f(x)}$$の対応関係が連続型の確率分布です。
グラフにすると、横軸が確率変数$${X}$$、縦軸が$${X}$$に対応する確率密度関数$${f(x)}$$になります。

連続型確率分布の確率
連続型確率分布の確率は、確率密度関数のグラフの面積に相当します。
次の図の青塗りの部分は、確率変数$${X}$$が$${-2 \leq X \leq 2}$$の範囲を取る時の確率$${P(-2 \leq X \leq 2)}$$を示しています。

積分の記号を用いると$${a \leq X \leq b}$$の確率は次の式で計算できます。

$$
P(a \leq X \leq b) = \int^b_a f(x)dx
$$

また、全ての事象の確率の合計は 1 になるので、次の式が成り立ちます。

$$
P(\Omega)=\int^{\infty}_{-\infty} f(x)dx=1
$$

問題に戻ります。

解答の戦略
連続型確率分布の確率を「図形の面積で求める」か、「積分の計算で求めるか」、２つの解答戦略がありそうです。

１．図形の面積コース
問題文の式$${f(x)=a \left(1-\cfrac{x}{20} \right) \quad (0\leq x \leq 20)}$$の部分は「直線」っぽい感じがします。
$${0\leq x \leq 20}$$の範囲に関して、式を展開すると、$${f(x)=-\cfrac{a}{20}x +a}$$となり、切片$${a}$$、傾き$${-\cfrac{a}{20}}$$のグラフを書ける気がしてきました！
$${x<0, \quad x>20}$$の範囲は$${f(x)=0}$$であり、確率＝図形の面積には関係なさそうです。
ここまでの情報で、グラフ案を書いてみます。

三角形が見えてきました！

確率変数$${X=0}$$のとき$${f(x)=a}$$です。
確率変数$${X=20}$$のとき$${f(x)=0}$$です。
点$${(0,0)}$$、$${(0, a)}$$、$${{(20,0)}}$$を結ぶ三角形の面積を考えましょう。

三角形の面積は全事象の確率 1 です。
三角形の面積の公式に当てはめてみましょう。

$$
\begin{align*}
三角形の面積&=底辺 \times 高さ\div 2\\
1&=(20-0)\times(a-0)\div2\\
1&=20 \times a \div 2\\
1&=10a\\
10a&=1\\
a&=\cfrac{1}{10}
\end{align*}
$$

定数$${a=\cfrac{1}{10}}$$です。

定数$${a=\cfrac{1}{10}=0.1}$$を用いてグラフを最終化します。

水道使用量$${X}$$が多くなるにつれて、直線的に確率密度関数が小さくなっています。
水道使用量$${X=0}$$付近の確率密度関数が最大になっています。
これって、この町内には一定数（１割位？）の水道水をほとんど使わない１人暮らしの住人が住んでいる、ってことでしょうか！？
湧き水を利用しているのかしら？？？

２．積分コース

問題文の確率密度関数

$$
f(x)=
\begin{cases}
a \left(1-\cfrac{x}{20} \right) & (0 \leq x \leq 20)\\
0 & (x<0, \quad x>20)
\end{cases}
\tag{1.1}
$$

および、全事象の確率

$$
P(\Omega)=\int^{\infty}_{-\infty} f(x)dx=\int^{20}_{0} f(x)dx=1
\tag{1.2}
$$

より、$${0 \leq x \leq 20}$$の範囲に関して、式1.2の$${f(x)}$$に式1.1の$${f(x)}$$を代入して、次の式を導きます。

$$
\displaystyle \int^{20}_{0} a \left(1-\cfrac{x}{20} \right)dx=1
\tag{1.3}
$$

定積分の定数は外に出せるので（$${\int^b_a kf(x)dx = k \int^b_a f(x)dx}$$）、

$$
a \displaystyle \int^{20}_{0} \left(1-\cfrac{x}{20} \right)dx=1
\tag{1.4}
$$

定積分の計算をします。
$${F(x)}$$を微分すると$${f(x)}$$になるとき、$${\int^b_a f(x)dx=[F(x)]^b_a=F(b)-F(a)}$$より、

$$
\begin{align*}
a \left[x-\cfrac{x^2}{40} \right]^{20}_0&=1\\
\\
a \left(20-\cfrac{20^2}{40} \right)-a \left(0-\cfrac{0^2}{40} \right)&=1\\
\\
a \left(20-\cfrac{400}{40} \right)-a(0-0)&=1\\
\\
a(20-10)-0&=1\\
10a&=1\\
a&=\cfrac{1}{10}
\end{align*}
\tag{1.5}
$$

定数$${a=\cfrac{1}{10}}$$です。

定積分の計算の補足
$${F(x)}$$の微分が$${f(x)}$$になるとき、

$${f(x)=\left(1-\cfrac{x}{20} \right)}$$から$${F(x)}$$への操作は、

$${1 = 1 \times x^0 \rightarrow 1\times \cfrac{1}{1}x^1=x}$$
$${-\cfrac{x}{20} = -\cfrac{1}{20}x^1 \rightarrow -\cfrac{1}{20} \times\cfrac{1}{2}x^2= - \cfrac{1}{40}x^2=- \cfrac{x^2}{40}}$$

$${F(x)=x-\cfrac{x^2}{40}}$$になります。

すっきりして、いい（せ）気分です！

まとめ
連続型確率分布の確率密度関数$${f(x)}$$の積分＝面積が確率であること、そして、全事象の確率$${P(\Omega)=1}$$であることを手がかりにして、確率密度関数の定数を求めました。
今回の問題は確率密度関数が直線的なので、図形から面積を求める方法を使い勝手よく利用しました。
確率密度関数が複雑な形状の場合は、複雑な積分計算が必要になるかもです。

解答

④ です。

難易度　ふつう

・知識：連続型確率分布の確率密度関数、確率、積分
・計算力：数式組み立て（中）、数式計算（中）
・時間目安：2分

知る

おしながき

公式問題集の問題に接近してみましょう！
今回は、Pythonを用いて確率密度関数の確率を計算・可視化してまいりましょう！
パソコンでGoogle Colabにアクセスして、Pythonコードを動かします。

ちら見せ。こんな感じの可視化です。
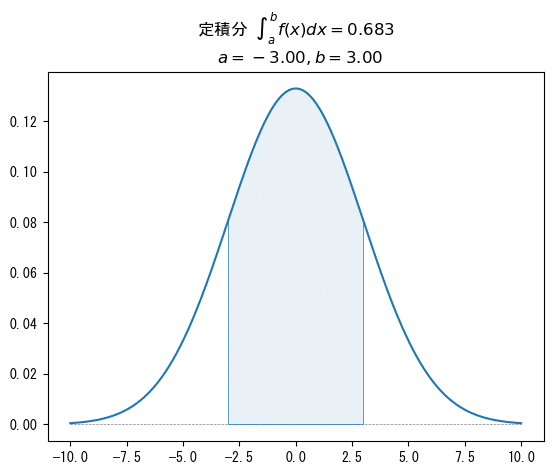
正規分布$${N(0, 3^3)}$$の確率密度関数です。
$${\pm1\sigma}$$の領域の面積＝確率は$${0.683}$$です。

「積分の計算はちょっと・・・」
大丈夫です。積分計算はパソコンが行います！
積分が難しくて確率密度関数の確率に触れないのはもったいないですよー！
確率密度関数のグラフを簡単に描画できるので、「見える化した確率」で確率密度関数のイメージが掴みやすくなると思います。

「いきなりPythonを動かすなんて・・・」
大丈夫です！サンプルプログラムを提供いたします！
ちょっとだけパソコンの操作を頑張れば、すぐに確率密度関数とお友達になれます（個人の見解です）。

Google Colabへ！

Google Colab（グーグルコラボ）はブラウザでPythonを動かすサービスです。

パソコンにPythonやライブラリをインストールする必要が無いので、気軽にPythonライフをスタートすることができます！

準備ステップ

１：Googleアカウントの取得とログイン
Google Colabを利用するには、Googleアカウントが必要です。
次のサイトなどを参考にして、Googleアカウントを取得しましょう。
その後、Googleにログインしましょう。

２：Google Colabにアクセス
このリンクよりGoogle Colabにアクセスします。https://colab.research.google.com/?hl=ja

Google Colab の準備ができたところで、いったん教室に戻ります。

連続型確率分布の確率密度関数

📕公式テキスト：2.4 確率変数と確率分布（64ページ～）

連続型確率分布の確率
確率変数$${X}$$が連続値のとき、確率は$${X}$$の１点で表現できません。
じつは連続型確率分布の確率は、確率密度関数のグラフの面積に相当するのです。
確率密度関数$${f(x)}$$の確率＝面積は積分$${\int f(x)dx}$$で表します。

図の青塗りの部分は、確率変数$${X}$$が$${-2 \leq X \leq 2}$$の範囲を取る時の確率$${P(-2 \leq X \leq 2)}$$を示しています。
積分を用いると次のように表すことができます。

$$
P(-2\leq X \leq 2)=\displaystyle \int^2_{-2}f(x)dx
$$

確率変数$${X}$$が区間$${[a, b]}$$を取るときの確率$${P}$$は、確率密度関数$${f(x)}$$を用いて次のように表します。

$$
P(a\leq X \leq b)=\displaystyle \int^b_a f(x)dx
$$

まとめます

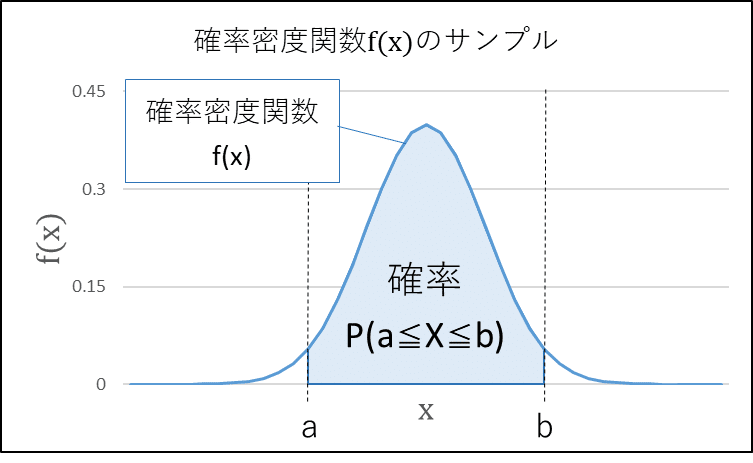
グラフの線＝確率密度関数$${f(x)}$$、確率変数$${X}$$の区間$${[a,b]}$$が定まると、確率$${P(a\leq X \leq b)}$$を計算できます。

この計算をPythonで実行しましょう！
$${f(x)}$$と$${[a,b]}$$を指定して、確率$${P(a\leq X \leq b)}$$の計算とグラフによる可視化を行います。
確率は定積分で計算します。

それでは、Google Colabに戻りましょう。

Pythonで確率計算

Pythonファイルのダウンロード
こちらのリンクからPythonファイルをダウンロードします。
Jupyter Notebook形式です。

Google Colabにアップロード
PythonファイルをGoogle Colabにアップロードします。
Google Colabのメニューを次のように選びます。

次の画面にPythonファイルをドラッグ・アンド・ドロップします。

この画面が表示されたらアップロード完了です。

確率計算の準備

さあ、最初のコードを動かします！
図のように▶をクリックして「インストール」の「pip ･･･」を実行します。
グラフに日本語を表示できるようになります。

同じように「インポート」を実行します。
確率計算などの「処理に必要なプログラムを使えるように準備する工程」です。

同じように「共通処理の定義」を実行します。
この部分には「確率の計算＝定積分の計算」と「グラフの描画」の処理のプログラムを書いています。

このコードを少し解説いたします。

■定積分の計算

Pythonの科学技術計算用のライブラリ scipy の「quad」という１変数関数の積分計算プログラムを利用しています。
【使い方】
quad( 関数f(x), 区間の下限 a, 区間の条件 b )
【注意事項】
quadの計算結果は「近似値」です。

確率計算の実行

公式問題集で出題された確率密度関数を試してみましょう！

グラフを表示しました。

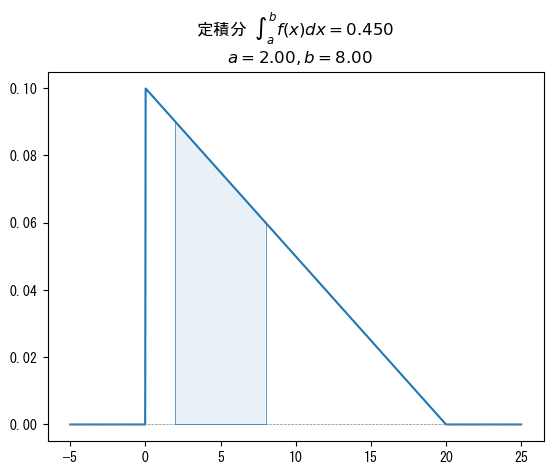
上部の「定積分」のところに計算結果を表示しています。
区間$${[2, 8]}$$の確率$${P(2\leq X \leq 8)}$$は$${0.45}$$です。
青塗りの部分は区間$${[2, 8]}$$の確率$${P(2\leq X \leq 8)}$$＝面積の領域です。
グラフの青い線は区間$${[-5,25]}$$の範囲で確率密度関数$${f(x)}$$を表示しています。

解説します。

■確率密度関数$${f(x)}$$の定義
確率密度関数を設定しています。
この部分にさまざまな確率密度関数を設定することで、さまざまな確率計算を行うことができます。

■関数の描画区間の設定
確率密度関数$${f(x)}$$のグラフの線を表示する区間$${[\mathrm{x\_min}, \mathrm{x\_max}]}$$を設定します。
この例では$${[-5, 25]}$$を設定しています。

■定積分の積分区間の設定
確率密度関数$${f(x)}$$の確率$${P(a\leq X \leq b)}$$を求める区間$${[a, b]}$$を設定します。
この例では$${[2, 8]}$$を設定しています。

設定を変えてみましょう。

関数の描画区間を$${[-10, 30]}$$、定積分の積分区間を$${[0, 20]}$$に変更して、▶をクリックして、コードを実行しましょう。

確率は 1 です。

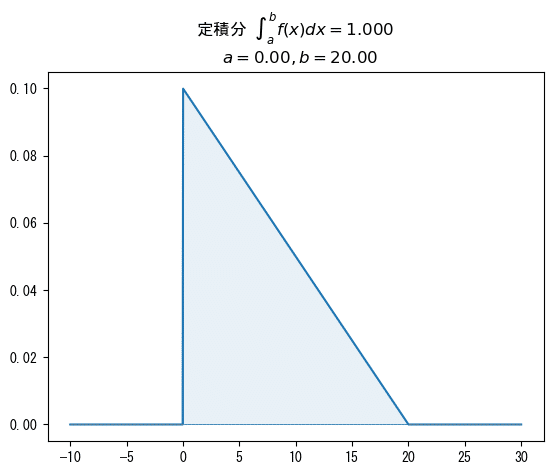
関数の描画区間を$${[-10, 30]}$$、定積分の積分区間を$${[5, 15]}$$に変更して、▶をクリックして、コードを実行しましょう。

確率は 0.5 です。

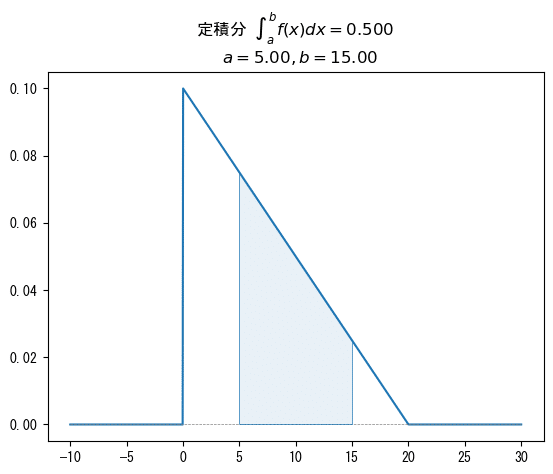
このように、２つの区間を変えてみて、確率密度関数の確率のイメージをどんどん膨らませてみてくださいね。

さまざまな確率密度関数の可視化

Pythonファイルのいくつかの確率密度関数のグラフを例示いたします。
▶をクリックして、どんどん実行してください！

【例４】

$$
f(x)=
\begin{cases}
3x &(0\leq x\leq2/3)\\
-6x+6 &(2/3< x\leq1)\\
0 &(x<0, 1<x)\\
\end{cases}
$$

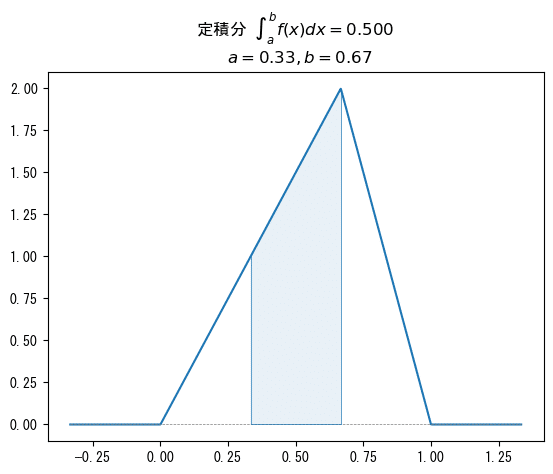
【例７】

$$
f(x)=
\begin{cases}
-\cfrac{3}{500}x^2 + \cfrac{3}{50}x &(0\leq x\leq1)\\
0 &(x<0, 1<x)\\
\end{cases}
$$

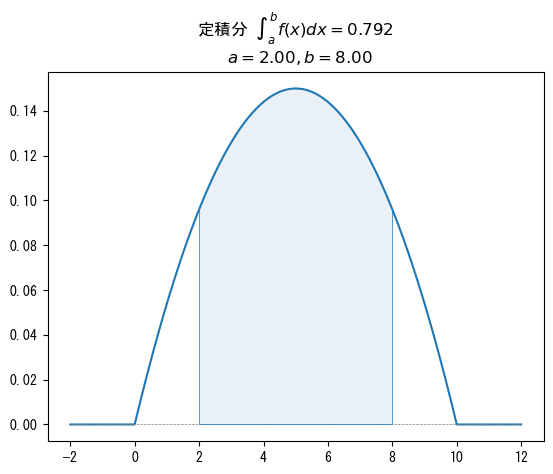
実は一般の関数にも使えます
このPythonファイルは確率密度関数に加えて、一般の１変数関数に用いることができます。
たとえば多項式はこんな感じ。

$$
f(x)=x-\cfrac{x^3}{5}+\cfrac{x^5}{99}-\cfrac{x^7}{7150}
$$

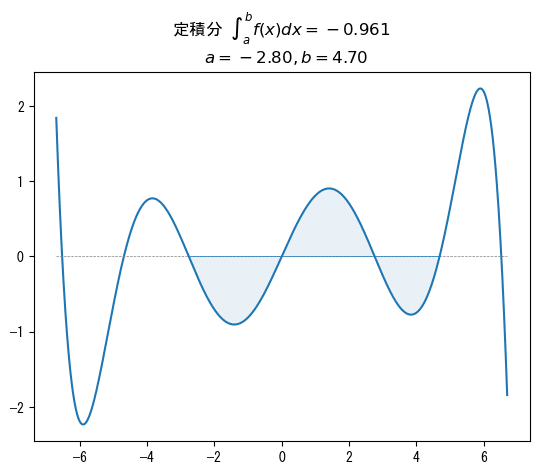
過学習の匂いがいたします・・・。

Pythonファイルの全貌は「Pythonで作成してみよう！」の項で紹介いたします。

Pythonファイルの保存
確率密度関数の設定をいろいろ変えて、結果を保存したい時がありますよね！
Google ColabのPythonファイルをパソコンのローカルフォルダに保存する方法をお知らせします。

Google Colabのメニューを選んで、Pythonファイルをローカルドライブにします。

再度、Google ColabでPythonファイルを実行したいときには、ローカルドライブに保存したPythonファイルをGoogle Colabのメニュー「ファイル＞ノートブックをアップロード」してください。

実践する

Pythonを用いて確率密度関数の確率を計算・可視化みよう！

「知る」で解説した一連の「Pythonを用いて確率密度関数の確率を計算・可視化」を実践しましょう！

電卓・手作業で作成してみよう！

今回はお休みです。

EXCELで作成してみよう！

今回はお休みです。

EXCELサンプルファイルのダウンロード
今回はファイル提供はありません。

Pythonで作成してみよう！

プログラムコードを読んで、データを流したりデータを変えてみたりして、データを追いかけることで、作表ロジックを把握する方法も効果的でしょう。
サンプルコードを揃えておけば、類似する作表作業を自動化して素早く結果を得ることができます。

今回は、確率密度関数の確率計算と可視化に取り組みます。
「知る」のお題を動かしてみましょう！

①インストール
グラフに日本語フォントを表示するライブラリをインストールします。

!pip install japanize-matplotlib

②インポート
scipy.integrateのquadで１次元の積分計算（数値積分）を行います。

import numpy as np
from scipy.integrate import quad
from scipy.stats import norm
import matplotlib.pyplot as plt
import japanize_matplotlib

③共通処理の定義
積分計算とグラフ表示の共通処理をPython関数で定義します。

# xの型に応じて関数case_f(x)の処理を変える
def f(x):
    if isinstance(x, (int, float)): # xがint型、float型の場合、map処理が不要
        fx = def_f(x)
    else:
        fx = list(map(lambda z: def_f(z), x))
    return fx

#  積分計算、関数・積分区分のプロット
def f_plot(x_min=0, x_max=1, a=None, b=None):
    japanize_matplotlib.japanize()
    if a is None:
        a = x_min
    if b is None:
        b = x_max

    # 関数の値の取得
    x = np.linspace(x_min, x_max, 1000)  # 変数 X の値を取得
    y = f(x)                             # 関数f(x)の値を取得

    # 積分区間[a,b]の定積分計算
    result = quad(f, a, b, limit=1000) 

    # 関数の描画
    plt.plot(x, y)

    # 積分区間[a,b]の領域の描画
    y0 = 0                               # y=0
    x_ab = np.linspace(a, b, 1000)       # 積分区間[a,b]の変数Xの値を取得
    y_ab = f(x_ab)                       # 積分区間[a,b]の関数f(x)の値を取得
    plt.fill_between(x_ab, y_ab, y0,     # 面を塗りつぶす描画
                     alpha=0.1) 
    plt.hlines(y0, x_min, x_max, lw=0.5, # y=0の水平線の描画 x_min≦X≦x_max
               color='gray', ls='--')
    plt.hlines(y0, a, b, lw=0.5)         # y=0の水平線の描画 a≦X≦b
    plt.vlines(a, y0, y_ab[0], lw=0.5)   # x=aの垂直線の描画
    plt.vlines(b, y0, y_ab[-1], lw=0.5)  # x=bの垂直線の描画

    plt.title(f'定積分 $\int^b_a f(x)dx={result[0]:.3f}$\n $a={a:.2f}, b={b:.2f}$')
    plt.show()
    return result

④さまざまな確率密度関数の定積分・プロット処理の実行

■公式問題集の問題の確率密度関数

$$
f(x)=
\begin{cases}
-\cfrac{1}{200}x+\cfrac{1}{10} &(0\leq x \leq 20)\\
0 &(x<0, x>20)\\
\end{cases}
$$

# 確率密度関数：f(x)=-1/200x+1/20 (0≦x≦20), f(x)=0 (other)

# 【設定】確率密度関数f(x)の定義
def def_f(x, **kwargs):
    if x < 0:
        fx = 0
    elif x <= 20:
        fx = -x/200 + 1/10
    elif x > 20:
        fx = 0
    return fx 

# 【設定】関数f(x)の描画区間[x_min,x_max]
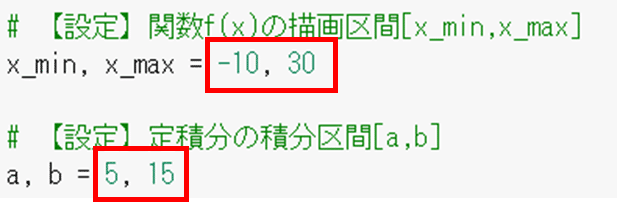
x_min, x_max = -10, 30

# 【設定】定積分の積分区間[a,b]
a, b = 5, 15

# 処理の実行
integrate_result = f_plot(x_min, x_max, a, b)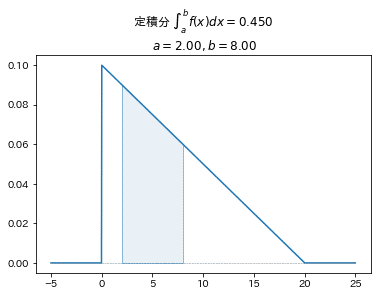

■確率密度関数例1

$$
f(x)=
\begin{cases}
0.1 &(0\leq x\leq10)\\
0 &(x<0, 10<x)\\
\end{cases}
$$

# 確率密度関数：f(x)=1/10 (0≦x≦10), f(x)=0 (other)

# 【設定】確率密度関数f(x)の定義
def def_f(x, **kwargs):
    if x < 0:
        fx = 0
    elif x <= 10:
        fx = 0.1
    elif x > 10:
        fx = 0
    return fx 

# 【設定】関数f(x)の描画区間[x_min,x_max]
x_min, x_max = -5, 15

# 【設定】定積分の積分区間[a,b]
a, b = 2, 8

# 処理の実行
integrate_result = f_plot(x_min, x_max, a, b)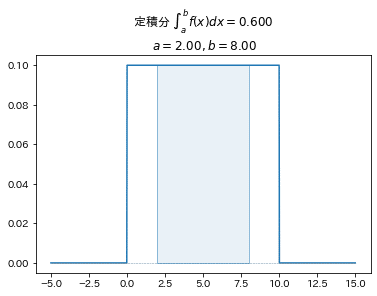

■確率密度関数例2

$$
f(x)=
\begin{cases}
x/6 &(0\leq x<2)\\
1/3 &(2\leq x\leq4)\\
0 &(x<0, 4<x)\\
\end{cases}
$$

# 確率密度関数：f(x)=x/6 (0≦x＜2), f(x)=1/3 (2≦x≦4),  f(x)=0 (other)

# 【設定】確率密度関数f(x)の定義
def def_f(x, **kwargs):       
    if x < 0:
        fx = 0
    elif x < 2: 
        fx = x/6
    elif x <= 4:
        fx = 1/3
    else:
        fx = 0
    return fx 

# 【設定】関数f(x)の描画区間[x_min,x_max]
x_min, x_max = -1, 5

# 【設定】定積分の積分区間[a,b]
a, b = 1, 3

# 処理の実行
integrate_result = f_plot(x_min, x_max, a, b)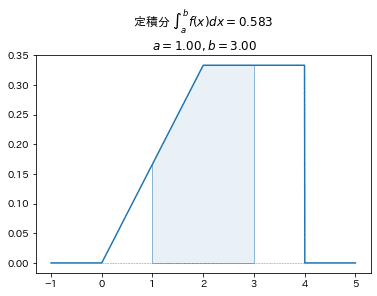

■確率密度関数例3

$$
f(x)=
\begin{cases}
x+1 &(-1\leq x\leq0)\\
-x+1 &(0\leq x\leq1)\\
0 &(x<-1, 1<x)\\
\end{cases}
$$

# 確率密度関数：f(x)=x+1 (-1≦x≦0), f(x)=-x+1 (0≦x≦1), f(x)=0 (other)

# 【設定】確率密度関数f(x)の定義
def def_f(x, **kwargs):
    if x < -1:
        fx = 0
    elif x <= 0:
        fx = x + 1
    elif x <= 1:
        fx = -x + 1
    elif x > 1:
        fx = 0
    return fx 

# 【設定】関数f(x)の描画区間[x_min,x_max]
x_min, x_max = -1.5, 1.5

# 【設定】定積分の積分区間[a,b]
a, b = -0.5, 0.5

# 処理の実行
integrate_result = f_plot(x_min, x_max, a, b)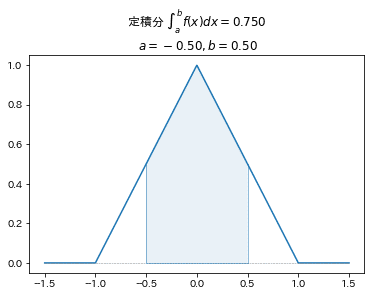

■確率密度関数例4

$$
f(x)=
\begin{cases}
3x &(0\leq x\leq2/3)\\
-6x+6 &(2/3< x\leq1)\\
0 &(x<0, 1<x)\\
\end{cases}
$$

# 確率密度関数：f(x)=3x (0≦x≦2/3), f(x)=-6x+6 (2/3＜x≦1), f(x)=0 (other)

# 【設定】確率密度関数f(x)の定義
def def_f(x, **kwargs):
    if x < 0:
        fx = 0
    elif x <= 2/3:
        fx = 3*x
    elif x <=1 :
        fx = -6*x + 6
    elif x > 1:
        fx = 0
    return fx 

# 【設定】関数f(x)の描画区間[x_min,x_max]
x_min, x_max = -1/3, 4/3

# 【設定】定積分の積分区間[a,b]
a, b = 1/3, 2/3

# 処理の実行
integrate_result = f_plot(x_min, x_max, a, b)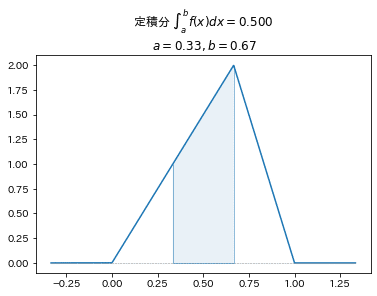

■確率密度関数例5

$$
f(x)=
\begin{cases}
-6x^2+6x &(0\leq x\leq1)\\
0 &(x<0, 1<x)\\
\end{cases}
$$

# 確率密度関数：f(x)=-6x^2 + 6x (0≦x≦1), f(x)=0 (other)

# 【設定】確率密度関数f(x)の定義
def def_f(x, **kwargs):
    if x < 0:
        fx = 0
    elif x <= 1:
        fx = -6*x**2 + 6*x
    elif x > 1:
        fx = 0
    return fx 

# 【設定】関数f(x)の描画区間[x_min,x_max]
x_min, x_max = -0.25, 1.25

# 【設定】定積分の積分区間[a,b]
a, b = 0.1, 0.9

# 処理の実行
integrate_result = f_plot(x_min, x_max, a, b)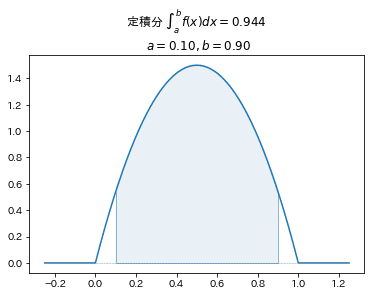

■確率密度関数例6

$$
f(x)=
\begin{cases}
-0.75x^2+1.5x &(0\leq x\leq2)\\
0 &(x<0, 2<x)\\
\end{cases}
$$

# 確率密度関数：f(x)=-0.75x^2 + 1.5x (0≦x≦2), f(x)=0 (other)

# 【設定】確率密度関数f(x)の定義
def def_f(x, **kwargs):
    if x < 0:
        fx = 0
    elif x <= 2:
        fx = -0.75*x**2 + 1.5*x 
    elif x >  2:
        fx = 0
    return fx 

# 【設定】関数f(x)の描画区間[x_min,x_max]
x_min, x_max = -0.5, 2.5

# 【設定】定積分の積分区間[a,b]
a, b = 0.5, 1.5

# 処理の実行
integrate_result = f_plot(x_min, x_max, a, b)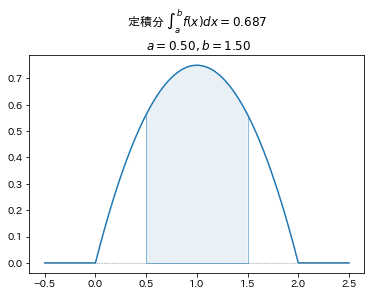

■確率密度関数例7

$$
f(x)=
\begin{cases}
-\cfrac{3}{500}x^2 + \cfrac{3}{50}x &(0\leq x\leq10)\\
0 &(x<0, 10<x)\\
\end{cases}
$$

# 確率密度関数：f(x)=-3/500x^2 + 3/50x (0≦x≦10), f(x)=0 (other)

# 【設定】確率密度関数f(x)の定義
def def_f(x, **kwargs):
    if x < 0:
        fx = 0
    elif x <= 10:
        fx = -3/500*x**2 + 3/50*x
    elif x > 10:
        fx = 0
    return fx 

# 【設定】関数f(x)の描画区間[x_min,x_max]
x_min, x_max = -2, 12

# 【設定】定積分の積分区間[a,b]
a, b = 2, 8

# 処理の実行
integrate_result = f_plot(x_min, x_max, a, b)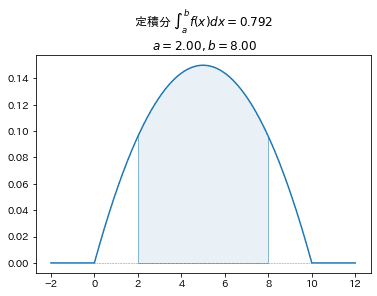

■確率密度関数例8　正規分布 $${N(0, 3^2)}$$
正規分布のパラメータ「平均$${\mu}$$」と「標準偏差$${\sigma}$$」は、def_f関数内のmuに平均、stddevに標準偏差を設定します。

# 確率密度関数：f(x)=正規分布(平均=0, 標準偏差=3)

# 【設定】確率密度関数f(x)の定義
def def_f(x, **kwargs):
    mu = 0      # 平均
    stddev = 3  # 標準偏差
    fx = norm.pdf(x, loc=mu, scale=stddev)
    return fx 

# 【設定】関数f(x)の描画区間[x_min,x_max]
x_min, x_max = -10, 10

# 【設定】定積分の積分区間[a,b]
a, b = -3, 3         # 1σ
# a, b = -np.inf, np.inf  # -∞～∞：塗りつぶしがうまく動作しない

# 処理の実行
integrate_result = f_plot(x_min, x_max, a, b)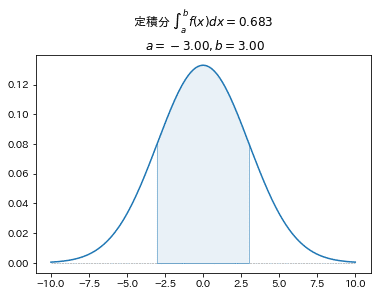

無限大$${(-\infty, \infty)}$$は「np.inf」で指定します。
ただし、グラフの塗りつぶしはうまく動作しません。

⑤一般の関数

■関数例1 三角関数

$$
f(x)=\sin(2x)
$$

# 関数：f(x)=sin(2x)

# 【設定】関数f(x)の定義
def def_f(x, **kwargs):
    fx = np.sin(2*x)
    return fx 

# 【設定】関数f(x)の描画区間[x_min,x_max]
x_min, x_max = -5*np.pi, 5*np.pi

# 【設定】定積分の積分区間[a,b]
a, b = -2*np.pi, 1.5*np.pi

# 処理の実行
integrate_result = f_plot(x_min, x_max, a, b)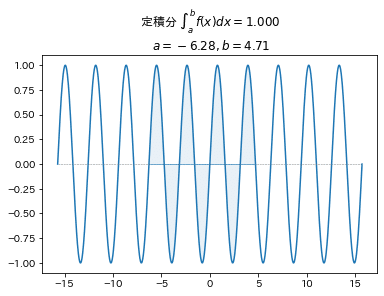

■関数例2 三角関数

$$
f(x)=\sin(0.01x^3)+0.1x
$$

# 関数：f(x)=sin(0.01x^3)+0.1x

# 【設定】関数f(x)の定義
def def_f(x, **kwargs):
    fx = np.sin(0.01*x**3) + 0.1*x
    return fx 

# 【設定】関数f(x)の描画区間[x_min,x_max]
x_min, x_max = -5*np.pi, 5*np.pi

# 【設定】定積分の積分区間[a,b]
a, b = 2.6*np.pi, 5*np.pi

# 処理の実行
integrate_result = f_plot(x_min, x_max, a, b)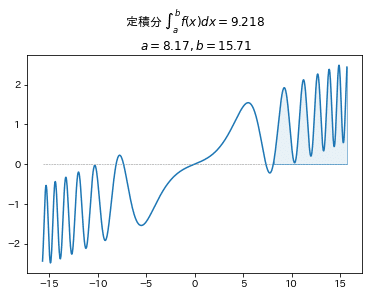

■関数例3 多項式

$$
f(x)=x-\cfrac{x^3}{5}+\cfrac{x^5}{99}-\cfrac{x^7}{7150}
$$

# 関数：f(x)= x - 1/5x^3 + 1/99x^5 - 1/7150x^7

# 【設定】関数f(x)の定義
def def_f(x, **kwargs):
    fx = x - x**3/5 + x**5/99 - x**7/7150
    return fx 

# 【設定】関数f(x)の描画区間[x_min,x_max]
x_min, x_max = -6.7, 6.7

# 【設定】定積分の積分区間[a,b]
a, b = -2.8, 4.7

# 処理の実行
integrate_result = f_plot(x_min, x_max, a, b)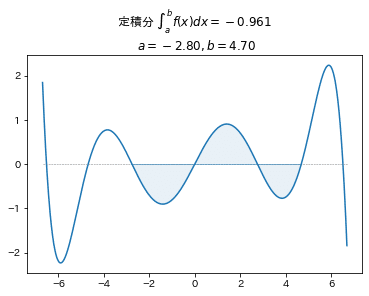

■関数例4 xの分数（x=0の取り扱いに注意）

$$
f(x)=
\begin{cases}
f(x)=\cfrac{1}{100x} & (x\neq0)\\
0 &(x=0)\\
\end{cases}
$$

# 関数：f(x)=1/(100x) (x≠0), f(x)=0 (x＝0)

# 【設定】関数f(x)の定義
def def_f(x, **kwargs):
    if x == 0:
        fx = 0
    else:
        fx = 1/(100*x)
    return fx 

# 【設定】関数f(x)の描画区間[x_min,x_max]
x_min, x_max = -0.1, 0.1

# 【設定】定積分の積分区間[a,b]の下端aと上端b
a, b = 0.01, 0.1

# 処理の実行
integrate_result = f_plot(x_min, x_max, a, b)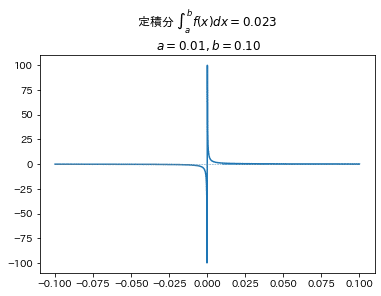

【留意事項：ゼロ除算】
ゼロ除算（0で割ること）が発生すると積分計算ができません。
上記処理ではひとまず、$${x=0}$$のときに$${f(x)=0}$$になるように、関数f(x)の定義を設定しています。
また、グラフでは開区間の制御を行っていないので、$${x=0}$$のときに$${f(x)=0}$$をプロットしています。

Pythonサンプルファイルのダウンロード
「知る」の章にてPythonサンプルファイルをダウンロードしてください。

積分の記事のご紹介

Pythonのパッケージ「SymPy」を利用した積分の実践記事を紹介いたします。
SymPyはひとことで言うと「Pythonで動く高性能電卓」。
積分、微分、行列等の計算を行ってくれます。
次の２つの記事では、SymPyで定積分と微分を実践しています。

次のサイトでSymPyの使い方を学ぶことができます。

おわりに

今回はPythonコードの実施を前面に出してみました。
統計学では積分計算が必要な場面が多々あるようです。
もちろん、積分をサクサク計算できるに越したことはありません。
しかし、積分のハードルがそれなりに高いことも事実です。

今回の試みは、積分計算を省略しつつ、確率密度関数の確率を感覚的に受け入れられることを狙っています。
Pythonのハードルがあります。
なんとかPython（というよりもGoogle Colab）のハードルを下げて、「区間の値を変更して確率が変わることを、グラフや面積の値の変化で感覚的に体験できる」ように、頑張ってみました。

そんな私もscipyの積分計算（integrate）とmatplotlibの塗りつぶし（fill_between）は、記事を書き始める２日前に知ったばかり。
知ったばかりの知ったかぶりでスミマセン（ペコリ）。
※そして、執筆当時は未だsympyの存在を知る由もなかったのです・・・

最後までお読みいただきまして、ありがとうございました。

のんびり統計シリーズの記事

次の記事

前の記事