実験！たのしいベイズモデリング１＆２をPyMC Ver.5 で【まえがき】

ネイピア DS

2023年10月14日 01:07

この記事は「シリーズのまえがき」と「PyMCを動かすまでの準備」の２点に焦点をあてています。
「PyMCを動かすまでの準備」には Google Colaboratory でPyMCベイズ推論を実行する簡単なサンプルコードを掲載しています。

まえがき

シリーズ：実験！「たのしいベイズモデリング１＆２」をPyMC Ver.5で

本シリーズは２つの書籍（北大路書房、以下「テキスト」と呼びます）を PyMC Ver.5 で実践した軌跡の記録です。

たのしいベイズモデリング: 事例で拓く研究のフロンティア
たのしいベイズモデリング2: 事例で拓く研究のフロンティア

「with pm.Model() as model:」に記述したPyMCモデルがきっかけとなって、ブログをお読みいただいた皆さんがテキストのベイズモデリングをお楽しみいただけたなら、この上ない幸せです🌹

テキスト「たのしいベイズモデリング」の紹介

テキストは、2018年9月に初版発行され、心理学研究のデータ分析をR言語とStanによるベイズモデリングで実践する素晴らしい書籍です。
目次（テーマ）を見ただけでワクワクしました！
第１章なんて「ピー」的なアレです！
下記 amazonサイトで目次をご堪能くださいませ。

楽しそうなテーマが満載で、きっとPyMCのモデリングはたのしいだろう、きっとテーマ・事例を通してベイズモデリングの学びが心地よく進むだろうと、とっても期待して書籍を購入しました。

そしてそして、まえがきもカッコいいのです！
編者の豊田秀樹先生はまえがきで、ベイズモデリングを「尤度を使って現象を考える心理学研究のパラダイムである」とし、次のように説明しています。

「この興味深い現象は、どのように生成され、データとして自分の眼前に現れたのだろう」という疑問に尤度を使って答えることである。確率分布によってデータの生成過程をモデル化することである。

テキスト「まえがき」より引用

テキスト「たのしいベイズモデリング２」の紹介

テキストは、2019年11月に初版発行され、前編に引き続き、心理学研究のデータ分析をR言語とStanによるベイズモデリングで実践する素晴らしい書籍です。
前編から１年程度が過ぎ、ベイズモデリングが活躍するシチュエーション、バリエーション、ステージが多様化して、テキストの全19章が取り上げるテーマも高度化・洗練化されています。

前編によるベイズモデリングが病みつきになり、すぐに「２」を入手しました。
最初の章は「チョコボールのエンゼルが当たる確率」。
とても興味をそそる魅惑のテーマです。
PyMCモデリングが成功するといいのですが・・・。

Stan から PyMC の変換はハードルが高かった

ベイズモデリングの界隈は「R言語＋Stan」勢力が強い所感です。
Python＋PyMCでベイズを学んできた私は、やはりPyMCでベイズモデリングの学びを継続したく、R+StanからPyMCへのコード変換を通じてベイズモデリングを学ぶ道に挑戦しました。
実践途中で気がついたのが「Stanのモデル表現はとても柔軟性が高いこと」です。
私のスキル不足が主因でしょうけど、PyMCに変換できない・しずらい・分からないモデルがテキストに満載なのです！

したがって、今回のPyMC化作業で「完全に変換できたモデル」はそう多くはありません。
そこで、以下のような状況を暗中模索で実践し、間違いや出来なかったことを含めて、ブログに記録することにしました。

・事後分布からのサンプリングデータがテキストと異なる
・テキストと異なるモデルで代替する
・収束が悪い（$${\hat{R}}$$値が高い）
・エラーが発生して棄権
・モデル自体の難易度が高すぎて、端からPyMC化を棄権

困難だらけでしたが、作成したPyMCモデルがエラー無く動いて、しかもテキストの意図どおりの結果を得られたとき、得も言われぬ感動・快感に満たされました！

引用掲示

このシリーズの記事は、出典に記載の書籍に掲載された文章及びコードを引用し、適宜、掲載文章とコードを改変して書いています。
PyMC Ver.5 のコードは「見つけることができた範囲内の処理内容」であり、処理の正確性は担保しておりません。
誤りや改善点がありましたら、ぜひ教えてください。

【出典】
１．「たのしいベイズモデリング: 事例で拓く研究のフロンティア」（初版第３刷、豊田秀樹編、北大路書房）
２．「たのしいベイズモデリング2: 事例で拓く研究のフロンティア」（初版第２刷、豊田秀樹編、北大路書房）

PyMC を動かすまでの準備

Anacondaでパソコンに環境構築するケースと、パソコンにインストール不要のWebサービス「Google Colaboratory」を利用するケースに関する参考情報です。
記事では、Anaconda に PyMC 専用環境を構築し、VSCodeでJupyter notebook 形式のコードを書いて、実行しています。

Anaconda環境構築の例

AnacondaでPyMC環境を構築
主役ライブラリの「pymc」は numpy等の別パッケージとの強いバージョン依存関係があるようですので、PyMC専用の環境をAnacondaで構築することをおすすめします。

numpyroをPyMC環境へ
記事ではNUTSサンプリングの時間短縮の目的で「numpyro」を利用します。
PyMC標準のNUTSサンプラーでは何時間もかかるモデルがあり、ここはひとつ、高速サンプラーを導入しましょう。
numpyroもnumpy等とのバージョン依存関係あるようですので、PyMC環境へ特別にインストールします。

以降では、インストール済みのAnacondaを利用して、PyMC環境を構築する手順の概要を説明いたします。

①インストールしながらPyMC環境作成
PyMC公式サイトのcondaインストール方法に準拠して実行します。
conda-forgeからpymc、bambi、seaborn、ipykernelを一気にインストールしてPyMC環境を新規作成します。
環境名の部分は、pymc_envなどの環境名を設定してください。

conda create -c conda-forge -n pymc_env 環境名 bambi seaborn ipykernel

②PyMC環境へ移動
PyMC環境をアクティブにします。

conda activate 環境名

③numpyroのインストール
condaでは何故か整合性エラーが発生してインストールできなかったので、やむを得ずpipでインストールしました。

pip install numpyro

④tensorflow-probabilityのインストール
tensorflow-probabilityはnumpyroが参照するライブラリですので、合わせてインストールします。
こちらも pip で。

pip install tensorflow-probability

（参考）記事作成に用いたPyMC環境の主要ライブラリ等のバージョン

python                    3.11.6  # Python本体

pymc                      5.9.0   # PyMC
pytensor                  2.17.1  # PyMCの裏で動く強者・テンソル計算
arviz                     0.16.1  # PyMCの統計量計算・描画を担当
bambi                     0.12.0  # GLM等をformula文で記述

numpyro                   0.13.2  # 高速NUTSサンプラーとして活用
jax                       0.4.18  # numpyroの裏で動く強者
tensorflow-probability    0.22.0  # numpyroが参照する働き者

numpy                     1.25.2
pandas                    2.1.1
matplotlib-base           3.8.0
seaborn                   0.13.0
graphviz                  8.1.0   # modelの描画で活躍
python-graphviz           0.20.1  # modelの描画で活躍

Google Colaboratory利用の例

Google Colaboratory はネット上でPythonを実行できる Google のサービスです。
パソコンに Python をインストールする必要がないので、手軽に Python を始めることができます。
もちろん、Google Colaboratory で PyMC を動かすことができます。

■ PyMCのインストールと簡単な動作確認
Google Colaboratory の Notebook 上で PyMC をインストールします。

# pymcのインストール
!pip install pymc

【実行結果】
Chrome ブラウザではこんな感じに見えます。

パッケージをインポートしてバージョンを表示します。

# インポート
import pymc as pm
import pandas as pd
# バージョン情報の表示
print('pymc:', pm.__version__)

【実行結果】2024年1月9日現在

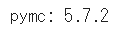
シンプルなお試しデータを作成します。

# データの作成
data = pd.DataFrame({'x': [1, 3],'y': [5, 8]})
display(data)

【実行結果】

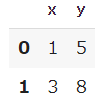
ここからは、PyMCを用いたお試しデータのベイズ推論実行に移ります。
PyMCでシンプルなモデルを定義してMCMCを実行します。
$${y = a + bx}$$で表現できる線形回帰モデルに誤差相当の標準偏差$${s}$$を加味したスチューデントの$${t}$$分布を尤度に指定しています

## モデルの定義とMCMCの実行
with pm.Model() as model_pm:
    # 事前分布の設定
    a = pm.Uniform('a', lower=0, upper=10)
    b = pm.Uniform('b', lower=0, upper=10)
    s = pm.HalfCauchy('s', beta=15)
    # 尤度の設定
    y = pm.StudentT('y', nu=5, mu=a + b * data.x, sigma=s, observed=data.y)
    # MCMCの実行：事後分布からのサンプリング
    idata_pm = pm.sample(random_seed=123)

【実行結果】

MCMCで得たパラメータの事後分布サンプリングデータを確認します。

## 事後分布の確認
# 事後分布サンプリングデータの要約統計量
display(pm.summary(idata_pm))
# トレースプロットの表示
pm.plot_trace(idata_pm, backend_kwargs={'constrained_layout': True});

【実行結果】
$${\hat{R} \leq 1.01}$$であり、また、トレースプロットの右側グラフの乱雑な様子から、収束していると判断しましょう。

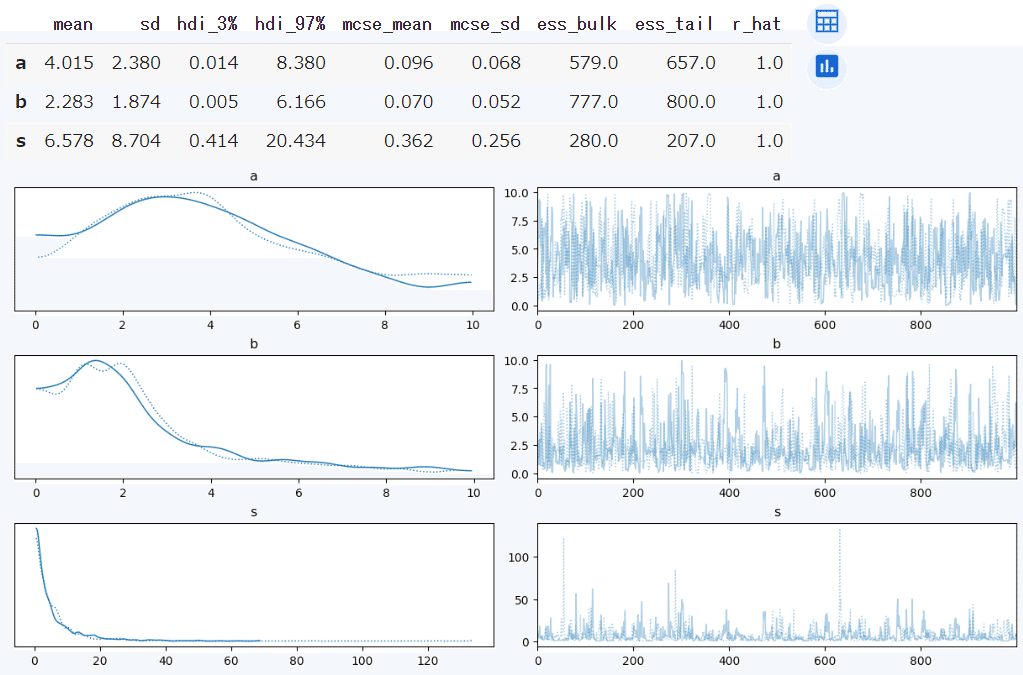
パラメータ事後分布を可視化します。

## 事後分布プロットの描画
pm.plot_posterior(idata_pm);

【実行結果】

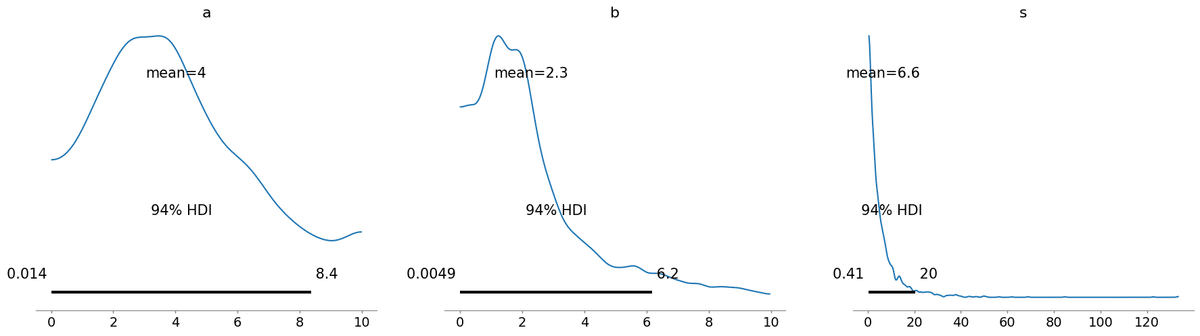
■ Bambiのインストールと簡単な動作確認
Bambiのインストールと同時にPyMCがインストールされます。

# bambiのインストール
!pip install bambi

パッケージをインポートしてバージョンを表示します。

# インポート
import bambi as bmb
import pymc as pm
import pandas as pd
# バージョン情報の表示
print('bambi:', bmb.__version__)

【実行結果】2024年1月9日現在

シンプルなお試しデータを作成します。PyMCのケースと同じデータです。

# データの作成
data = pd.DataFrame({'x': [1, 3],'y': [5, 8]})
display(data)

【実行結果】

ここからは、Bambi＆PyMCを用いたお試しデータのベイズ推論実行に移ります。
Bambiでシンプルなモデルを定義してMCMCを実行します。
$${y = 切片 + 傾き \times x}$$で表現できる線形回帰モデルに誤差相当の標準偏差$${sigma}$$を加味した正規分布を尤度に指定しています。
あわせて、MCMCで得たパラメータの事後分布サンプリングデータを確認します。

# モデルの定義
model_bmb = bmb.Model(formula='y ~ x', data=data)
# モデルの表示
print(model_bmb)
# MCMCの実行：事後分布からのサンプリング
idata_bmb = model_bmb.fit(random_seed=123, target_accept=0.9995)
# 事後分布サンプリングデータの要約統計量
display(pm.summary(idata_bmb))
# トレースプロットの表示
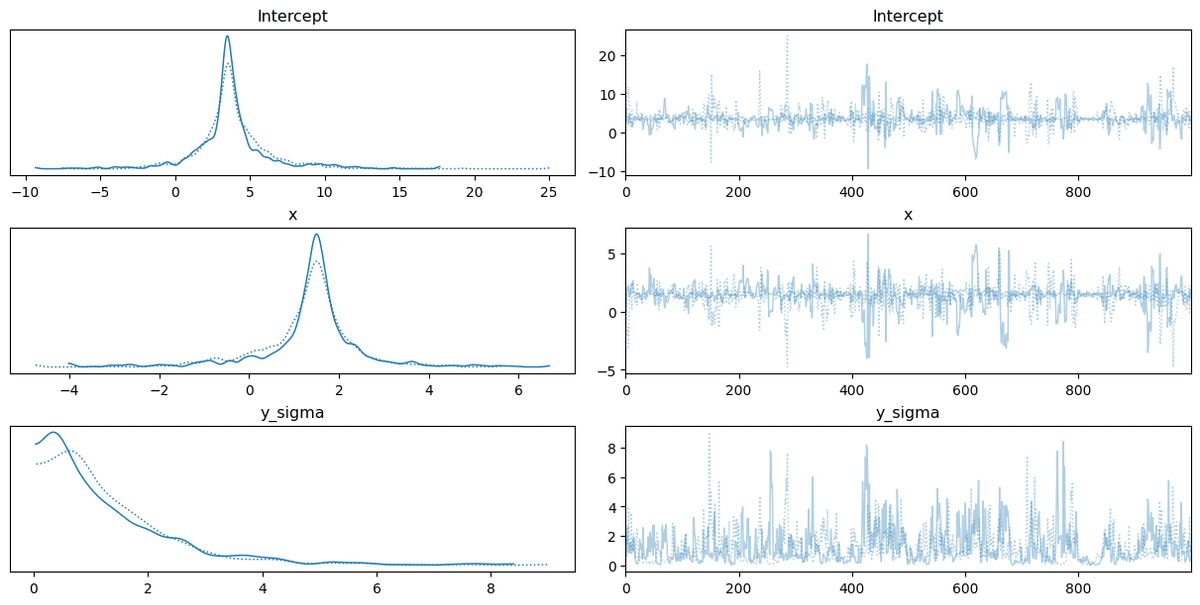
pm.plot_trace(idata_bmb, backend_kwargs={'constrained_layout': True});

【実行結果】
$${\hat{R} \leq 1.01}$$であり、また、トレースプロットの右側グラフの乱雑っぽい様子から、収束していると判断しましょう。

パラメータの事後分布を可視化します。

## 事後分布プロットの描画
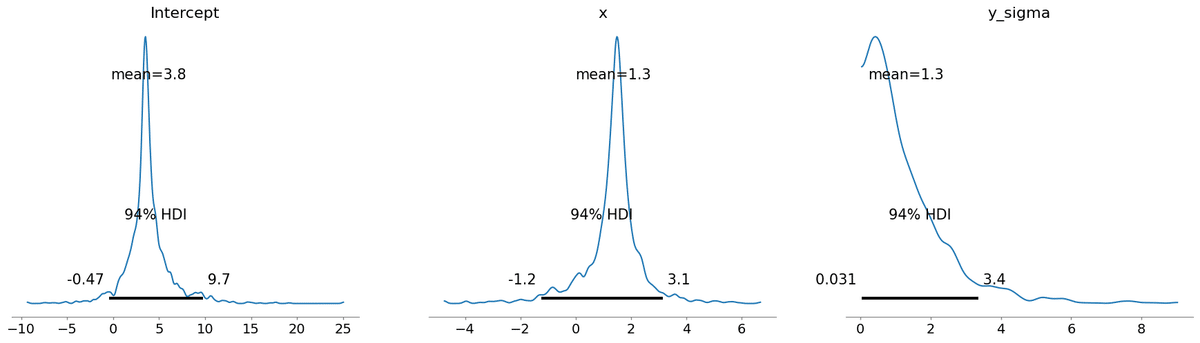
pm.plot_posterior(idata_bmb);

【実行結果】
Intercept：切片、x：説明変数 x の傾き、y_sigma：目的変数が従う正規分布の標準偏差の３つのパラメータについて、事後分布サンプリングデータの分布の形状を見ることができます。

インストール＆コード紹介は以上で完了です。

（注）Google Colaboratory と numpyro
numpyroは Google Colaboratory でインストール可能ですが、MCMC実行時にエラー発生する場合があります。

以上でこの記事は終了です。

シリーズの記事

ブログの紹介

note で４つのシリーズ記事を書いています。
ぜひ覗いていってくださいね！

１．のんびり統計
統計検定２級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定２級公式問題集CBT対応版に対応しています。

２．RとStanではじめる心理学のための時系列分析入門を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析トピックを PythonとPyMC Ver.5で取り組みます。
豊富なテーマ（お題）を実践することによって、PythonとPyMCの基礎体力づくりにつながる、そう信じています。
日々、Web検索に勤しみ、時系列モデルの理解、Pythonパッケージの把握、R・Stanコードの翻訳に励んでいます！
このシリーズがPython時系列分析の入門者の参考になれば幸いです🍀

３．Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learn と PyTorch の教科書です。
よかったらぜひ、お試しくださいませ。

４．データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Python のコラムを不定期に綴っています。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
ベイズ書籍の実践記録も掲載中です。

最後までお読みいただきまして、ありがとうございました。

この記事が気に入ったらサポートをしてみませんか？