第２章「血液型と性格には関連がある？」のベイズモデリングをPyMC Ver.5 で

2023年10月23日 17:52

この記事は、テキスト「たのしいベイズモデリング」の第２章「血液型と性格には関連がある？」のベイズモデルを用いて、PyMC Ver.5で「実験的」に実装する様子を描いた統計ドキュメンタリーです。

今回は初学者に優しい入門編的なモデルです。
果たして血液型と性格には関連があるのでしょうか？
PyMCでモデリングして、ベイズ推論を楽しみましょう！

テキストの紹介、引用表記、シリーズまえがき、PyMC等のバージョン情報は、このリンクの記事をご参照ください。

テキストで使用するデータは、R・Stan等のサンプルスクリプトとともに、出版社サイトからダウンロードして取得できます。

サマリー

テキストの概要

執筆者　　　：　下司忠大先生
モデル難易度：　★・・・・　（やさしい）

自己評価

評点

$$
\begin{array}{c:c:c}
実装精度 & ★★★★★& GoooD!\\
結果再現度 & ★★★★・& あと１歩\\
楽しさ & ★★★★★ & 楽しい！ \\
\end{array}
$$

評価ポイント

「血液型と性格の関係」という興味津々のデータ分析なので、モデリングから結果の分析まで楽しく取り組めました。
テキストにモデルの数式が詳しく掲載されているので、容易にPyMCのモデリングができました。
テキストの推定値と結果が異なっていますが、原因が分からず悩んでいます。

工夫・喜び・反省

「たのしいベイズモデリング」の実践で初めて納得できるPyMCモデルになりました。（第１章がラスボスだったこともあり）

モデルの概要

テキストの調査・実験の概要

血液型と性格の間に統計学的に有意な関連を示した論文（Tsuchimine, Saruwatari, Kaneda, & Yasui-Furukori (2015)）のデータを用いて、血液型による性格「持続」の差が実質的に意味のある差かどうかをベイズ推論で調べます。

【ちょっぴり補足】
元となった論文では、「持続」の性格について、Ａ型は他の血液型に比べて平均値が有意に高かった、としているそうです。
これはざっくり「A型は他の血液型に比べて持続的な性格である」ということのようです。
経験的で何となくのイメージですが、A型は我慢強さがありそうなので、持続の性格が強い印象があります（あくまで個人の感想です）。

テキストの調査概要に戻ります。
性格「持続」に関する質問数が８つあり、はいの回答が１点、いいえの回答が０点でカウントされ、データには、回答者（データ１行）ごとに血液型と得点（満点８）が記録されています。
８つの質問の内容はテキストに掲載されています。
また、こちらの論文のpdfファイルからも確認できます。

テキストのモデリング

目的変数$${y_{ji}}$$は「持続」の得点であり、独立に正規分布に従うと仮定しています。
正規分布のパラメータは、平均$${\mu_j}$$が血液型ごとの平均、標準偏差が$${\sigma_e}$$です。
関心があるパラメータは、この血液型ごとの平均パラメータ$${\mu_i}$$です。

$$
y_{ji} \sim \text{Normal}(\mu_j,\ \sigma_e) \\
\mu_{j} \sim \text{Uniform}(0, 100) \\
\sigma_e \sim \text{Uniform}(0, 100) \\
$$

テキストより一部改変して引用

添字$${j}$$は水準のラベルであり、血液型$${\{A, B, O, AB\}}$$です。
添字$${i}$$は血液型ごとのデータ番号です。
例えばＡ型の5番目の得点は$${y_{A5}}$$です。

パラメータ$${\mu_{j},\ \sigma_e}$$の事前分布は十分に広い範囲の一様分布を仮定しています。

■分析・分析結果
「持続」の性格について、Ａ型とＯ型、Ａ型とＡＢ型で差があるかどうかを、事後分布からサンプリングした平均パラメータ$${\boldsymbol{\mu_i}}$$～血液型別の持続得点の平均データを用いて分析します。
効果量$${\delta}$$、非重複度$${U_3}$$、優越率$${\pi_d}$$という概念が出現します！

分析結果はテキストに記載のとおりです。
PyMCモデリングでの分析結果は、「PyMC実装」章の【分析】の部分をご覧ください。

PyMC実装

Let's enjoy PyMC & Python !

準備・データ確認

１．インポート

### インポート

# ユーティリティ
import pickle

# 数値・確率計算
import pandas as pd
import numpy as np
import scipy.stats as stats

# PyMC
import pymc as pm
import pytensor.tensor as pt
import arviz as az

# 描画
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'

# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')

２．データの読み込み
csvファイルをpandasのデータフレームに読み込みます。

### データの読み込み
data = pd.read_csv('Blood.csv')
# カラム名を読み替え
data.columns = ['血液型', '血液型コード', '新奇性追求', '損害回避', '報酬依存',
                '持続', '自己志向', '協調', '自己超越']
display(data)

【実行結果】
血液型ごとに、「新奇性追求」から「自己超越」までの７つの性格得点が記録されています。
このモデリングでは性格「持続」の得点を目的変数に用いて、血液型との関係を調べます。

３．データの外観・統計量（テキストの表2.1、表2.2に対応）
まず、血液型ごとのデータ数を確認します。

### 血液型ごとの人数のカウント
count_data = data['血液型'].value_counts().to_frame()
count_data['比率'] = count_data['count'] / count_data['count'].sum()
display(count_data.round(2))

【実行結果】
血液型ごとのデータ数の比率は、ほぼ４：３：２：１です。

要約統計量を確認しましょう。テキストの表2.1を代替します。

### 記述統計量の表示　★表2.1に対応
data.iloc[:, 2:].describe().T.round(2)

【実行結果】
性格ごとの質問数は、新奇性追求40、損害回避35、報酬依存32、持続8、自己志向44、協調42、自己超越33です。
「持続」は最小得点0から最大得点8まで幅広い区間があります。
ちなみに「報酬依存」の最大値22は質問数32からかなり乖離しているようです。
また「自己超越」には欠損値がありますが、「持続」の分析に影響しないので、削除や加工をしないで、そのまま置いておきます。

血液型ごとの性格別得点を確認しましょう。テキストの表2.2を代替します。

### 血液型別の性格得点 ★表2.2に対応
data.groupby(['血液型'])[data.columns[2:]].agg(['mean', 'std']).T.round(2)

【実行結果】
みなさんが想像する血液型と性格の関係と比べて、この数値はいかがでしょう？

性格「持続」の血液型別ヒストグラムを確認しましょう。

### 性格「持続」の血液型別ヒストグラムの描画
sns.histplot(data=data, x='持続', hue='血液型', bins=9, stat='density',
             common_norm=True, element='step')
plt.title('「持続」の血液型別得点のヒストグラム')
plt.xlabel('得点')
plt.ylabel('確率密度');

【実行結果】
血液型ごとに差があるのか無いのか、よく分かりません・・・。

モデル構築

モデルの数式表現
目指したいPyMCのモデルの雰囲気を混ぜた「なんちゃって数式」表記です。
テキストの数式とほぼ同じです（テキストの詳細記載に感謝です！）。

$$
\begin{align*}
\mu_j &\sim \text{Uniform}(0, 100) \\
\sigma_e &\sim \text{Uniform}(0, 100) \\
likelihood &\sim \text{Normal}(\text{mu}=\mu_j,\ \text{sigma}=\sigma_e) \\
\end{align*}
$$

１．血液型インデックスの作成
blood_idxはカテゴリ変数「血液型」の要素$${\{A,\ B,\ O,\ AB\}}$$を次の整数値に置き換えたものです。

0：Ａ型、1：Ｂ型、2：Ｏ型、3：ＡＢ型

PyMCのConstantDataに定義して利用します。

### 血液型のインデックスの作成
# 血液型を0:A, 1:B, 2:O, 3:ABの順番に変換して、blood_idxに格納
# PyMCのConstantDataで利用

# 血液型をidxに仮格納
blood_idx = data['血液型'].values

# A:0、B:1、O:2、AB:3に変換
blood_idx = np.where(blood_idx=='A', 0,
            np.where(blood_idx=='B', 1,
            np.where(blood_idx=='O', 2,
            np.where(blood_idx=='AB', 3, 9))))
blood_idx = blood_idx.astype(int)

# idxの表示
blood_idx

【実行結果】

２．モデルの定義
coord、data、パラメータの事前分布、尤度、後から利用する計算値をそれぞれ指定します。

### モデルの定義

with pm.Model() as model:

    ## データ関連定義
    # coordの定義
    model.add_coord('data', values=data.index, mutable=True)
    model.add_coord('blood', values=['A', 'B', 'O', 'AB'], mutable=True)
    # dataの定義
    y = pm.ConstantData('y', value=data['持続'], dims='data')
    bloodIdx = pm.ConstantData('bloodIdx', value=blood_idx, dims='data')

    ## パラメータの事前分布
    mu = pm.Uniform('mu', lower=0, upper=100, dims='blood')
    sigmaE = pm.Uniform('sigmaE', lower=0, upper=100)
    
    ## 尤度
    likelihood = pm.Normal('likelihood', mu=mu[bloodIdx], sigma=sigmaE,
                           observed=y, dims='data')
    
    ## 計算値
    # 全平均 muAll
    muAll = pm.Deterministic('muAll', pt.mean(mu))
    # 要因の効果の標準偏差 sigmaA
    sigmaA = pm.Deterministic('sigmaA', pt.std(mu))
    # 分散説明率 eta2
    eta2 = pm.Deterministic('eta2',
                            pt.sqr(sigmaA) / (pt.sqr(sigmaA) + pt.sqr(sigmaE)))

【モデル注釈】

coordの定義
座標に名前を付けたり、その座標が取りうる値を設定できます。
今回は次の２つを設定しました。
・行の座標：名前「data」、値「行インデックス」
・血液型の座標：名前「blood」、値「A、B、O、AB」
dataの定義
目的変数$${y}$$と血液型インデックス$${bloodIdx}$$を設定しました。
パラメータの事前分布
muの次元は血液型であり、coordで指定した「blood」を指定します。
尤度
muはdataで定義した血液型インデックスを利用して「mu[bloodIdx]」とします。
計算値
テキストの表2.4で用いる全平均$${\mu}$$：muAll、要因の効果の標準偏差$${\sigma_a}$$：sigmaA、分散説明率$${\eta^2}$$：eta2を計算します。
- 分散説明率$${\eta^2=\cfrac{\sigma_a^2}{\sigma_a^2 + \sigma_e^2}}$$です。
- pytensor.tensorの関数を利用します。pm.mathよりもコードを短く書けます。
  - pt.mean()は平均の計算。pt.mean($${\mu}$$)は$${\mu}$$の全平均です。
  - pt.std()は標準偏差の計算。pt.std($${\mu}$$)は$${\mu}$$の標準偏差です。
  - pt.sqr()はニ乗の計算。pt.sqr($${\sigma_a}$$)=$${\sigma_a^2}$$です。

３．モデルの外観の確認

### モデルの表示
model

【実行結果】

### モデルの可視化
pm.model_to_graphviz(model)

【実行結果】

MCMCの実行

１．事後分布からのサンプリング
乱数生成数（draws, tune, chains）はテキストどおりです。
nuts_sampler='numpyro'とすることで、numpyroをNUTSサンプラーに利用できます。
処理時間は２０秒でした。

### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用 20秒
with model:
    idata = pm.sample(draws=20000, tune=1000, chains=5, target_accept=0.95, 
                      nuts_sampler='numpyro', random_seed=1234)

【実行結果】省略

２．サンプリングデータの確認
$${\hat{R}}$$、事後分布の要約統計量、トレースプロットを確認します。
事後分布の収束確認はテキストにならって$${\hat{R} \leq 1.1}$$としています。

### r_hat>1.1の確認
rhat_idata = az.rhat(idata)
(rhat_idata>1.1).sum()

【実行結果】
$${\hat{R} > 1.1}$$のパラメータは「0」件です。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。

事後分布の要約統計量です。
テキストの表2.4、表2.5の代替です。

### 推論データの要約統計情報の表示 ★表2.4、2.5に対応
var_names = ['muAll', 'sigmaA', 'eta2', 'mu', 'sigmaE']
pm.summary(idata, var_names=var_names, hdi_prob=0.95)

【実行結果】
統計量は上から、$${\mu}$$、$${\sigma_a}$$、$${\eta^2}$$、$${\mu_A}$$、$${\mu_B}$$、$${\mu_O}$$、$${\mu_{AB}}$$、$${\sigma_e}$$です。
EAP（mean）、post.sd（sd）、2.5%（hdi_2.5%）、97.5%（hdi_97.5%）の値はテキストとほぼ同じです！（やったー！）
なお、テキストはの95%区間は信用区間ですが、summary関数の95%区間はHDI区間です。

【分析】
分散説明率$${\eta^2}$$は、血液型が性格「持続」の得点をどの程度説明しているかを表す指標です。
$${\eta^2}$$のEAP＝点推定値は$${0.7\%}$$とかなり小さな値です。
血液型が持続得点の$${\boldsymbol{0.7\%}}$$しか説明していないということは、血液型で性格「持続」が分かるとは言い難い、ということのようです。

トレースプロットです。

### トレースプロットの描画
pm.plot_trace(idata, var_names=var_names, compact=False)
plt.tight_layout();

【実行結果】
きれいなトレースプロットです。収束している感触を満喫しました。

分析

１．平均値差に関連する推定量の計算
テキストの表2.6、表2.7の推定量を計算してpandasのデータフレームに格納します。

### 「持続」の平均値差について、A型とO型、A型とAB型の比較数値を計算
# 事後分布からサンプリングした 100000個のデータを用いて推定する

## numpy配列のEAP, std, 2.5%/97.5%quantileを返す関数の定義
def calc_estimator(dat):
    return (np.mean(dat), np.std(dat), np.quantile(dat, 0.025), 
            np.quantile(dat, 0.975))

## 推論データの変数の取り出し
# 尤度の血液型別平均データ shape=(100000, 4)
# A型:mu[:, 0], B型:mu[:, 1], O型:mu[:, 2], AB型:mu[:, 3]
mu = idata.posterior.mu.data.reshape(100000, 4)
# 尤度の標準偏差データ shape=(100000, )
sigma_E = idata.posterior.sigmaE.data.flatten()

## A型とO型の平均値差に関する推定値の計算
# 平均値差μA-μO, 効果量δ, 非重複度U3, 優越率πd
mu_diff_A_O = mu[:, 0] - mu[:, 2]
delta_A_O = mu_diff_A_O / sigma_E
U3_A_O = stats.norm.cdf(mu[:, 0], mu[:, 2], sigma_E)
pi_A_O = stats.norm.cdf(delta_A_O / np.sqrt(2), 0, 1)
# 推定値のデータフレーム化
df_A_O = pd.DataFrame({'μA-μO': calc_estimator(mu_diff_A_O),
                       '効果量_δ': calc_estimator(delta_A_O),
                       '非重複度_U3': calc_estimator(U3_A_O),
                       '優越率_πd': calc_estimator(pi_A_O)},
                       index=['EAP', 'post.sd', '2.5%', '97.5%']).T


## A型とAB型の平均値差に関する推定値の計算
# 平均値差μA-μAB, 効果量δ, 非重複度U3, 優越率πd
mu_diff_A_AB = mu[:, 0] - mu[:, 3]
delta_A_AB = mu_diff_A_AB / sigma_E
U3_A_AB = stats.norm.cdf(mu[:, 0], mu[:, 3], sigma_E)
pi_A_AB = stats.norm.cdf(delta_A_AB / np.sqrt(2), 0, 1)
# 推定値のデータフレーム化
df_A_AB = pd.DataFrame({'μA-μAB': calc_estimator(mu_diff_A_AB),
                        '効果量_δ': calc_estimator(delta_A_AB),
                        '非重複度_U3': calc_estimator(U3_A_AB),
                        '優越率_πd': calc_estimator(pi_A_AB)},
                        index=['EAP', 'post.sd', '2.5%', '97.5%']).T

【実行結果】なし

【計算式】
統計量に関するテキストの説明とRコードの計算式を引用させていただき、Ａ型とＯ型の差を例にして書きます。

■ 効果量：$${\delta=\cfrac{\mu_A - \mu_O}{\sigma_e}}$$
効果量$${\delta}$$の値を10倍すると偏差値のように平均値差を解釈できるそうです。

■ 非重複度：$${U_3=F(x=\mu_A \mid \text{mu}=\mu_O,\ \text{sigma}=\sigma_e)}$$
$${F}$$は正規分布の累積分布関数です。Norm.CDFです。
Ａ型の平均値$${\mu_A}$$がＯ型の分布の何％点に位置するかを表すそうです。
50％点に位置する場合、Ａ型とＯ型は完全に重複していると解釈されます。

■ 優越率：$${\pi_d=F \left(x=\delta / \sqrt{2} \mid \text{mu}=0,\ \text{sigma}=1 \right)}$$
標準正規分布の累積分布関数です。
Ａ型からランダムに選ばれた測定値が、Ｏ型からランダムに選ばれた測定値より大きい確率を表すそうです。

テキストより一部改変して引用

では、計算した推定値を表示します。

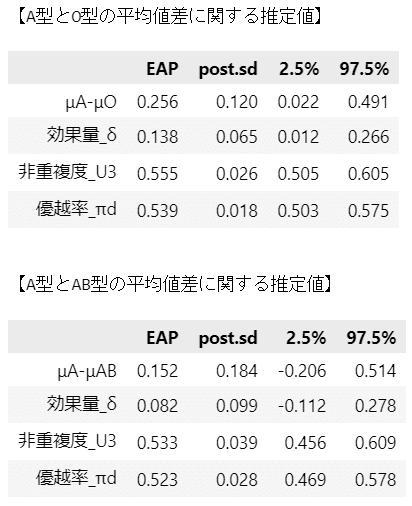
### 平均値差に関する推定値の表示 ★表2.6、2.7に対応 ★AとABの値がテキストと異なる

print('【A型とO型の平均値差に関する推定値】')
display(df_A_O.round(3))

print('\n【A型とAB型の平均値差に関する推定値】')
display(df_A_AB.round(3))

【実行結果】
Ａ型とＯ型の推定値はテキストとほぼ同じ値です！（やったー！）
しかし、Ａ型とＡＢ型の推定値はテキストと大きく異なります（がーん）。

【推定値の評価】
事後分布の要約統計量の値を用いると$${\mu_A}$$の平均$${4.588-\mu_{AB}}$$の平均$${4.436=0.152}$$となり、この表の$${\mu_A - \mu_{AB}}$$のEAP$${0.152}$$と一致するのです。
なので、この推定値が適切であると仮定して、分析を進めます！

【分析】
テキストの分析の仕方を利用させていただき、書きます。
概して、血液型による性格「持続」の差があるとしても些細な差であり、実質的に意味のある差とは考えにくい、ということのようです。

■ Ａ型とＯ型の平均値差
効果量$${\delta}$$（偏差値換算）はＡ型のほうがＯ型よりも$${1.38}$$ほど「持続」の得点が高い。
　→偏差値的に差はほとんど無いと言えるかも？
非重複度$${U_3}$$はＡ型の「持続」の得点の平均値はＯ型の$${55.5\%}$$あたりに位置する。Ａ型の方が$${5.5\%}$$分だけ「持続」の高い人が多いことを示す。
　→$${5.5\%}$$という違いは小さいと言えるかも？
優越率$${\pi_d}$$はランダムにＡ型の人とＯ型の人を選んで比較すると$${53.9\%}$$の確率でＡ型の人の「持続」の得点が高いことを示す。
　→$${53.9\%}$$程度の確率の高さは差が小さいと言えるのかも？

■ Ａ型とＡＢ型の平均値差
効果量$${\delta}$$（偏差値換算）はＡ型のほうがＡＢ型よりも$${0.82}$$ほど「持続」の得点が高い。
　→偏差値的に差はほとんど無いと言えるかも？
非重複度$${U_3}$$はＡ型の「持続」の得点の平均値はＡＢ型の$${53.3\%}$$あたりに位置する。Ａ型の方が$${3.3\%}$$分だけ「持続」の高い人が多いことを示す。
　→$${3.3\%}$$という違いは小さいと言えるかも？
優越率$${\pi_d}$$はランダムにＡ型の人とＡＢ型の人を選んで比較すると$${52.3\%}$$の確率でＡ型の人の「持続」の得点が高いことを示す。
　→$${52.3\%}$$程度の確率の高さは差が小さいと言えるのかも？

最後にこれらの推定値をヒストグラムに描画しましょう。

### A型とO型の平均値差に関する推定値のヒストグラムの描画

plt.figure(figsize=(8, 4))
# ヒストグラムの描画（平均値差）
plt.hist(mu_diff_A_O, bins=50, density=True, histtype='step', 
         label=r'平均値差 $\mu_A-\mu_O$')
# ヒストグラムの描画（効果量）
plt.hist(delta_A_O, bins=50, density=True, histtype='step', 
         label=r'効果量 $\delta$')
# ヒストグラムの描画（非重複度）
plt.hist(U3_A_O, bins=50, density=True, histtype='step',
         label=r'非重複度 $U_3$')
# ヒストグラムの描画（優越率）
plt.hist(pi_A_O, bins=50, density=True, histtype='step',
         label=r'優越率 $\pi_d$')
# 修飾
plt.xticks(np.arange(-0.3, 0.9, 0.1))
plt.title('A型とO型の平均値差に関する推定値のヒストグラム')
plt.xlabel('推定値')
plt.ylabel('確率密度')
plt.legend(loc='upper left')
plt.show()

【実行結果】

### A型とAB型の平均値差に関する推定値のヒストグラムの描画

plt.figure(figsize=(8, 4))
# ヒストグラムの描画（平均値差）
plt.hist(mu_diff_A_AB, bins=50, density=True, histtype='step', 
         label=r'平均値差 $\mu_A-\mu_{AB}$')
# ヒストグラムの描画（効果量）
plt.hist(delta_A_AB, bins=50, density=True, histtype='step', 
         label=r'効果量 $\delta$')
# ヒストグラムの描画（非重複度）
plt.hist(U3_A_AB, bins=50, density=True, histtype='step',
         label=r'非重複度 $U^3$')
# ヒストグラムの描画（優越率）
plt.hist(pi_A_AB, bins=50, density=True, histtype='step',
         label=r'優越率 $\pi_d$')
# 修飾
plt.xticks(np.arange(-0.6, 1.1, 0.1))
plt.title('A型とAB型の平均値差に関する推定値のヒストグラム')
plt.xlabel('推定値')
plt.ylabel('確率密度')
plt.legend(loc='upper left')
plt.show()

【実行結果】

２．推論データ（idata）の保存
推論データを再利用する場合に備えてファイルに保存しましょう。
idataをpickleで保存します。

### idataの保存 pickle
file = r'idata_ch02.pkl'
with open(file, 'wb') as f:
    pickle.dump(idata, f)

読み込みコードは次のとおりです。

### idataの読み込み pickle
file = r'idata_ch02.pkl'
with open(file, 'rb') as f:
    idata_load = pickle.load(f)

３．おまけ
Ａ型とＢ型の平均値差の推定値も計算しましょう。

### A型とB型の平均値差に関する推定値の計算
# 平均値差μA-μB, 効果量δ, 非重複度U3, 優越率πd
mu_diff_A_B = mu[:, 0] - mu[:, 1]
delta_A_B = mu_diff_A_B / sigma_E
U3_A_B = stats.norm.cdf(mu[:, 0], mu[:, 1], sigma_E)
pi_A_B = stats.norm.cdf(delta_A_B / np.sqrt(2), 0, 1)
# 推定値のデータフレーム化
df_A_B = pd.DataFrame({'μA-μB': calc_estimator(mu_diff_A_B),
                       '効果量_δ': calc_estimator(delta_A_B),
                       '非重複度_U3': calc_estimator(U3_A_B),
                       '優越率_πd': calc_estimator(pi_A_B)},
                       index=['EAP', 'post.sd', '2.5%', '97.5%']).T

print('\n【A型とB型の平均値差に関する推定値】')
display(df_A_B.round(3))

【実行結果】
実は、Ａ型とＢ型の差がもっとも大きく、効果量・非重複度・優越率の全てが他の血液型よりも高い値になっています。
高いと入っても、おそらく、Ｏ型・ＡＢ型の分析と同様に、実質的に意味のある差では無かろう、という結論になりそうです。
なお、テキストはＢ型を取り上げていませんが、ＲスクリプトはＢ型を取り上げています（ＲスクリプトではＡ型とＯ型、Ａ型とＢ型を比較）。

恒例のヒストグラムを描画してみます。

### A型とB型の平均値差に関する推定値のヒストグラムの描画

plt.figure(figsize=(8, 4))
# ヒストグラムの描画（平均値差）
plt.hist(mu_diff_A_B, bins=50, density=True, histtype='step', 
         label=r'平均値差 $\mu_A-\mu_B$')
# ヒストグラムの描画（効果量）
plt.hist(delta_A_B, bins=50, density=True, histtype='step', 
         label=r'効果量 $\delta$')
# ヒストグラムの描画（非重複度）
plt.hist(U3_A_B, bins=50, density=True, histtype='step',
         label=r'非重複度 $U^3$')
# ヒストグラムの描画（優越率）
plt.hist(pi_A_B, bins=50, density=True, histtype='step',
         label=r'優越率 $\pi_d$')
# 修飾
plt.xticks(np.arange(-0.3, 1.0, 0.1))
plt.title('A型とB型の平均値差に関する推定値のヒストグラム')
plt.xlabel('推定値')
plt.ylabel('確率密度')
plt.legend(loc='upper left')
plt.show()

【実行結果】

以上で第２章は終了です。

おわりに

血液型と性格の関係、優しいモデル

「血液型による性格診断の信ぴょう性」
長きにわたる論争は決着できるのでしょうか？
個人的には、人々が血液型性格診断に触れることによって、あたかも洗脳の如く、性格診断内容に合った振る舞いをするようになる、こんな気がします。
なので、血液型性格診断が流行している間は、血液型と性格に関係があるように感じ続けるのだと思います。

ところで、今回は初学者にとって優しいモデルでした。
尤度に正規分布、パラメータ$${\mu,\ \sigma}$$の事前分布に一様分布を用いたシンプルな構成です。
$${\mu}$$は「血液型」の要素ごとに設定しました。
ベイズモデリングの基本を学べる「やさしい」テーマです。
また、血液型間の差について、「差の検定」などの伝統的な統計的仮説検定との比較で、事後分布からのサンプルデータに基づくベイズ流の分析は斬新に感じます。
シンプルで力強いこの分析をしっかり身につけたいと思います。

シリーズの記事

次の記事

前の記事

ブログの紹介

note で４つのシリーズ記事を書いています。
ぜひ覗いていってくださいね！

１．のんびり統計
統計検定２級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定２級公式問題集CBT対応版に対応しています。

２．RとStanではじめる心理学のための時系列分析入門を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析トピックを PythonとPyMC Ver.5で取り組みます。
豊富なテーマ（お題）を実践することによって、PythonとPyMCの基礎体力づくりにつながる、そう信じています。
日々、Web検索に勤しみ、時系列モデルの理解、Pythonパッケージの把握、R・Stanコードの翻訳に励んでいます！
このシリーズがPython時系列分析の入門者の参考になれば幸いです🍀

３．Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learn と PyTorch の教科書です。
よかったらぜひ、お試しくださいませ。

４．データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Python のコラムを不定期に綴っています。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
ベイズ書籍の実践記録も掲載中です。

最後までお読みいただきまして、ありがとうございました。

第２章「血液型と性格には関連がある？」のベイズモデリングをPyMC Ver.5 で

サマリー

テキストの概要

自己評価

モデルの概要

テキストの調査・実験の概要

テキストのモデリング

PyMC実装

準備・データ確認

モデル構築

MCMCの実行

分析

おわりに

血液型と性格の関係、優しいモデル

シリーズの記事

ブログの紹介

いいなと思ったら応援しよう！