
「数値シミュレーションで読み解く統計のしくみ」をPythonで写経 ~ 第4章4.2「母平均の信頼区間」
第4章「母数の推定のシミュレーション」
書籍の著者 小杉考司 先生、紀ノ定保礼 先生、清水裕士 先生
この記事は、テキスト「数値シミュレーションで読み解く統計のしくみ」第4章「母数の推定のシミュレーション」4.2節「母平均の信頼区間」の Python写経活動 を取り扱います。
今回はシミュレーションを通じて母平均の信頼区間とお友達になります。
信頼区間の%は母平均の確率じゃないアレの図も出現です!
R の基本的なプログラム記法はざっくり Python の記法と近いです。
コードの文字の細部をなぞって、R と Python の両方に接近してみましょう!
ではテキストを開いてシミュレーションの旅に出発です🚀

はじめに
テキスト「数値シミュレーションで読み解く統計のしくみ」のご紹介
このシリーズは書籍「数値シミュレーションで読み解く統計のしくみ〜Rでためしてわかる心理統計」(技術評論社、「テキスト」と呼びます)の Python写経です。
テキストは、2023年9月に発売され、副題「Rでためしてわかる心理統計」のとおり、統計処理に定評のある R の具体的なコードを用いて、心理統計の理解に役立つ数値シミュレーションを実践する素晴らしい書籍です。
引用表記
この記事は、出典に記載の書籍に掲載された文章及びコードを引用し、適宜、掲載文章とコードを改変して書いています。
【出典】
「数値シミュレーションで読み解く統計のしくみ〜Rでためしてわかる心理統計」初版第1刷、著者 小杉考司・紀ノ定保礼・清水裕士、技術評論社
記事中のイラストは、「かわいいフリー素材集いらすとや」さんのイラストをお借りしています。
ありがとうございます!
4.2 母平均の信頼区間
標本平均などは点推定と呼ばれ、特定の1点を指しています。
一方で、母数の推定を一定区間で表すのが区間推定です。
この記事は Jupyter Notebook 形式(拡張子 .ipynb)でPythonコードを書きます。
概ね確率分布の特性値算出には scipy.stats を用い、乱数生成には numpy.random.generator を用いるようにしています。
主に利用するライブラリをインポートします。
### インポート
# 数値計算
import numpy as np
# 確率・統計
import scipy.stats as stats
# 描画
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'Meiryo'
■ 点推定が常に間違えることをシミュレーション
母集団から抽出する標本は母集団のサイズよりも(かなり?)小さいので、テキストは「点推定は常に間違える」としています。
標本平均を例にして、標本平均が母平均と常に一致しないことをシミュレーションします。
母集団分布に平均0、標本平均1の正規分布を仮定して正規分布乱数を10個生成し標本平均を取る、この処理を10000回繰り返します。
標本平均が母平均の0と一致する割合を計算します。
### 145ページ サンプルサイズが小さい限り点推定は常に間違えるの検証
## 設定と準備
mu = 0 # 母平均
sigma = 1 # 母標準偏差
n = 10 # サンプルサイズ
iter = 10000 # 標本を得る回数(標本数)
## シミュレーション
rng = np.random.default_rng(seed=0)
# for文に代えてリスト内包表記を利用
sample_mean = np.array(
[rng.normal(size=n, loc=mu, scale=sigma).mean() for _ in range(iter)])
## 結果 標本平均=母平均μの比率を計算
(sample_mean == mu).sum() / iter【実行結果】
標本平均が母平均と一致した割合は0!
「点推定は常に間違える」のです!


4.2.1 母分散 σ² が既知の場合
テキストは147~148ページにかけて次の式で表される、標本平均$${\bar{X}}$$を用いた母平均$${\mu}$$の95%信頼区間を解説しています。
$$
\bar{X} - 1.96 \cfrac{\sigma}{\sqrt{n}} \leq \mu \leq \bar{X} + 1.96 \cfrac{\sigma}{\sqrt{n}}
$$
説明に用いられる図4.15、図4.16の描画をコード化してみます。
### 147ページの図4.15
## 設定
mu = 0 # 母平均
xbar1 = 0.2 # 標本平均の実現値1
xbar2 = 1.3 # ずらした正規分布の平均
var = 1 # 母分散
se = np.sqrt(var / n) # 標準誤差
n = 10 # 標本サイズ
## 描画
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10, 3))
## 左のプロット
# 平均0、分散1の正規分布の確率密度関数の描画
line_x = np.linspace(-3, 3, 1001)
ax1.plot(line_x, stats.norm.pdf(line_x, loc=mu, scale=np.sqrt(var/n)),
color='tab:orange')
# 平均0.2、分散1の正規分布の確率密度関数の描画
ax1.plot(line_x, stats.norm.pdf(line_x, loc=xbar1, scale=np.sqrt(var/n)),
color='tab:blue')
# 平均0.2、分散1の正規分布の95%信頼区間の塗りつぶし
line_x_95 = np.linspace(xbar1 - 1.96*se, xbar1 + 1.96*se, 1001)
ax1.fill_between(line_x_95, 0, stats.norm.pdf(line_x_95, loc=xbar1, scale=se),
color='tab:blue', alpha=0.2)
# 平均0.2、分散1の正規分布の95%信頼区間の端線の描画
ax1.hlines(0, line_x_95.min(), line_x_95.max(), color='tab:blue', lw=0.5)
ax1.vlines(line_x_95.min(),
0, stats.norm.pdf(line_x_95.min(), loc=xbar1, scale=se),
color='tab:blue', lw=0.5)
ax1.axvline(line_x_95.max(), color='tab:blue', lw=0.5)
# 平均0.2、分散1の正規分布の平均の垂直線の描画
ax1.axvline(xbar1, color='tab:red', ls='--', lw=0.8)
## 右のプロット
# 平均0、分散1の正規分布の確率密度関数の描画
line_x = np.linspace(-3, 3, 1001)
ax2.plot(line_x, stats.norm.pdf(line_x, loc=mu, scale=np.sqrt(var/n)),
color='tab:orange')
# 平均1.3、分散1の正規分布の確率密度関数の描画
ax2.plot(line_x, stats.norm.pdf(line_x, loc=xbar2, scale=np.sqrt(var/n)),
color='tab:blue')
# 平均1.3、分散1の正規分布の95%信頼区間の塗りつぶし
line_x_95 = np.linspace(xbar2 - 1.96*se, xbar2 + 1.96*se, 1001)
ax2.fill_between(line_x_95, 0, stats.norm.pdf(line_x_95, loc=xbar2, scale=se),
color='tab:blue', alpha=0.2)
# 平均1.3、分散1の正規分布の95%信頼区間の端線の描画
ax2.hlines(0, line_x_95.min(), line_x_95.max(), color='tab:blue', lw=0.5)
ax2.axvline(line_x_95.min(), color='tab:blue', lw=0.5)
ax2.vlines(line_x_95.max(),
0, stats.norm.pdf(line_x_95.max(), loc=xbar2, scale=se),
color='tab:blue', lw=0.5)
# 平均1.3、分散1の正規分布の平均の垂直線の描画
ax2.axvline(xbar2, color='tab:red', ls='--', lw=0.8)
plt.tight_layout();【実行結果】

### 148ページの図4.16
## 設定
mu = 0 # 母平均
xbar = 0.75 # 標本平均の実現値
var = 1 # 母分散
n = 10 # 標本サイズ
std = np.sqrt(var / n) # 標準誤差
## 描画
# 描画領域の設定
plt.figure(figsize=(6, 3))
# 平均0、分散1の正規分布の確率密度関数の描画
line_x1 = np.linspace(-3, 3, 1001)
plt.plot(line_x1, stats.norm.pdf(line_x1, loc=mu, scale=np.sqrt(var/n)),
color='tab:blue')
# 標本平均の実現値0.75の垂直線の描画
plt.axvline(xbar, color='tab:red', lw=0.8, label=rf'$\bar{{x}}$={xbar}')
# 95%信頼区間の実現地の下限5の垂直点線の描画
plt.axvline(xbar-1.96*std, color='tab:red', ls='--', lw=0.8,
label='$\mu$の95%信頼区間')
# 95%信頼区間の実現地の上限5の垂直点線の描画
plt.axvline(xbar+1.96*std, color='tab:red', ls='--', lw=0.8)
# タイトル・y軸ラベルの設定
plt.title(f'$\mu$={mu}, $\sigma^2$={var}, n={n}の標本分布と95%信頼区間')
plt.ylabel('density')
# 凡例表示の設定
plt.legend();【実行結果】


■ 95% 信頼区間は本当に95%の確率で真となるかシミュレーション
・母分散$${\sigma^2=1}$$
・母平均分布は正規分布
・サンプルサイズ$${n=10}$$
のとき、母平均の95%信頼区間$${\bar{X} - 1.96 \cfrac{\sigma}{\sqrt{10}} \leq \mu \leq \bar{X} + 1.96 \cfrac{\sigma}{\sqrt{10}}}$$が95%の確率で真になるか、正規分布乱数の平均値を10000個生成してシミュレーションします。
### 149ページ 標本平均の実現値→信頼区間の実現値が母平均を含むかのシミュレーション
## 設定と準備
n = 10 # サンプルサイズ
mu = 0 # 母平均
sigma = 1 # 母標準偏差
se = sigma / np.sqrt(n) # 標準誤差
iter = 10000 # 標本を得る回数(標本数)
## シミュレーション
rng = np.random.default_rng(seed=123)
sample_mean = np.array(
[rng.normal(size=n, loc=mu, scale=sigma).mean() for _ in range(iter)])
## 結果 95%信頼区間に母平均を含む比率を計算
true_num = ((sample_mean - 1.96*se <= mu) & (mu <= sample_mean + 1.96*se)).sum()
true_num / iter【実行結果】
約 95% で真になりました!これぞ、95%信頼区間!
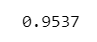
■ 標本平均から95%信頼区間の実現値を算出して母平均を含むかシミュレーション
上記で生成した10000個の標本平均から30個をランダムに抽出して、各標本平均の値から95%信頼区間の実現値を計算し、95%信頼区間の実現値に母平均0を含むかどうかを可視化します。
### 150ページ 図4.17
## sample_meanからランダムに30個を非復元抽出
rng = np.random.default_rng(seed=7)
x_bar_samples = rng.choice(a=sample_mean, size=30, replace=False)
## 描画
# 描画領域の設定
plt.figure(figsize=(10, 4))
# 線色の設定(母平均を含む:青色、含まない:赤色)
colors = ['tab:blue', 'tab:red']
# 30個のサンプルごとに95%信頼区間の実現値算出とエラーバー描画を繰り返し処理
for i, x_bar in enumerate(x_bar_samples):
# 95%信頼区間の下端・上端を算出
lower = x_bar - 1.96 * se
upper = x_bar + 1.96 * se
# errbarの長さ(上・下同じ)を算出
yerr = 1.96 * se
# 95%信頼区間の実現値に母平均を含まないとき、outer区分に1を設定
outer = ((lower > mu) | (upper < mu)) * 1
# エラーバーの描画
plt.errorbar(x=i, y=x_bar, yerr=yerr, capsize=4, marker='o',
color=colors[outer])
# 母平均0の水平線の描画
plt.axhline(mu, color='tab:red', ls='--')
# x軸ラベル、y軸ラベルの設定
plt.xlabel('index')
plt.ylabel('sample mean');【実行結果】
27個が母平均0を含んでいます。
そして30個の95%は28.5個です。
標本平均の数のうち95%が母平均を含んでいると言えそうです。
(母平均がこの区間に含まれる確率は95%、と言ってはいけないアレです)

■ 95%信頼区間シミュレーションを10000000個の乱数で実施
テキストいわく「サンプルサイズが母集団サイズに満たない限り、95%信頼区間の実現値が母数を含んでいるという判断は、必ず5%の確率で間違えます」。
テキストのとおり、サンプルサイズを1千万個にして確かめます。
以下の処理は約25分かかりました。
### 150ページ 図4.18 25分
## 設定と準備
n = 10000000 # サンプルサイズ
mu = 0 # 母平均
sigma = 1 # 母標準偏差
se = sigma / np.sqrt(n) # 標準誤差
iter = 10000 # 標本を得る回数(標本数)
## シミュレーション
rng = np.random.default_rng(seed=123)
sample_mean = np.array(
[rng.normal(size=n, loc=mu, scale=sigma).mean() for _ in range(iter)])## sample_meanからランダムに30個を非復元抽出
rng = np.random.default_rng(seed=0)
x_bar_samples = rng.choice(a=sample_mean, size=30, replace=False)
## 描画
# 描画領域の設定
plt.figure(figsize=(10, 4))
# 線色の設定(母平均を含む:青色、含まない:赤色)
colors = ['tab:blue', 'tab:red']
# 30個のサンプルごとに95%信頼区間の実現値算出とエラーバー描画を繰り返し処理
for i, x_bar in enumerate(x_bar_samples):
# 95%信頼区間の下端・上端を算出
lower = x_bar - 1.96 * se
upper = x_bar + 1.96 * se
# errbarの長さ(上・下同じ)を算出
yerr = 1.96 * se
# 95%信頼区間の実現値に母平均を含まないとき、outer区分に1を設定
outer = ((lower > mu) | (upper < mu)) * 1
# エラーバーの描画
plt.errorbar(x=i, y=x_bar, yerr=yerr, capsize=4, marker='o',
color=colors[outer])
# 母平均0の水平線の描画
plt.axhline(mu, color='tab:red', ls='--')
# x軸ラベル、y軸ラベルの設定
plt.xlabel('index')
plt.ylabel('sample mean');【実行結果】
縦軸の標本平均の値は前のグラフと比べてかなり小さくなっていますが、母平均を含む数 27 は同じになりました。


4.2.2 母分散 σ² が未知の場合
母分散が既知の場合と未知の場合(通常の場合)の標本平均の標本分布を比べます。
■ 母分散が既知の場合の標本平均の標本分布
$$
\cfrac{\bar{X} - \mu}{\sigma / \sqrt{n}} \sim \text{Normal}\ (0, 1)
$$
■ 母分散が未知の場合の標本平均の標本分布
母分散$${\sigma^2}$$を不偏分散$${U^2}$$で置き換えた統計量$${T}$$(次の数式の左辺)は自由度$${n-1}$$のt分布に従います。
$$
\cfrac{\bar{X} - \mu}{U / \sqrt{n}} \sim \text{t}\ (n-1) \\
$$
母分散が未知の場合、統計量$${T}$$の標本分布が自由度$${n-1}$$のt分布であることを利用して、母平均の区間推定を行います。

■ 母分散既知・未知がそれぞれ従う確率分布をシミュレーションで比べる
平均 30、標準偏差 3 の正規分布乱数 10個から標本平均を算出する処理を10000 回繰り返し、母分散既知と未知の分布を描きます。
### 151ページ 母分散が既知と未知のケースを比較 152ページ図4.19
## 設定と準備
mu = 30 # 母平均
sigma = 3 # 母標準偏差
n = 10 # サンプルサイズ
iter = 10000 # 標本を得る回数(標本数)
## シミュレーション
# 乱数生成
rng = np.random.default_rng(seed=123)
rnd = np.array([rng.normal(size=n, loc=mu, scale=sigma) for _ in range(iter)])
# 統計量の算出
z = (rnd.mean(axis=1) - mu) / (sigma / np.sqrt(n)) # 母分散が既知
t = (rnd.mean(axis=1) - mu) / (rnd.std(ddof=1, axis=1) / np.sqrt(n)) # 母分散が未知
## 結果
line_x = np.linspace(-4, 4, 1001)
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10, 3.5), sharex=True)
# 母分散が既知のとき
ax1.hist(z, bins=30, density=True, ec='white', alpha=0.7)
ax1.plot(line_x, stats.norm.pdf(line_x, loc=0, scale=1), linewidth=2,
color='tab:red')
ax1.set(xlabel='z', ylabel='Density', title='Histogram of z')
# 母分散が未知のとき
ax2.hist(t, bins=30, density=True, ec='white', alpha=0.7)
ax2.plot(line_x, stats.t.pdf(line_x, df=n - 1), linewidth=2, color='tab:red')
ax2.set(xlabel='t', ylabel='Density', title='Histogram of t')
plt.tight_layout();【実行結果】
左が母分散既知(赤い線は標準正規分布)、左が母分散未知(赤い線は自由度 9 のt分布)です。
よく似てますが中身は異なります。

■ 標本平均 ± 1.96 標準偏差の区間が95%信頼区間か?
t分布の場合、平均 ± 1.96 標準偏差の区間が95%にならないことを正規分布と対比して確認します。
マジックナンバー 1.96 がt分布にも通用するのかのシミュレーションです。
自由度 20 のt分布を想定します。
このt分布の標準偏差は$${20/(20-2)=20/18=10/9}$$です。
### 153ページ 正規分布とt分布の平均±1.96標準偏差の区間が占める割合
# 設定と準備
nu = 20 # t分布の自由度パラメータ
sigma = np.sqrt(nu / (nu - 2)) # t分布の標準偏差
# 正規分布の場合
stats.norm.cdf(x=1.96*sigma, loc=0, scale=sigma) \
- stats.norm.cdf(x=-1.96*sigma, loc=0, scale=sigma)【実行結果】
正規分布の場合は95%に近似します。

### 154ページ 続き
# t分布の場合
stats.t.cdf(x=1.96*sigma, df=nu) \
- stats.t.cdf(x=-1.96*sigma, df=nu)【実行結果】
t分布の場合、95%から少しずれています。


■ 母分散未知の母平均の95%信頼区間の計算
母集団分布が母平均 50、母標準偏差 10(未知のテイで!)の正規分布のケースで母平均の95%信頼区間を計算します。
サンプルサイズは 15 です。
段階的に進みます。
上記の母集団分布に従う乱数を15個生成して、標本平均を算出します。
### 154ページ t分布を用いて母平均μの信頼区間の実現値を算出
n = 15 # サンプルサイズ
mu = 50 # 母平均
sigma = 10 # 母標準偏差
rng = np.random.default_rng(seed=5)
rnd = rng.normal(size=n, loc=mu, scale=sigma)
rnd.mean() # 標本平均【実行結果】
標本平均はおよそ 50.15 です。

標本の不偏分散の正の平方根です。
### 155ページ 続き
rnd.std(ddof=1) # 不偏分散の正の平方根【実行結果】
標本の不偏分散の正の平方根はおよそ 9.71 です。

95%信頼区間の下限を計算します。
自由度 14 のt分布の 97.5パーセンタイル値は scipy.stats の t.ppf() で算出します。
### 155ページ 続き
# 信頼区間の下限の実現値
rnd.mean() - stats.t.ppf(q=0.975, df=n-1) * (rnd.std(ddof=1) / np.sqrt(n))【実行結果】
95%信頼区間の下限の実現値はおよそ 44.77 です。

95%信頼区間の上限を計算します。
### 155ページ 続き
# 信頼区間の上限の実現値
rnd.mean() + stats.t.ppf(q=0.975, df=n-1) * (rnd.std(ddof=1) / np.sqrt(n))【実行結果】
95%信頼区間の上限の実現値はおよそ 55.53 です。

答え合わせをします。
テキストは R の t.test() 関数を利用して答え合わせをしています。
この記事では、scipy.stats の t.interval() を利用して95%信頼区間の実現値を算出します。
引数 confidence に信頼区間の0.95を指定します。
### 155ページ 続き 他の方法で母平均の95%信頼区間の実現値の算出
# scipy.statsを利用。なおstats.sem()は標準誤差算出関数
stats.t.interval(confidence=0.95, df=n-1, loc=rnd.mean(), scale=stats.sem(rnd))【実行結果】
上の95%信頼区間の下限・上限は合っています!


■ 母分散未知、95%信頼区間が母平均を含む割合をシミュレーション
遂に目的地のシミュレーションにたどり着きました。
母集団分布が母平均 50、母標準偏差 10 の正規分布から標本(乱数)を 15個サンプリングして標本平均を算出する、これを10000回繰り返して標本平均を10000個取得します。
10000個の標本平均の1個ずつ95%信頼区間の実現値を算出して母平均 50 を含むかどうか判定し、最終的に母平均を含む割合を計算します。
95%信頼区間が母平均を含むかどうかの判定には以下の式を利用しています。
$$
T_{0.025} \leq \cfrac{\bar{X }- \mu}{U/\sqrt{n}} \leq T_{0.975}
$$
### 156ページ 信頼区間の実現値が母平均を含む比率をシミュレーション
## 設定と準備
n = 15 # サンプルサイズ
mu = 50 # 母平均
sigma = 10 # 母標準偏差
iter = 10000 # 標本を得る回数(標本数)
## シミュレーション
# 10000個の標本平均(n=15)を取得
rng = np.random.default_rng(seed=123)
rnd = np.array([rng.normal(size=n, loc=mu, scale=sigma) for _ in range(iter)])
# t統計量の算出
t = (rnd.mean(axis=1) - mu) / (rnd.std(ddof=1, axis=1) / np.sqrt(n))
# 95%信頼区間の実現値がt統計量を含む数をカウント
true_num = ((stats.t.ppf(q=0.025, df=n-1) <= t)
& (t <= stats.t.ppf(q=0.975, df=n-1))).sum()
## 結果
true_num / iter【実行結果】
おおむね95%の割合で母平均を含んでいました!


4.2.3 標本平均の区間推定における注意点
■ サンプルサイズが小さい場合の信頼区間シミュレーション
母平均の区間推定にt分布を利用する場合、「統計量$${T}$$がt分布に従うためには標本平均が正規分布に従う必要があります」とテキストは警鐘を鳴らしています。
標本分布が正規分布に従うケース
・母集団分布が正規分布であるとき
・サンプルサイズが十分大きいとき
サンプルサイズが小さい時、t分布に依拠すると信頼区間はどうなってしまうのでしょう!?をシミュレーションします。
母集団分布が平均 0、標準偏差 1の正規分布のケースと、母集団分布が自由度4のt分布のケースを比較します。
サンプルサイズは 20 です。
### 157ページ 母集団分布が正規分布/t分布のケースの比較
## 設定と準備
n = 20 # サンプルサイズ
mu = 0 # 母平均
nu = 4 # 母集団分布であるt分布の自由度
sigma = np.sqrt(nu / (nu - 2)) # 母標準偏差
iter = 10000 # 標本を得る回数(標本数)
## シミュレーション
rng = np.random.default_rng(seed=5)
## 母集団分布が正規分布のケース
# 10000個の標本平均(n=20)を取得
rnd = np.array([rng.normal(size=n, loc=mu, scale=sigma) for _ in range(iter)])
# t統計量の算出
t = (rnd.mean(axis=1) - mu) / (rnd.std(ddof=1, axis=1) / np.sqrt(n))
# 95%信頼区間の実現値がt統計量を含む数をカウント
true_num_normal = ((stats.t.ppf(q=0.025, df=n-1) <= t)
& (t <= stats.t.ppf(q=0.975, df=n-1))).sum()
## 母集団分布がt分布のケース
# 10000個の標本平均(n=20)を取得
rnd = np.array([rng.standard_t(size=n, df=nu) for _ in range(iter)])
# t統計量の算出
t = (rnd.mean(axis=1) - mu) / (rnd.std(ddof=1, axis=1) / np.sqrt(n))
# 95%信頼区間の実現値がt統計量を含む数をカウント
true_num_t = ((stats.t.ppf(q=0.025, df=n-1) <= t)
& (t <= stats.t.ppf(q=0.975, df=n-1))).sum()
## 結果
# 母集団分布が正規分布のとき、95%信頼区間が母平均を含んだ割合
true_num_normal / iter【実行結果】
母集団分布が正規分布のケースでは、95%信頼区間が母平均を含んだ割合は 95% に近似しました。

### 158ページ 続き
# 母集団分布がt分布のとき、95%信頼区間が母平均を含んだ割合
true_num_t / iter【実行結果】
母集団分布がt分布のケースでは、95%信頼区間が母平均を含んだ割合は 95% を上回りました(小さくない差です)。
サンプルサイズが小さい場合、t分布を用いた信頼区間の算出には注意が必要そうです。

■ 別例:母集団分布が非正規分布&サンプルサイズ小の信頼区間シミュレーション
母集団分布が自由度4の$${\chi^2}$$分布の場合にサンプルサイズが小さいケースをシミュレーションします。
自由度4の$${\chi^2}$$分布の期待値は4、分散は8です。
自由度4の$${\chi^2}$$分布の確率密度関数を可視化します。
### 158ページ 自由度4のχ²分布の描画 159ページ図4.20
line_x = np.linspace(0, 30, 1001)
plt.plot(line_x, stats.chi2.pdf(line_x, df=4))
plt.xlabel('x')
plt.ylabel('density');【実行結果】
左側に偏った分布形です。

ではシミュレーションです!
サンプルサイズは 20 です。
### 159ページ 自由度4のχ²分布のケース
## 設定と準備
n = 20 # サンプルサイズ
gamma = 4 # 母集団分布であるχ²分布の自由度
mu = gamma # 母平均
iter = 100000 # 標本を得る回数(標本数)
## シミュレーション
rng = np.random.default_rng(seed=5)
# 100000個の標本平均(n=20)を取得
rnd = np.array([rng.chisquare(size=n, df=gamma) for _ in range(iter)])
# t統計量の算出
t = (rnd.mean(axis=1) - mu) / (rnd.std(ddof=1, axis=1) / np.sqrt(n))
# 95%信頼区間の実現値がt統計量を含む数をカウント
true_num_chi = ((stats.t.ppf(q=0.025, df=n-1) <= t)
& (t <= stats.t.ppf(q=0.975, df=n-1))).sum()
## 結果
# 母集団分布がχ²分布のとき、95%信頼区間が母平均を含んだ割合
true_num_chi / iter【実行結果】
この母集団分布が$${\chi^2}$$分布のケースでは、95%信頼区間が母平均を含んだ割合は 95% を大きく下回りました。

今回の写経は以上です。
シリーズの記事
次の記事
前の記事
目次
ブログの紹介
note で7つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
Python、EXCELのサンプルコードの配布もあります。
2.実験!たのしいベイズモデリング1&2をPyMC Ver.5で
書籍「たのしいベイズモデリング」・「たのしいベイズモデリング2」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは R言語+Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう!
3.実験!岩波データサイエンス1のベイズモデリングをPyMC Ver.5で
書籍「実験!岩波データサイエンスvol.1」の4人のベイジアンによるベイズモデルを PyMC Ver.5で描いて分析します。
この書籍はベイズプログラミングのイロハをざっくりと学ぶことができる良書です。
楽しくPyMCモデルを動かして、ベイズと仲良しになれた気がします。
みなさんもぜひぜひPyMCで動かして、一緒に遊んで学びましょう!
4.楽しい写経 ベイズ・Python等
ベイズ、Python、その他の「書籍の写経活動」の成果をブログにします。
主にPythonへの翻訳に取り組んでいます。
写経に取り組むお仲間さんのサンプルコードになれば幸いです🍀
5.RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析をPythonとPyMC Ver.5 で実践します。
この書籍には時系列分析のテーマが盛りだくさん!
時系列分析の懐の深さを実感いたしました。
大好きなPythonで楽しく時系列分析を学びます。
6.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
統計・データサイエンス書籍にまつわる記事が多いです。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
7.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。
最後までお読みいただきまして、ありがとうございました。
