
小5下第14回 立方体・直方体の切断 学習ポイント
第14回は立体図形の切断です。
3次元でイメージするのは難しいと思われがちですが、正面や上の方向から2次元で切断面を見るところから手順を踏んで丁寧に練習すると理解できます。
何度も練習して慣れると、立体図形に素早く線を描けるようになります。
今回は切断面を描くことに焦点を当ててnoteを書くことにします。
切断後の体積を求めるにも、まずは正しく切断面を描けるようになることです。
切り口の作図のポイント
作図手順の確認です。①→②→③の手順で行います。
①同じ面にある点は結ぶ
②平行な面の切り口は平行
③線を延長して交点をつくる
問題を見ながら確認していきます。
例1(2)
①PとQ、QとRを結びます。
②辺QRに平行な線は赤色のようになります。

この赤色の線ですが、奥の面をイメージして引きづらい方は、正面から見た2次元の図を描いてください。
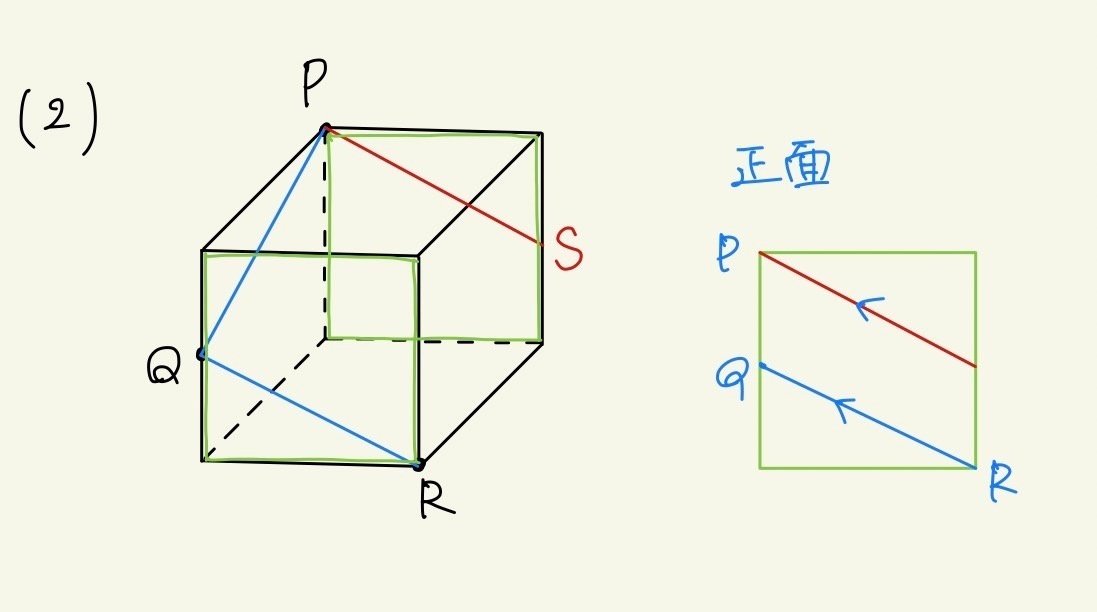
同様に横から見た図も描きます。切り口が完成しました。

※このような切り口は間違いです!
切り口は立体の表面にできますから、立体の中を通ってはいけません。

切り口の形を考えます。
それぞれの直線の長さは全て等しいので、正方形もしくはひし形です。
正方形かひし形かの違いは対角線の長さです。
辺PRは辺QSより長いです。
辺QSと同じ長さは辺PTで、辺PRは立体の対角を結んでいるので長いです。
なんとなく、正方形っぽい、ひし形っぽいではなく、根拠を説明できると、間違ってるかも…と不安になりながら解答することがなくなります。

例1(3)
①PとQ、QとRを結びます。
②次に、平行な面には平行な直線を引くというところですが、この後、辺PQに平行な線を引くの?辺QRに平行な線を引くの?と迷うことがあるかもしれません。
点Pか点Rを通る線を引いてください。

つまり、引けるのは辺PSです。
辺PQがある面と平行な面には点がないので線は引けません。

切り口は台形です。

例題2
立体のままで考えるのが難しい場合は、とにかく丁寧に、平面図を描きながら進めます。
①CとQを結びます。

②辺CQと平行に点Pから平行線を引きます。
横から見た図を描くと、辺の比も一目瞭然です。
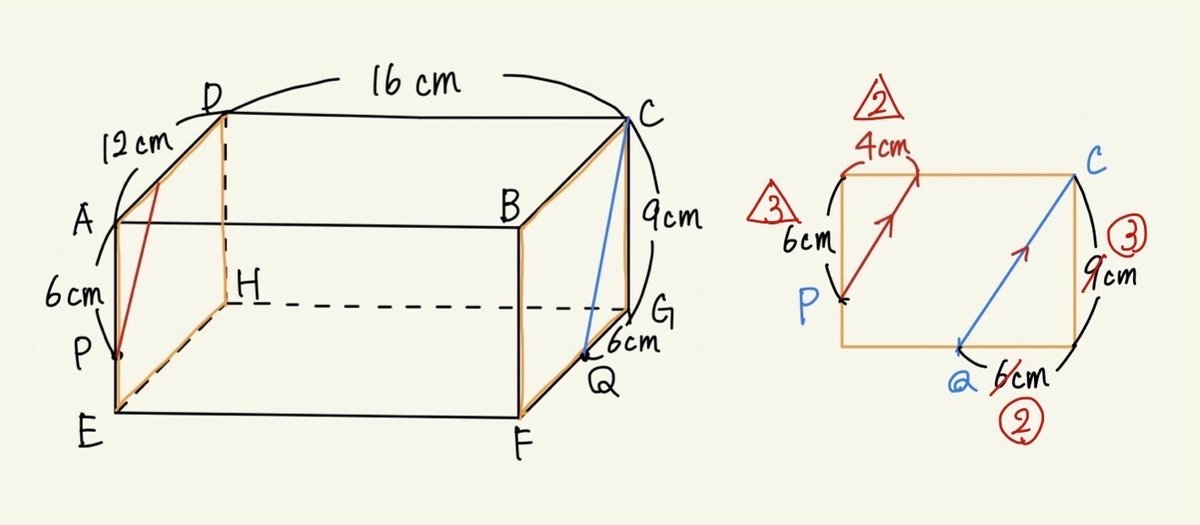
新しくできた辺AD上の点RとCを結びます。

先ほどと同じようにして、点Qを通る、辺RCに平行な線を引きます。
最後、点Pと結んで完成です。

例題3
難関校対策とありますが、立方体の切り口の問題としては優先度が高い問題です。
作図のポイント3番目の、線を延長して交点をつくるが必要なパターンです。
1.辺PQを作って、平行な辺RSを描きます。

2.線をのばす際、どこに向かってのばすか分かりやすくするためにかべを描きます。
立方体を部屋のすみっこに置くイメージで、立方体の辺を延長してかべを作りましょう。

3.辺RSをかべの線に向かってのばします。そして、交点を作ります。

4.交点がそれぞれ点P、点Qと同じ面にできたので、結びます。

5.もとの立体の交点と点R、点Sをつないで完成です。
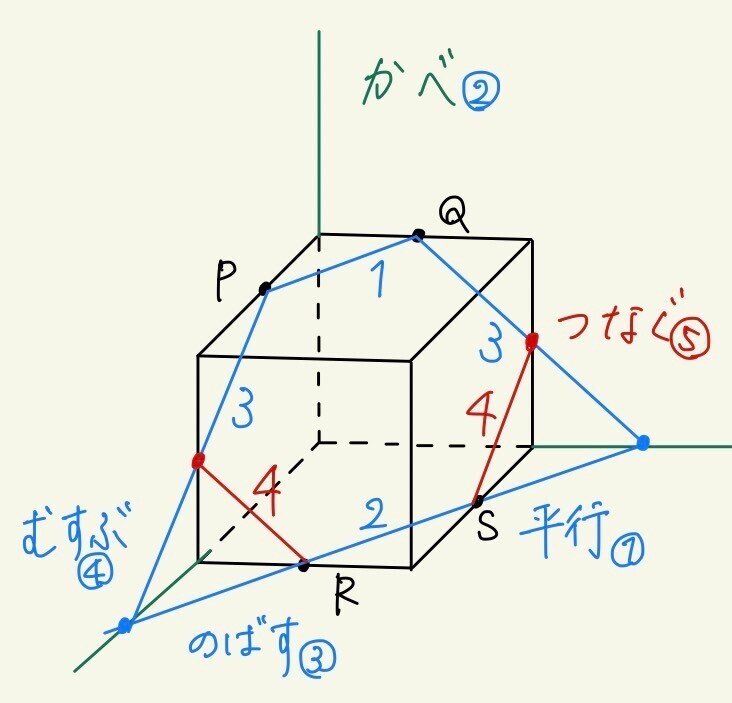
次に何をするの?と思考が止まらないために、手順の呪文を唱えて口で覚えると効果的です。
1平行→2かべ→3のばす→4むすぶ→5つなぐ
慣れると動画のようにすらすら描けるようになります。
立体図形の切断を立体のままで考えられるのは、Sコース生、Cコース上位生、ABコースで普段からプラモデルや積み木など立体に触れている方という印象です。
立体図形の問題や3次元の世界にどれだけ馴染みがあるかで解きやすさが左右されるので、馴染みのない方はこれから毎日紙の上で立体を切って、それを脳内でイメージすることを続けてください。そうすると2週間もすれば頭の中で立体が切れるようになります。
演習問題集のp.104 反復問題(基本)大問1、p.108〜109 トレーニング 大問1、2を速く正解できるまで練習してください。
また、図形断面図を確認できる立方体の切断の攻略 (受験脳を作る)もおすすめです。
立体図形切断の特訓プリントなどで練習することも進めていきます。


告知
ドリるゼミでは、予習シリーズの各単元の内容に合わせた導入授業を行なっております。(教材は、オリジナルプリントです。)
ドリるゼミ月会費・・・990円(税込)/月 (教材・システム・コミュニティー運用などの費用)
授業料・・・2500円(税込)/1回 (参加した回数分のお支払い)
お申し込みはドリさん(Twitter)or (公式LINE) へメッセージお願いいたします。
詳細は、こちら
最後までお読みいただき、ありがとうございました。
文責: かやもり(https://twitter.com/kayamoriedu)
