
第10回組分け対策後半 (第6〜9回まとめ②)
前回は第6回速さと比、第7回旅人算の比について、入試や組分けテストでよく出る問題について書きました。
今回は第8回平面図形と比、第9回図形の移動について最低限おさえておきたい問題についてお話します。
ここで、一度告知させていただきます。
11月6日 日曜日 10:00 ~ 12:00に、ドリるゼミ組分け対策勉強会を行います。偏差値 45 ~ 60くらいが目安です。オリジナルプリントを用いて第6〜9回の範囲を満遍なく復習します。詳細は、こちら
第8回の最低限おさえておきたい問題
以下の4つです。
例1 三角形の面積比を使った問題
例2 補助線を引いて相似の三角形を作る
例4 ベンツ切り
例5 正六角形の分割
例1 三角形の面積比を使った問題
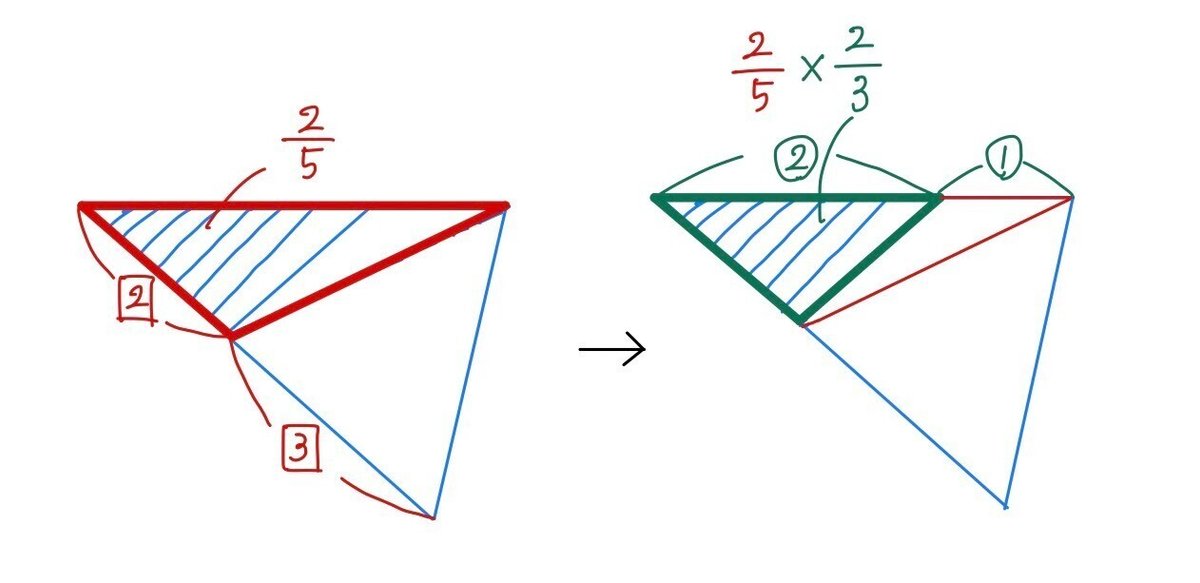
解き方としては、平行四辺形は全体の何分のいくつ→三角形は平行四辺形の何分のいくつと順を追って求めます。

緑の三角形が青い三角形の何分のいくつかを求める方法を忘れるお子様が多いのですが、青の三角形→赤の三角形→緑の三角形と範囲を狭めていくと求まります。


例1のつまずきポイント
ステップ②で、赤い三角形は青い三角形の何分のいくつ?という考え方が難しいというお子様がいらっしゃいます。
「高さが等しい三角形の面積比は、底辺の比と等しい」という考え方に慣れていないことが原因だと思われます。
その場合は、以下のような問題の練習に数多く取り組むと慣れてきます。

例2 補助線を引いて相似の三角形を作る
相似形を作るために補助線を引くという思考回路を身につけます。

相似に慣れていない方は、ピラミッド型の相似比を間違えることがあります。不安がある場合は、第2回の範囲で、例1(三角形の相似 〜クロス型とピラミッド型〜)の問題を復習してみてください。

例4 ベンツ切り
ベンツの形に区切って、3つの三角形の面積比を、2つずつ連比をとって求めます。
常に「底辺の比=面積比(高さが等しい三角形の面積比は、底辺の比と等しい)」を意識して図形の問題に取り組めるようになるといいですね。


例5 正六角形の分割
兎にも角にも頻出問題なのですが、触れる機会が少ないため苦手意識のあるお子様が多い印象です。
たくさん問題を解いて、一度慣れてしまえば、基本問題は正解できるようになります。

↑このような問題が演習問題集 p.62トレーニング[2]にありますので、演習問題集をお持ちの方は取り組んでみてください。
第9回の最低限おさえておきたい問題
新出範囲の例3(おうぎ形の転がり移動)と例4・5(図形の平行移動)です。
例1と例2は復習範囲ですが、頻出問題で6年生になっても学習するので、時間があれば復習することをおすすめします。
解き方とつまずきポイントはこちらの記事をご覧ください。
最後までお読みいただき、ありがとうございました。
ドリるゼミスタッフ 栢森(@kayamoriedu)
