
小5下第13回 整数の分解と構成 学習ポイント
第13回では、素因数分解や約数の個数の求め方、わり切れる回数などを学習します。
夏期講習で少し触れた単元でもあります。
理屈が理解できない、何をやってるかわからない、というお子様も多いですが、そんなものです。
理解できる範囲の解き方から始め、解き方を身につけていきましょう。
それでは、各例題のポイントです。
例1
素因数分解の問題ですね。
連除法と同じように割り算の筆算を逆にしたような書き方をして解くように解説があります。が、あまりお勧めしません。
かけ算に分解するというイメージでこういうふうにやってみましょう。

連除法だと、作業になってしまいがちです。
この方法で繰り返してると、数のイメージが湧きやすくなり暗算でも解けるようになってきます。
素因数分解のドリルというサイトで、問題を自動生成してくれるので、お勧めです。
暗算の練習・スピードをチェックしたい方は、ドリる算数のドリるを用意しております。

上の問題だと、24 = 4×6 = 2×2×2×3 と、頭の中で暗算するイメージですね。
例2
約数の個数を求める問題です。
解説には、素因数分解を利用する解き方が書かれていますが、まずは、約数のペアを作る方法で解けることを確認しましょう。
テストで、「やり方忘れたから解けません!」なんてことがないように。

上記の方法で、求めることができると確認した後、素因数分解をする方法で解けるように練習しましょう。
2×2×2×3×3ではなく$${2^3×3^2}$$とかく方が良いと思います。
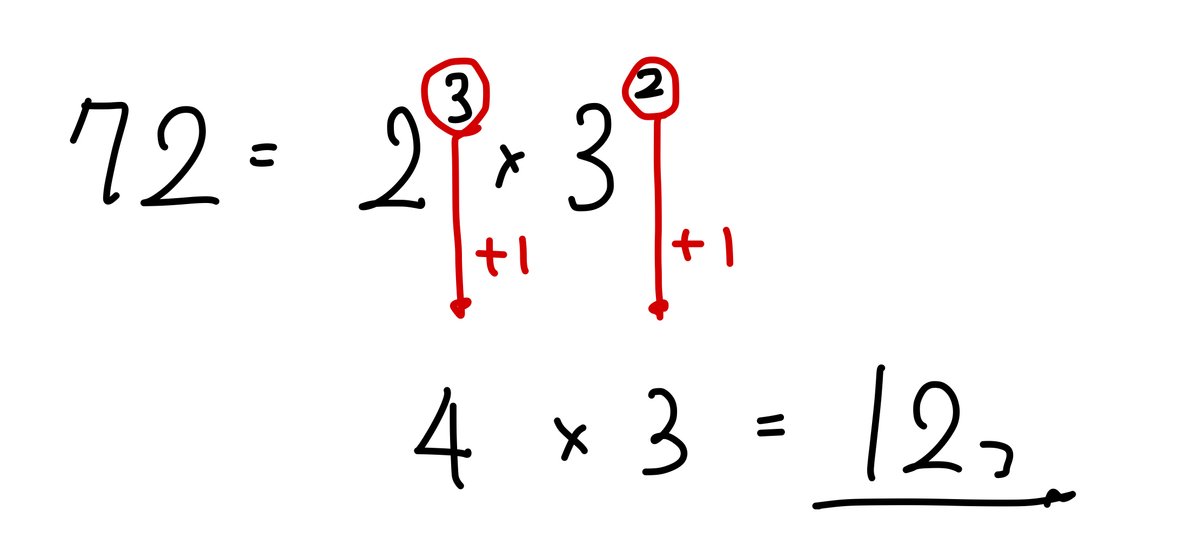
なんで、こうなるの? と疑問に思うお子様も多いです。
そんな時は、
72を素因数分解した「2×2×2×3×3」から一部を取り出したら約数になるよ。例えば、2×3とか。それを2の個数、3の個数に注目して表を書くとこうなるよ。
と説明してみましょう。
すると90%のお子様は「なるほどー(棒読み)」という反応になります。
「本当にわかったの??」と聞かないようにしましょう。
あまり深入りせずなんとなく理解できれば十分です。

逆に、完全に理解するまで納得しないお子様には「60の約数の時はどうなる?」 など、もう少し深く考えても良いですね。
(60は、表では書けなくなるので、別の手段で書くことになります)
例3
理屈は、予習シリーズの解説が正しいですが、解き方としては以下の考え方が理解しやすいと思います。
「5の倍数ということは、5×??となるので、300を5で割った60の約数を考えましょう。」
なんで、こうなるの?と疑問を持つお子様には、300の約数のうち5の倍数を書き並べ、5×(60の約数)になってることを確認しましょう。

最悪、300の約数を全て書き出して5の倍数を数えても…解けますので、解き方を忘れた場合の最終手段として使えるように。
例4
約数の個数が奇数個 → 平方数
約数の個数が3個 → 素数の平方数
ということを、押さえればひとまずOKです。
約数が4個の場合は…予シリの解説通りです。
が、ちゃんと理解してもらうのは難しいですね…。
算数が苦手なお子様は一旦飛ばしてもOKです。
例5,6
こちらは予シリの解説通りで解ければOKです。
例7
解き方は簡単なのですが、最短の解き方しかわかってないと、何をやってるのかわからなくなります。
割り続ける → 約分し続ける
と考えて、約分しまくってみましょう。

上のように考えると、割る回数 = 約分する回数と捉えられます。
(2)は、0が何個続くか。→ 10で何回割れるか。→(2×5)のセットを何個約分できるか→結局5で何回約分できるかを考えたら良い。
という流れで考えます。
告知
ドリるゼミでは、予習シリーズの各単元の内容に合わせた導入授業を行なっております。(教材は、オリジナルプリントです。)
ドリるゼミ月会費・・・990円(税込)/月 (教材・システム・コミュニティー運用などの費用)
授業料・・・2500円(税込)/1回 (参加した回数分のお支払い)
お申し込みはドリさん(Twitter)or (公式LINE) へメッセージお願いいたします。
詳細は、こちら
最後までお読みいただき、ありがとうございました。
文責: ドリさん
