
Pythonで数学をやってみよう!- オイラーのγの近似値 2 - 数列の和を求める。
調和数列(ちょうわすうれつ、harmonic sequence または harmonic progression)とは、各項の逆数を取ると等差数列となる数列である。ピタゴラス音律では、ドの弦の長さを 1 とすると、ソは 2/3、1オクターブ高いドは 1/2 の長さになる。各項の逆数はそれぞれ 1, 3/2, 2 となり、公差が 1/2 の等差数列となる。よって、1, 2/3, 1/2 は調和数列である。
数列の和を求めるプログラムを見ていきます。等差数列や等比数列の第n項までの和を求める場合は公式が使えるので、単純にそれらの公式を使って計算すれば済みます。なお、数列の和のことを級数と呼ぶこともあります。
コードを書いて実行してみます。
調和数列の和
def sumharmonic(m):
sum = 0
for k in range(1,m+1):
sum += 1/k
return sumと定義して、
sumharmonic(100)としてやれば合計が出ます。
オイラーのγの近似値
調和数列の和は、mの値をどんどん大きくすると、無限大に発散することが分かっています
プログラムで無限に足し算を行うことはできないので、近似値を求めるためにmに好きな値を指定して計算できるようにしましょう。
lnというのはlog n ということで、
import math
def sumharmonic(m):
sum = 0
for k in range(1,m+1):
sum += 1/k
return sum - math.log(m)return sum - math.log(m)
sumからmath.log(m)を引き算します。logを使うためにmathをimportしてからコードを書きます。
ネイピア数(e)の近似値を求める
ネイピア数(自然対数の底e=2.71828...)を求めていくのですが、そもそも対数とは、
ネイピア数とは、
今回提示してあるコードです。公式をコードに。
import math
def myexp(n):
sum = 0
for i in range(n):
sum += 1 / math.factorial(i)
return sum公式
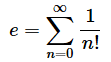
スタートはn=0、そこから順に足していきます。何を足すかというと
n!
“!“がつけると階乗という意味になるため、
Pythonでは関数factorial()を使って表現し、必要な算術式は
1 / n!
で、これを公式では連続的に足していく(シグマ)操作をしているので
for i in range(n):
sum += 1 / math.factorial(i)for in 文を使って連続的に足して、変数sumに追加します。
それでは
myexp(10)として実行します。
2.7182815255731922
と答えが出てきます。
Σの計算はコードではfor in文で実装できます。その取り出した数字を公式の計算式に適応し、順次足していきます。
