
統計|時系列データから因果関係に迫る―手順編―
以前,交差遅延効果モデルについて概要と媒介分析を説明をした記事を書いた。今回は書こうと思いつつもしばらく放置していた続きの内容。
交差遅延効果モデルを分析するまでの手順をメモしてみた。
交差遅延効果モデルの手順
手順としては以下の通り。
記述統計と信頼性係数を算出する。
脱落者(欠損データ)の分析をする。
全変数で相関分析をする。
各尺度の因子分析(CFA)をする。
交差遅延効果モデルを作って分析する。
制約をかけてみる。
媒介分析をする。
1.記述統計と信頼性係数を見る
ここは特に言うまでもないと思う。信頼性係数については α,ω を出す。再検査信頼性を記載している論文もあったりする。とはいえあとで相関分析するので,再検査信頼性として書く必要は特にないかな。
2.脱落者(欠損データ)の取り扱い
縦断調査なのでもちろん脱落者が出てくる。各調査時点の脱落者と最後に残った分析対象者の得点を比較して,脱落によるモデル検討への影響がないか
調べている研究もある。
いろんな方法があるらしく,「Missing data analysis」,「Preliminary analysis」みたいに項目立ててある論文なんかは要チェック。以下,例を2つ挙げる。
・Datu & King(2016) Time 3 まで調査
データが揃っている人と揃っていない人で,Time 1 の得点の平均値の差を検討した結果,p = 0.05, multivariate η² = 0.19 だったため差がないとして扱っている。
・Geibel et al.(2022) Time 3 まで調査
T2 まで完了の人と T1 だけの人で年齢,性別,所属グループ規模を比較。T3まで完了の人と T2 まで完了の人で複数変数を比較(t 検定)。なぜ分散分析ではない?と思ったけど T2 ― T3 からはフェイスシートだけでなく尺度得点の分析も含めて分析したからかな。
あとどの論文だか忘れたけど,3波の調査をして,1~2回目の脱落者と2~3回目の脱落者と3回目に残った人の得点(1回目の得点)で分散分析をして,有意でなかった場合は影響なしとするというようなのもあったはず…。見つけたら追記する。
他にもロジスティック回帰分析を使う方法もあるみたいで(Bergen-Cico & Cheon, 2014),手法が確立されているわけではないっぽい?
難しい!
3.全変数で相関分析をする
交差遅延効果モデルは SEM を使った分析をするわけだが,SEM を行う場合,登場する変数はなんかしらの関連(相関)があることが分かっているうえで分析する必要がある。つまり事前分析として相関分析を行わなければならない。
相関分析は各変数の Wave 1~3 における全ての得点を相関分析する。基本的には各 M,SD と相関係数を書くけど,α 係数も書いている論文もある。
Table の書き方は Bergen-Cico & Cheon(2014)のような尺度ごとでまとめているものや,Hakanen & Schaufeli(2012)のようにTimeごとにまとめているものがある。α 係数も書いてあるのは Datu & King(2016),Ma(2019)など。要は下の図のような感じ。


ちなみに概要編で紹介した,西田他(2014)では Wave 1 における各変数の得点のみを相関分析している。
自分が見た範囲内だけど全観測時点の得点で相関分析をしているものがほとんどかな。図がでかくなってしまうけど,手順1でも触れた再検査信頼性も確認できるので基本的には全観測時点で分析が必要かと思う。
4.各尺度の因子分析(CFA)をする
ここでは,各測定時点における尺度の測定不変性を検討する。
これもまたやり方がいくつかあるらしく,各時点でそれぞれ確認的因子分析(CFA)をして適合度の比較をしている研究や(Burić & Macuka, 2018),縦断的 CFA を行っている研究もある。
縦断的 CFA は,尺度開発の因子的妥当性の検証で行うような1時点測定のデータからの分析を,複数時点測定で分析するものである。分析は SEM で行い,各測定時点で同じ項目にささっている誤差変数同士と,各測定時点の概念の潜在変数同士を共分散でつなぐというもの。
そしてモデル適合度を確認して基準を超えていたら測定不変性が担保されていると言える。以下に図を入れて見たけどこれでイメージできるだろうか…。
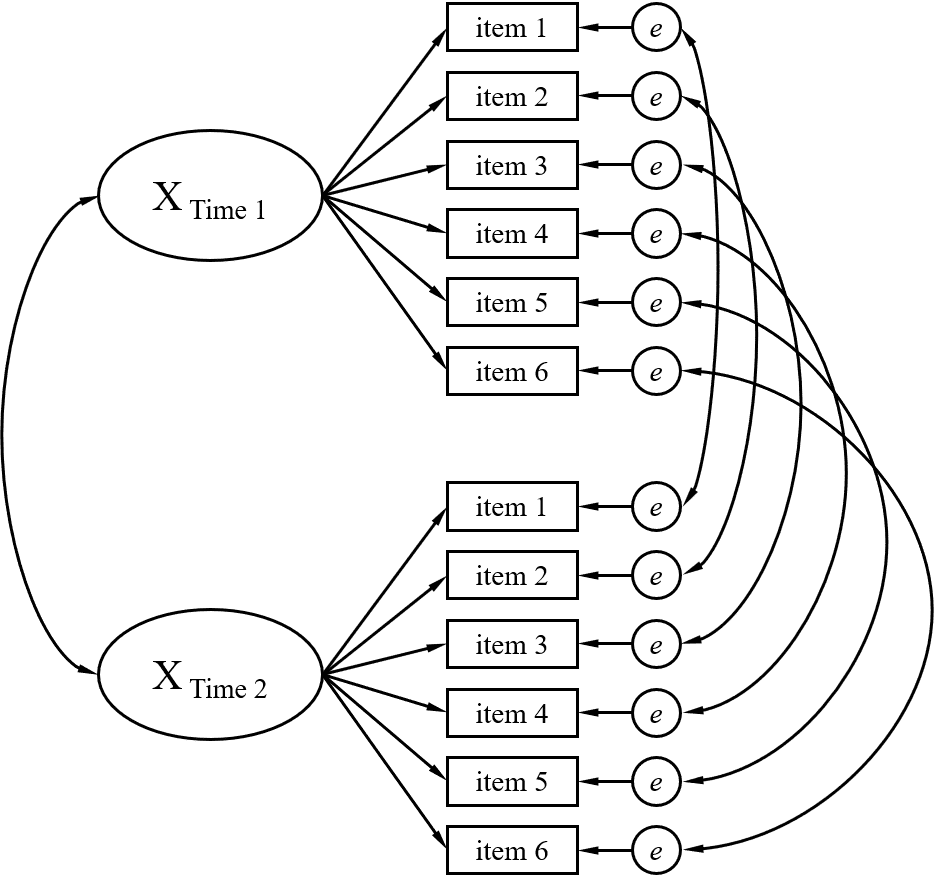
この図では見やすいように 1 因子 6 項目としたが,現実はそううまくいくわけもなく,複数因子で 20 ~ 30 項目なんてこともよくある。自分の博論では 4 因子 21 項目の尺度を使って結構困ったんだけど,2 次因子構造の尺度だから各因子得点をパーセルとして扱って分析した。(20 項目以上の尺度でしっかりモデル作ると線まみれでかなりキモい図になるので是非)
ちなみに縦断的 CFA の日本語文献は見当たらず,以下の英語論文が役に立った。
Goodman-Williams & Ullman(2020)
Torréns & Kärtner(2017)
Urbán, Szigeti, Kökönyei, & Demetrovics(2014)
(理解できている自信はない)
5.交差遅延効果モデルを作って分析する。
モデル分析についてはこれまでの概要編と媒介編で説明してあるので省略。
6.制約をかけてみる。
交差遅延効果モデルでは,制約というものをかけて分析することがある。
制約とは,
共分散構造分析で推定する母数(パラメータ)がこれら「分散」「共分散」「係数」であり,特に何も指定しなければ全てラベルなしの自由母数として推定されることになります。ただ,分析者の推定する母数同士の関係をモデルに導入することもでき,これを母数の制約と言います。
また,母数(パラメータ)同士で値が等しいという制約を置くことを等値制約という。
制約はかけている研究とかけていない研究どちらもあるので,これは扱う概念や検討したいパスによって判断するべきなのかな。ここは全然理解できている気がしないので,間違ったことを書かないよう浅くメモする。取り扱うのは概要編,媒介編でも紹介した日本語論文(西田他,2014;島本・石井,2010)。
「高齢者における知能と抑うつの関係」
西田他(2014)では,双方向の因果関係を示す「Full」モデルと,「知能→抑うつ」モデル,「抑うつ→知能」モデルの3つを検討している。
Full モデルでは,「抑うつ」→「知能」と「知能」→「抑うつ」 の
どちらのパスも含まれたモデル,要は概要編の記事で説明した交差遅延効果モデルのベースとなるモデルで検討している。
続いて「知能→抑うつ」モデルでは,「知能」から「抑うつ」の影響を比較するために,「抑うつ」から次時点の「知能」へのパス係数を0として制約を課し,「知能」から次時点の「抑うつ」の係数のみを推定した。
その際,「知能」→「抑うつ」の Wave 1 → Wave 2,Wave 2 → Wave 3 に等値制約を課し,以上のパスが同等であると仮定している。
「抑うつ→知能」モデルは逆のことをやっている。
「運動部でのスポーツ経験とライフスキルの関係」
島本・石井(2010)では,
・1時点目から2時点目,2時点目から3時点目の交差遅れ効果と,安定効果はそれぞれ等しい
・2時点目と3時点目における誤差共分散は等しい
という等値制約を課している。
こういった感じで研究によってはパスに制約をかけており,検討したい関係性を見出すには制約を使いこなす必要がある。
ちなみに Amos で制約をかける場合,川端(2007, pp. 86–87)の説明が分かりやすい。
ざっくり説明すると,各パスを右クリックしてパラメータに名前を付け,「分析」→「モデルを管理」で出てくるウィンドウの「モデル名」ボックスに○○モデルと名付ける。その下にある「パラメータ制約」ボックスに等値制約をかけたいパスを "=" で結ぶ,もしくは "=0" とする。
例えば,以下のモデル図だったとする。
(島本・石井(2010)を参考にした)

西田他(2014)のようにX→Yの影響を検討する考える場合,Y→X を0とするため,b=0,g=0 をボックスに入力する。さらに各測定時点の等値制約をかけるため,c=h,d=i をボックスに入力する。
島本・石井(2010)のように同じ方向の交差遅延効果と安定効果に等値制約をかける場合,a=f,b=g,c=h,d=i を入力する。また,誤差共分散の等値制約は e=j を入力する。
7.媒介分析をする。
研究目的に応じて媒介分析を行うこともある。詳しい説明は前回記事の媒介編で説明してあるので省略。Amos で媒介分析を説明した記事もあるので,たぶん参考になるかもしれない。記事のリンクは下の方に貼っておく。
おわりに
交差遅延効果モデルの分析手順をメモしてみた。文が粗いし明らかに説明を逃げているところがあるのであとで直すかもしれない。
媒介編の媒介分析の記事を投稿した時に「3.相関分析をする」のとこまで書いてあったが,それから放置し続けて1年以上経ってしまった。概要編,媒介編を書いてた時の方が記憶が新鮮なので,正直今回は間違えまみれなんじゃないかとけっこう不安を抱えている。いや概要編,媒介編も不安か…。
それから,交差遅延効果モデルの記事はこれで終わりになる。ここまで書いて,そして自分のデータで分析してみて思うこととしては,まだまだ研究蓄積やガイド的なものが少ないため,実際にやってみるといろいろな壁にぶつかる分析だった。まあそれは自分の知識が足りないだけかもしれないけど。ただ,面白い分析ではあるので,向き合ってみる価値はあったと思う。
あとこの流れと関係ないけど,今回の記事(③)書いて思ったのは,内容的には①→③→②(概要→手順→応用(媒介分析))の方がわかりやすいかもしれない。さらに記事タイトルは①②③とかじゃなくて○○編とかにした方が見やすかったかもしれない。という反省。○○編に名前変えました。(2023年8月27日)
いつも書いているけど統計が苦手なので,詳しい方は間違いを見つけ次第,是非ご指摘お願いします。ただ,ご指摘を理解できるかわからないので易しめかつ優しめでお願いします。
以前の記事はこちらから。
引用はさらに下部にあります。
SEM のモデル適合度に関する記事もアップしています。
< 文献 >
Bergen-Cico, D., & Cheon, S. (2014). The mediating effects of mindfulness and self-compassion on trait anxiety. Mindfulness, 5(5), 505–519.
https://doi.org/10.1007/s12671-013-0205-y
Burić, I., & Macuka, I. (2018). Self-efficacy, emotions and work engagement among teachers: A two wave cross-lagged analysis. Journal of Happiness Studies: An Interdisciplinary Forum on Subjective Well-Being, 19(7), 1917–1933. https://doi.org/10.1007/s10902-017-9903-9
Datu, J. A. & King, R. B. (2016). Prioritizing positivity optimizes positive emotions and life satisfaction: A three-wave longitudinal study. Personality and Individual Differences, 96, 111–114.
https://doi.org/10.1016/j.paid.2016.02.069
Geibel, H. V., Rigotti, T., & Otto,K. (2022). It all comes back to health: A three-wave cross-lagged study of leaders' well-being, team performance, and transformational leadership. Journal of Applied Social Psychology, 52(7), 532–546. https://doi.org/10.1111/jasp.12877
Goodman-Williams, R., & Ullman, S. E. (2020). Posttraumatic stress disorder and measurement invariance in a sample of sexual assault survivors: Are symptom clusters stable over time?. Psychological trauma : theory, research, practice and policy, 12(4), 389–396. https://doi.org/10.1037/tra0000509
Hakanen, J. J., & Schaufeli, W. B. (2012). Do burnout and work engagement predict depressive symptoms and life satisfaction? A three-wave seven-year prospective study. Journal of affective disorders, 141(2-3), 415–424.
https://doi.org/10.1016/j.jad.2012.02.043
川端 一光(2007).第4章 多母集団分析 豊田(編)共分散構造分析[Amos編](pp. 73–88) 東京図書
君島 康昭(2007).第2章 上級者への道 豊田(編)共分散構造分析[Amos編](pp. 25–50) 東京図書
Ma, C. M. S. (2019). Relationships between Exposure to online pornography, psychological well-being and sexual permissiveness among Hong Kong Chinese adolescents: A three-wave longitudinal study. Applied Research in Quality of Life, 14, 423–439. https://doi.org/10.1007/s11482-018-9604-5
Torréns, M. G. & Kärtner, J. (2017) Psychometric properties of the early prosocial behaviour questionnaire, European Journal of Developmental Psychology, 14(5), 618–627. https://doi.org/10.1080/17405629.2016.1259107
西田 裕紀子・丹下 智香子・富田 真紀子・安藤 富士子・下方 浩史(2014).高齢者における知能と抑うつの相互関係:交差遅延効果モデルによる検討 発達心理学研究,25(1),76-86.
https://doi.org/10.11201/jjdp.25.76
Urbán, R., Szigeti, R., Kökönyei, G., & Demetrovics, Z. (2014). Global self-esteem and method effects: competing factor structures, longitudinal invariance, and response styles in adolescents. Behavior research methods, 46(2), 488–498. https://doi.org/10.3758/s13428-013-0391-5
