
2021年度第3,4回デジラボ:kerf bendingベンチを作ろう
はじめに
こんにちは。北九州市立大学のM2の齋藤魁利と渡辺哲平、M1の小林広樹、B4の遊佐太貴です。
今回のデジラボでは、kerf bending(living hinge)の切り欠き間隔の最適化を行います.graddhopperのコンポーネント,GalapagosやKangaroo2を用いて最適化を行い,shopbotで実際に製作しました.
kerf bending(living hinge)
唐突ですが,はじめにこの動画をご覧ください.
これはkerf bending(living hinge)といわれる,ある程度の厚さの素材を曲がるように加工するカッティング技法を施した木板です.
この動画をみたらだれでも考えることだと思いますが,私たちも同じで
「触ってみたい」
「どうやって曲がるん?」
「これで何か作れるんじゃない?」
そう思いました.
ここで同時にこう思いました.
「Shopbotあるし,実際にベンチでも作ってみるか!」
少し調べると,実際に作られていました.

こんなねじれた形は自分たちにはまだ早いと,とりあえず1方向に曲がるベンチを作ることにしました.
そこで私たちはkerf bendingについて少し勉強しました.
kerf bendingについて
Nature architects 大嶋さんの論文を読まさせていただき,若干理解したので,かるくリビングヒンジについて説明します.
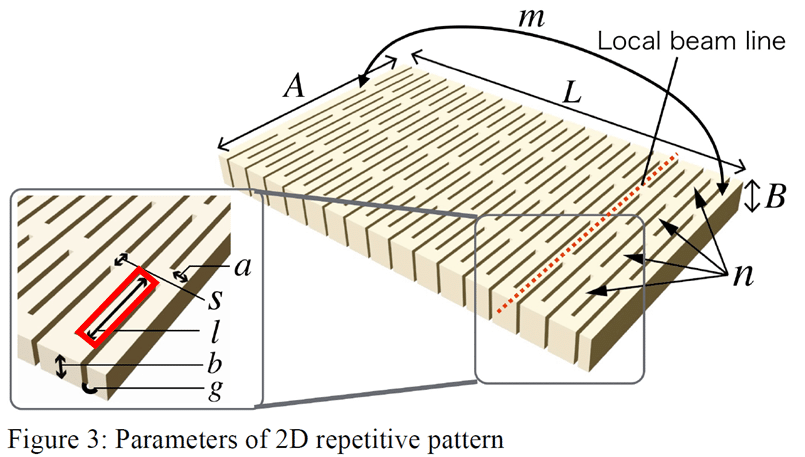
変形角二乗和と最適化

この曲線にフィットさせる中で効率の良い切り欠き方を見つけられないか?という考えのもと最適化をしてみます.
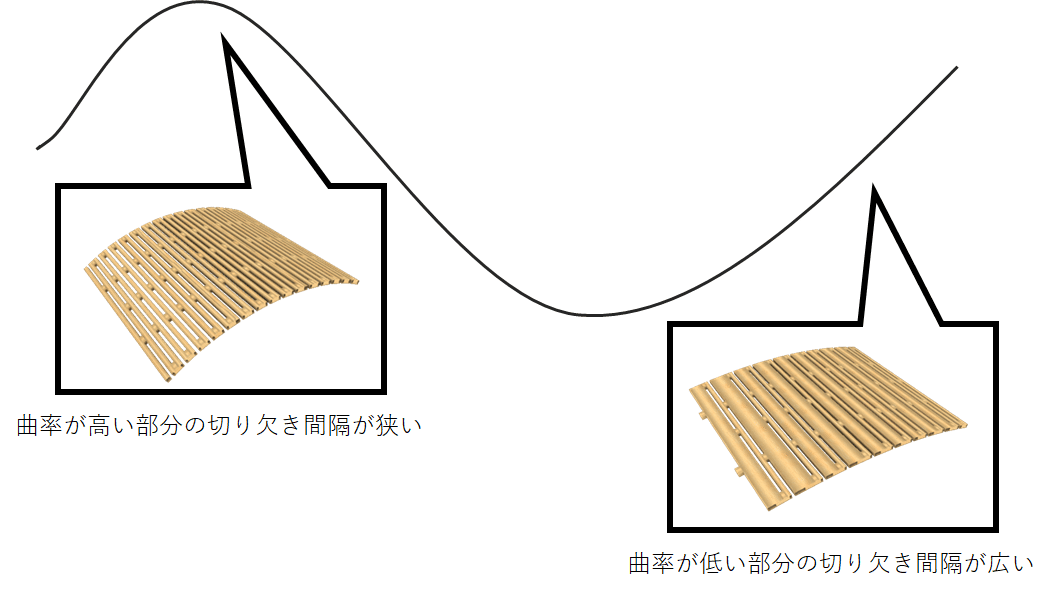
効率の良いとは,
曲率が高い部分の切り欠き間隔が狭く,曲率が低い部分の切り欠き間隔を広くなるような切り欠き方とし,適材適所の柔らかさを持つことだと定義します.
今からはこの曲率に注目して効率の良い切り欠き方を探していきます.
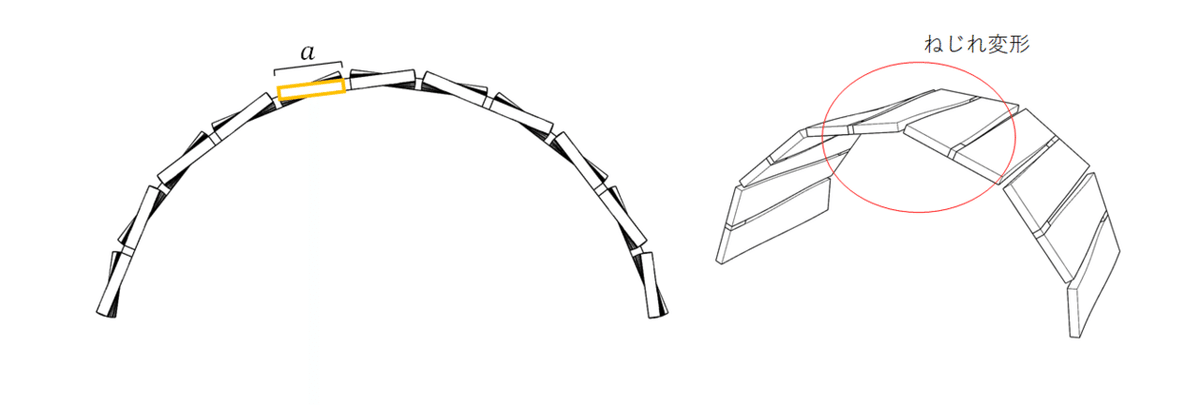
例を挙げます.
ある一定の曲率をもつビームの長さがaのリビングヒンジを考えます.

このようにaを小さくする,つまりビームを密に配置することでねじれ変形θ(ポインタで説明)を小さくしています.
逆に曲率の低い位置はビームを疎に配置し切り欠き数をできるだけ少なくします.

実際にNature architects 大嶋さんの論文中の式から考えてみます.
曲げモーメントは上の式で,曲率φはこのように定義されています.
この曲率φの中にあるねじれの変形角θにフォーカスを当てます.
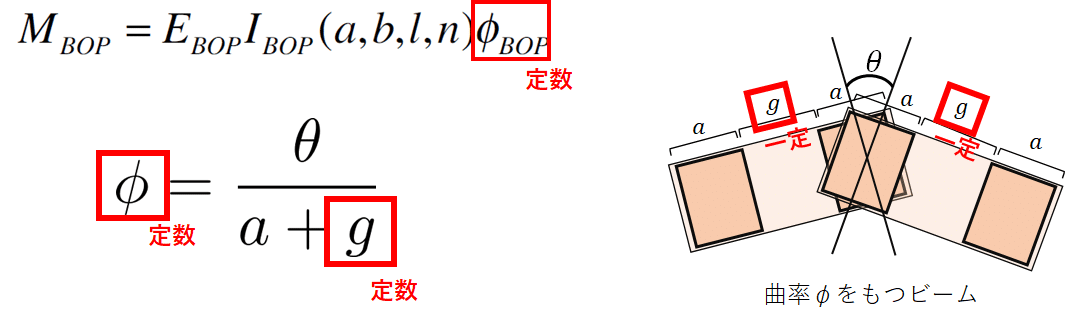
今回のデジラボでは切削加工時間を短縮するため,gをビットの直径で一定としています.
一回の切り欠きパスで切削できるようにしているということです.
曲率φは設計者が直接与える数値なので定数です.

式変形すると,変形θはこのように書けます.
Φとgが一定のときaを小さくすると,ねじれ変形θも小さくなることは明らかです.
また,角度の関係から,各ビームのねじり変形θ(黒θをポイント)と勾配差θが同一のものとなります.
以上のことより
本最適化ではaを設計変数,変形角θの二乗和を目的関数とし最小化を行うことで切り欠き間隔の最適化を行います.

では,なぜ変形角の総和ではダメなのか説明します.
各ビームの変形角θを図に示します.
変形角θは次のように表せます.



今まで述べてきた変形角θは,奥の断面に垂線を引いたものの勾配と,
手前の断面に垂線を引いたものの勾配との差をとったものになります.

ここでシンプルに変形角を総和すると,

このようになりますが,この∑θは実は,

最初の断面と最後の断面の差をとったものと同じ大きさになります.
ここに問題があります.

Θ1,1とθ11,2に注目してみると,

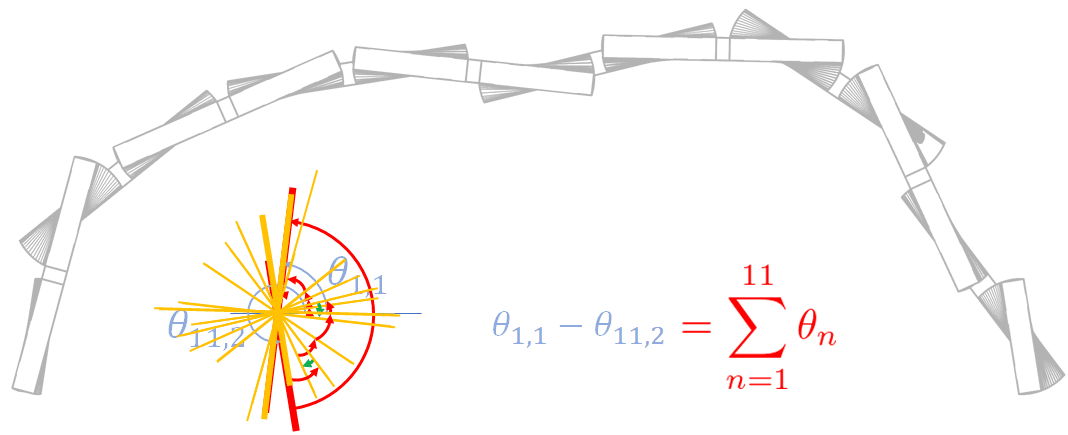
このように曲率が変わったとしても,合計の値が同じになってしまいます.
以上のことが原因で変形角の総和では適切に最適化が行えないと考えられます.
そこで,各ビームの変形角の二乗和を目的関数にすることとしました.
最適化問題の定式化を行っていきます.
最適化問題の定式化

目的関数・・・変形角の二乗和
制約条件・・・使用材料の長手方向長さとビームの幅
を設定しています.
Galapagosで最適化問題を解く際,制約条件をペナルティ関数として定式化を行い,目的関数に足す必要があります.

以上で定式化の説明は終了です.
最適化結果
最適化前

最適化後

Kangaroo Physicsでの解析
初期値はLが制約条件内に収まるよう,38に数値を設定したGene PoolをRandomize 10%にしました.
最適化後は最大の変形角も小さくなり,θiの分布もまとまりつつ,値も小さくなっています.
実際にshopbotで切り出し,製作してみた.
試験的に合板で作ってみました.

上手にフィットしました.
が,一つ問題点

shopbotの切り欠き設定が原因か材料が原因かわかりませんが,剥離が起きました.
ここで,最適化問題の定式化の見直しと使用材料の見直しを行いました.
最適化問題の見直しと使用材料の見直し.
もう一度事例を見直すと,


このように,太いビームと細いビームの交互になっていることに気が付きました.
このようなビーム配置になるよう定式化をし直します.

以上で定式化の見直しは終わります.
最適化結果
最適化前

最適化後

実際にshopbotで切り出し,製作してみた.Part2

使用材料は試作1では割れが発生してしまったため、ベニヤを積層させた合板ではなくMDFを使うことにしました.
kerf bendingの様子
組み立て
組み立て後


この試作では、座面下部材の曲線を座面の曲線より低くし座面を浮かせることで,座面に弾力をもたせ,体へのフィット感を促しています。
まとめ
今回はkerf bendingを使用したベンチを紹介した.
kerf bendingのベンチは変形角の二乗和やMDFを使用することで,目指した変形ができ制作が行えた.
kerf bendingは実施事例が少ないため,様々な使用方法について模索したいと考える.
kerf bendingの使用方法例


kerf bendingの使用方法例として柔らかい木製の椅子を作りました。
この椅子は木のあたたかさを持ち、クッション性を生み出せる椅子となっており、実際に座ってみると変形して体へフィットします。
さらに、押してみると、ばねのように元の形状に戻るようになっております。
動画
今回のデジラボをこちらに上げております。
参考にしたもの
木材がグネグネ曲がるリビングヒンジ特集
SLUSH BENCH
・構造設計:DN-Archi+Nature Architects
・意匠設計:VUILD株式会社
大嶋さんの論文:Analysis and design of elastic materials formed using 2D repetitive slit pattern
Daniel Piker:Kangaroo-examples
hiroaki saito:GH C#_Divide Distance With List
