2021年度第8回デジラボ：Pythonの高速化-cython f2py編-

はじめに

こんにちは、デジラボ12月担当のM2竹下佳太、M2渡辺哲平、M2齋藤魁利です。
今回も、計算速度の高速化の方法について説明します。cython、f2pyを使って高速化させます。
宜しくお願いします。

Google ColabでCythonを動かす

Google Colabとは？

Colaboratory（略称: Colab）は、ブラウザから Python を記述、実行できるサービスです。次の特長を備えています。
・環境構築が不要
・GPU への無料アクセス
・簡単に共有
Colab ノートブックは、Colab がホストする Jupyter ノートブックです。Jupyter プロジェクトの詳細については、jupyter.org をご覧ください。

おいしい数学

Google Colabの利点

• 引用にも上げた通り、Anaconda等のpython環境を作らなくてもpythonをすることができる。

• プレインストールされていないモジュールも `pip install` `conda install` できる。

• Jupyter ノートブックの利点

  • `import` が重いモジュールでも、セル１つ１つで実行することができるので、１回 `import` させればあとはリスタートさせない限りモジュールを実行させなくてもよくなるため、開発がしやすい。

  • コード内にmarkdownを入れることができるため、何をしているのかが書きやすくなる

Google Colabを触ってみる

では実際にGoogle Colabを触ってみようと思います。
以下のURLに飛んでください

Google Colaboratory

こちらは、Colaboratoryの説明です。
コードセルを実行してみましょう。
‘セルを実行‘や、セルをクリックしてctrl+enterで実行できます。

seconds_in_a_day = 24 * 60 * 60
seconds_in_a_day
---
86400

実行させると答えが返ってきます。
pythonのようにprintをさせなくても、最後の行に変数を持っていくことで表示させることができます。

さらに、実行した変数はそのノートブック内で保持され、別のセルから読み取ることもできます。

ではCythonで区分求積法をやってみましょう

Cythonで区分求積法

以下のフォルダをダウンロードし、Gdriveに入れて開くことでGoogle Colabができます。

デジラボ12月 - Google ドライブ

区分求積法の説明は前回のデジラボでやってます。

では、実際にやっていきます。まずはインポートです。

import numpy as np
import csv
import time
%load_ext Cython

ここで、JupytherでのCythonのインポートは `%load_ext Cython`で行います。

次にセルをCythonで作ります。

# %%cython
%%cython --annotate

cimport numpy as cnp
ctypedef cnp.float64_t f8_t

cpdef float delta(
        cnp.ndarray[f8_t, ndim=1] p, 
        cnp.ndarray[f8_t, ndim=1] du, 
        int num, int m, float dx):

    cdef int i, j
    cdef float sum = 0

    for i in range(num-1):
        for j in range(m):
            sum += (p[j]*du[i]**j)*dx
            
    return sum

Cythonのセルは前回のpyxファイルの中身と同じです。
このセルがCythonのセルであることを認識させるため、最初に`%%cython` と打ちます。
さらに `%%cython --annotate` を打ち込むと前回の `cython -a curve_c.pyx`と同じようにすることができます。

次はcsvファイルの読み込みです。

#y=ax^3+bx^2+cx+dのような曲線に対して，積分みたいなのをする．
name='./Coefficient_2'

f=open(name+'.csv', 'r')
reader = csv.reader(f)
p=[]#係数入れる
next(reader)
row=next(reader)[0:1]
m=int(row[0])#係数の数
next(reader),next(reader)
for row in reader:
	if row[0]=='': break
	p.append(float(row[1]))#係数を格納する
p=np.array(p,dtype=np.float64)

読み込みはnumba jitでやった時と同じです。
csvファイルの入れ方は左タブのファイルをクリックし、\csvファイルをドロップします。

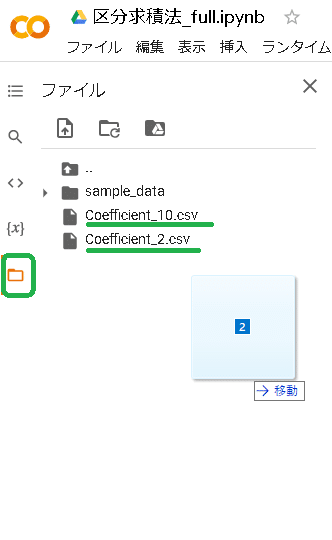
最後に実行させます。

num=1000000
du=np.linspace(0,2,num)
# t1 = time.time()
dx=du[1]-du[0]

%timeit delta(p,du,num,m,dx)

delta(p,du,num,m,dx)

`%timeit` で入力した行は、その行の実行時間を何回か回して、平均を算出することができます。

以上でGoogle ColabでCythonを動かすことができました。
前回のCythonをコンパイルする方法より、Anacondaでの環境構築やC++ビルドツールのインストールが必要ないので比較的簡単にできました。

f2py

f2pyとは

f2pyは、fortranソースをコンパイルして、pythonのモジュールを作るもの．fortranは純pythonよりも計算が早いが，コーディングが面倒くさい．
莫大な計算をfortranで解き、その結果をpythonのを利用して可視化を行うと作業の効率化ができる．

f2pyで実装

先週と同じ区分求積法の問題を解きます．

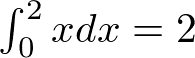
はじめに
MinGWのインストール
cmd

conda install m2w64-gcc-fortran

区分求積法を実際にfortranでかきます．
サブルーチンで関数を作ってpythonに読み込ませます．
引数は次のように書きます．

subroutine モジュール名(引数1 , 引数2 , ････ , 引数 , 返ってきてほしい数)

subroutine calc_area(p,du,num,m,dx,area)

fortranは使う変数の型をすべて指定しないといけません．
さらに，引数に配列がある際は，配列の大きさを明示しないといけません．
それぞれの型と記述方法についてまとめます．

ちなみに「!」を行頭につけるとコメントアウトしてくれます．
引数と返ってきてほしい数の指定の仕方です．
intent(in)　  引数
intent(out)　返ってきてほしい数
このように書いて引数と返ってきてほしい数を指定します．

	integer num,m,i,j
	double precision p(2)
	double precision du(1000000)
	double precision area
	double precision u
	double precision dx
	!real volume_delta
	!real delta_y
	intent(in) p,du,num,m,dx
	intent(out) area

pythonでは0から数えはじめますが，fortranでは1から数え始めるためそこに注意してコードを書き換えます．

#pythonコード	
sum=0
for i in range(num):
	u=du[i]
	for j in range(m):
		sum+=(p[j]*u**j)*dx

!fortranコード
area=0.0
do i=1 ,num
	u=du(i)
	do j=0, m-1
		area=area+((p(j+1)*(u**(j)))*dx)
	end do
end do

fortranではpythonのように算術代入演算が使えません（+=みたいなやつ）．
そのため，○=○+△のように記述します．
ちなみに，( )かっこを付ける位置を気にしないとfortranは計算ミスします．
気を付けて

以上で区分求積法の関数をfortranで書き換えられました．

subroutine calc_area(p,du,num,m,dx,area)
	integer num,m,i,j
	double precision p(2)
	double precision du(1000000)
	double precision area
	double precision u
	double precision dx
	!real volume_delta
	!real delta_y
	intent(in) p,du,num,m,dx
	intent(out) area

	area=0.0
	do i=1 ,num
		u=du(i)
		do j=0, m-1
			area=area+((p(j+1)*(u**(j)))*dx)
		end do
	end do
end

次はコンパイルです．以下のコードを実行してください．
f2py -c --fcompiler=gnu95 --compiler=mingw32 -m モジュール名 ファイル名

f2py -c --fcompiler=gnu95 --compiler=mingw32 -m calc_area calc_area.f90

コンパイル終了です．
実際に計算します．
解は2.0000が得られて，解析時間は約0.004秒でした．
高速化されています．
プログラム一式を配布します．

f2py.zip

3492 Bytes

ファイルダウンロードについて

ダウンロード

動画

今回のデジラボの様子です。

まとめ

2週にわたり，jit，cython(2種類)，f2pyの使い方，検証について紹介しました．例題として区分求積法を解きました．
得られた知見をまとめます．

純pythonに比べてとても計算が早くなったことが分かります．
f2pyが最も速い計算速度となりました．莫大な繰り返し計算を行う際にはf2pyを用いてみたらどうでしょうか．
ある程度の問題まではjitが実装が簡単で速度も比較的早いためjitをおすすめします．

これで藤田研のM2竹下佳太、M2渡辺哲平、M2齋藤魁利のデジラボを終わります．ありがとうございました．