2021年度第7回デジラボ:Pythonの高速化-numba cython編-
はじめに
こんにちは、デジラボの季節がやってきました。デジラボ12月担当のM2竹下佳太、M2渡辺哲平、M2齋藤魁利です。
今回は、pythonでいろいろしている人必見の、計算速度の高速化の方法について説明します。Numbaのjit、cython、f2pyを使って高速化させます。
宜しくお願いします。
pythonのループ計算高速化
pythonは軽量言語のひとつで比較的コーディングは簡単であるが、ループ処理が遅いという欠点があります。一方で、C言語やFORTRANは重量言語のひとつでコンパイル作業が必要ですがループ処理が早いという利点があります。ループ処理の高速化をする手法で知られるNumbaのjit、cython、f2pyを自前で用意した区分求積法のコードに適用させ、比較していきます。
jit
Numbaは、業界標準のLLVMコンパイラライブラリを使用して、実行時にPython関数を最適化された機械語に変換してます。C/C++コンパイラを別途インストールする必要はなく、比較的簡単に使えます。Anacondaだけインストールしといてください。
https://www.anaconda.com/products/individual
jitはpythonで関数(def)の上に記述して使います。
下記のようなdef文を例にjitを付け加えます。
from numba import jit
from numba import float64 as f8
from numba import int64 as i8
def keisan(a,b):
c=0
for i in range(5):
c=a+b*2
return cこのdef文はa,bという数字を引数として,cを出力します。下記の計算式が数学的に表現しました。
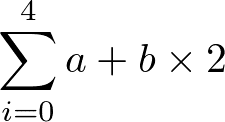
a=2.3,b=5.1の場合は,cは62.5と出力されます。
ではjitを付けていきます。
from numba import jit
from numba import float64 as f8
from numba import int64 as i8
a=2.3
b=5.1
@jit((出力の指定)(引数の指定),nopython=True)
def keisan(a,b):
c=0
for i in range(5):
c+=a+b*2
return cjitは引数と出力のint(整数)かfloat(少数)を指定する必要があります。
この場合は,aとbは少数点なので,f8と指定して,cも小数点なので,出力の方にもf8と指定します。
from numba import jit
from numba import float64 as f8
from numba import int64 as i8
a=2.3
b=5.1
@jit((f8)(f8,f8),nopython=True)
def keisan(a,b):
c=0
for i in range(5):
c+=a+b*2
return cこれで,jitを付けることができました。注意点として,nopython=Trueは指定した引数の型が間違えていた場合,pythonを実行した際にerrorを出してくれます。もし,nopython=Trueを書かなくて,引数の型を間違えたまま実行すると,上手くjitが機能せずjitが無い状態で実行してしまうので,書いた方がいいです。
以上で説明を終えます。
Cython(コンパイル)
次にCythonで高速化させます。
Cythonでは自分でsetup.pyを実行させ、コンパイルさせる方法と、
JupyterやGoogleColabを使ってする方法がありますが、
今回は自分でsetup.pyを実行する方法をします。
Cythonは公式には以下のように紹介されています。
Cython is an optimising static compiler for both the Python programming language and the extended Cython programming language (based on Pyrex). It makes writing C extensions for Python as easy as Python itself.
Cythonはあるpython演算をC/C++にコンパイルすることで、早い演算を可能にしています。
インストール
インストールは以下のコマンドのどちらかでインストールすることができます。
pip install cython
conda install cythonただし、c++のビルドツールも必要であり、Visual Studio Installerからインストールすることができます。
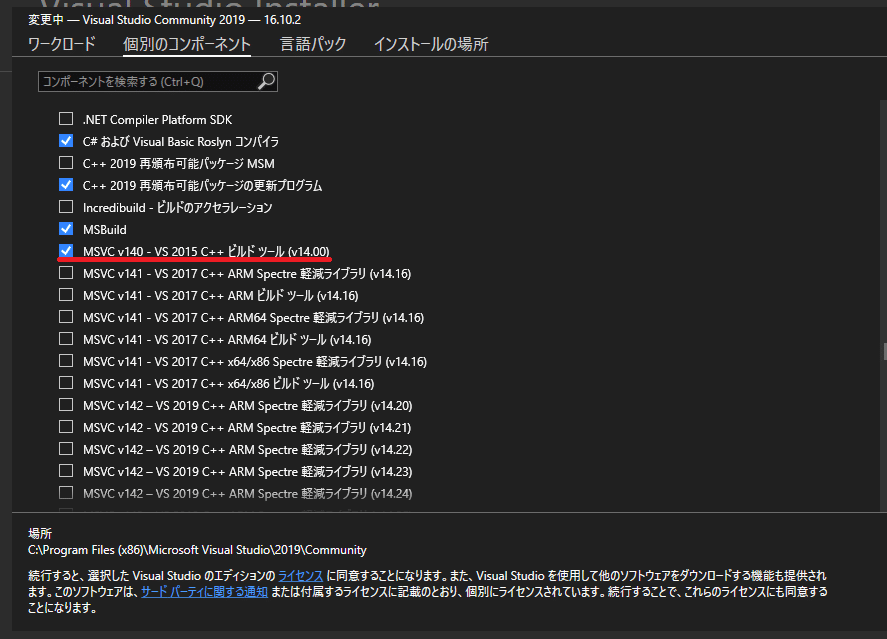
コーディング
次に先程のjitの例を使ってコーディング方法をします。
まずは、foo.pyxファイルを作ってjitの例と同じように作ります。
def keisan(a,b):
c=0
for i in range(5):
c=a+b*2
return cこれだけでも回りますが、pythonと同じ速度で回ってしまいます。
そこで、以下のように作り変えます。
cpdef float keisan(float a, float b):
cdef float c=0
for i in range(5):
c+=a+b*2
return cここで、
cpdefとはpythonのdefと同じように使えるものでpython側から読み込むことができます。
cdefはここでは変数の宣言の頭でしておりますが、コンパイルされるcの内部でしか使わないものをしています。
そして、変数の宣言では頭にfloaやint等、型を宣言することでより高速化させることができます。
次にコンパイルをさせます。
まずは、コンパイルをするsetup.pyを作ります。
from setuptools import setup
from Cython.Build import cythonize
setup(
ext_modules = cythonize("foo.pyx")
)今回はCython Hello Worldを参考にしました。
これを作成したら、以下のコマンドをそれらファイルが入っているディレクトリからコマンドプロント等で実行させます。
python setup.py build_ext --inplaceこれでコードが生成されると思います。
ライブラリ build\temp.win-amd64-3.7\Relea~~ とオブジェクト build\temp.win-amd64-3.7\Release\~~ を作
成中
コード生成しています。
コード生成が終了しました。コードが生成され、pydファイルができれば完了です。
試しにpythonから実行させてみましょう。実行の方法はpythonからインポートさせればOKです。
from foo import keisan
print(keisan(2.3, 5.1))これで62.5が表示されれば実行できました!
区分求積法で試してみる
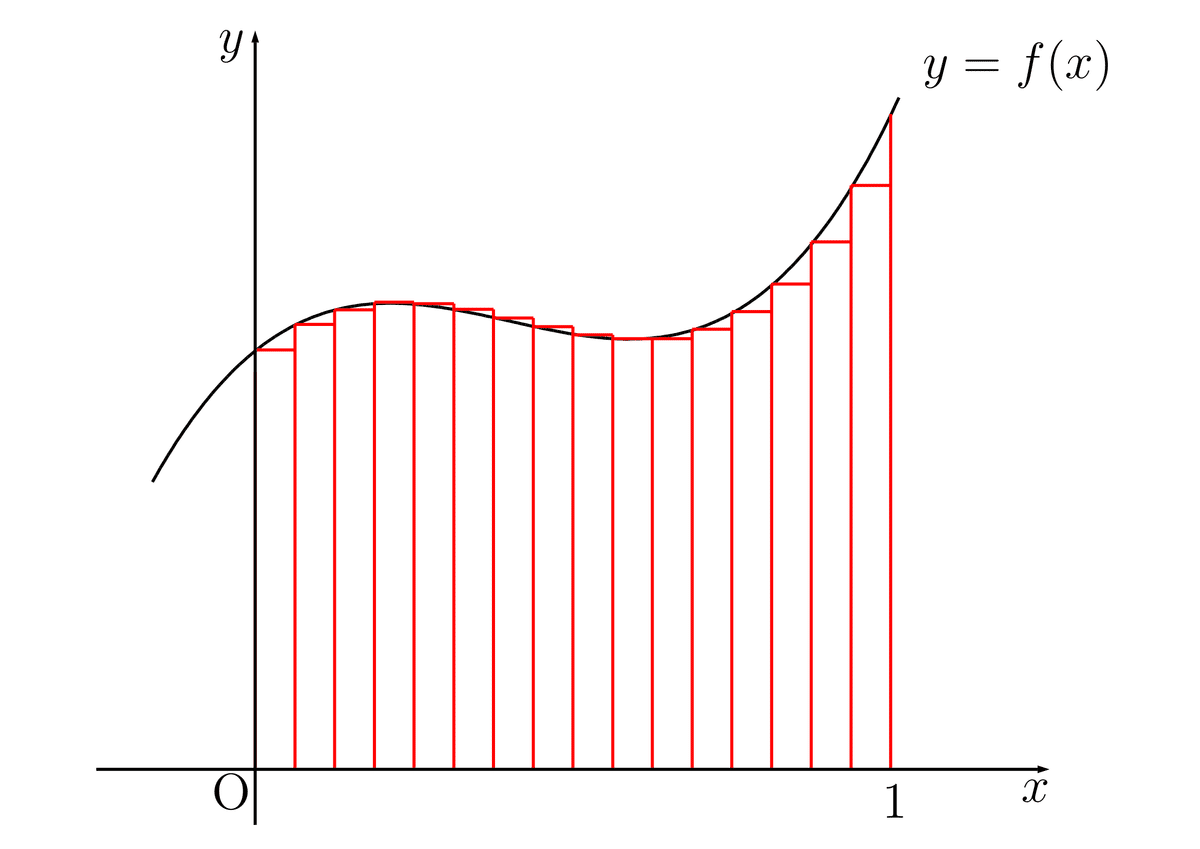
細かく分割した長方形の面積を足し合わせたもの。
今回は、分割数を大きくしてpython、jit、cythonで計算時間を比較します。
jit
今回使用するファイルです。
はじめに定積分する関数の次数と係数の組み合わせをcsvファイルに出力します。そのコードを下記に示します。
import numpy as np
import random,csv
x=[]
dimension=10 #積分する関数の次数を決める
for i in range(dimension):
addx=random.random()*5 #ランダムに係数を決める。
x.append(addx)
f=open('Coefficient_'+str(len(x))+'.csv','w',newline='') #係数と次数の組み合わせを出力
writer=csv.writer(f)
writer.writerow(['m'])
writer.writerow([len(x)])
writer.writerow(['','','',''])
writer.writerow(['Degree','Coefficient'])
for i in range(len(x)):
writer.writerow([str(i),x[i]])下記のコードで実際に区分求積法をします。
import numpy as np
import csv
from numba import jit
from numba import njit
from numba import float64 as f8
from numba import int64 as i8
import time
#y=ax^3+bx^2+cx+dのような曲線に対して,積分みたいなのをする.
name='Coefficient_2'
f=open(name+'.csv', 'r')
reader = csv.reader(f)
p=[]#係数入れる
next(reader)
row=next(reader)[0:1]
m=int(row[0])#係数の数
next(reader),next(reader)
for row in reader:
if row[0]=='': break
p.append(float(row[1]))#係数を格納する
p=np.array(p,dtype=np.float64)
num=1000000 #分割数を決定
du=np.linspace(0,2,num)
#p=p.tolist()
#du=du.tolist()
t1 = time.time()
dx=du[1]-du[0]
@jit((f8)(f8[:],f8[:],i8,i8,f8),nopython=True) #jitを適用
def delta(p,du,num,m,dx):
sum=0
for i in range(num):
u=du[i]
for j in range(m):
sum+=(p[j]*u**j)*dx
return sum
sum=delta(p,du,num,m,dx)
t2 = time.time()
f=open('Analysis time'+'.csv','w',newline='')
writer=csv.writer(f)
writer.writerow(['Analysis time'])
writer.writerow([t2-t1])
print(t2-t1)
print(sum)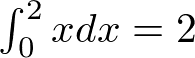
例題2を分割数1000000として区分求積法で解きます。
引数の説明をします。
pが係数を格納しているベクトル。この場合はy=xを積分したいので,p=[0,1]となります。
duは0から2の範囲を1000000個に分割したパラメーターのベクトル,分割が大きいと,sumの値が2に近づきます。
numがパラメーターの分割数。
mが係数の個数。
dxが図:区分求積法のイメージに示している赤色の長方形の幅を示しています。なので,numが大きいとdxの値は小さくなります。
また,引数がベクトルの場合は,f8[:]としないといけません。
マトリックスの場合はf8[:,:]となります。
解析時間は約0.005秒でした。
Cython
今回使用するファイルです。
定積分する関数の次数と係数の組み合わせをcsvファイルに出力するコードはjitと同じになります。
コンパイルさせるcurve_c.pyxを記述します。
cimport numpy as cnp
ctypedef cnp.float64_t f8_t
cpdef float delta(
cnp.ndarray[f8_t, ndim=1] p,
np.ndarray[f8_t, ndim=1] du,
int num, int m, float dx):
cdef int i, j
cdef float sum = 0
for i in range(num-1):
for j in range(m):
sum += (p[j]*du[i]**j)*dx
return sumここではnumpyの配列(np.array)を読み込むため、工夫をしています。
cimportでnumpyをインポートしています。
ctypedefでnumpyで言うfloat64をf8_tとして宣言。
変数p, duはnp.arrayであるため、cnp.ndarray[f8_t, ndim=1]で宣言してます。[型, ndim = 次数]のような感じです。
次にsetup.pyをつくります。
from distutils.core import setup, Extension
from Cython.Build import cythonize
from numpy import get_include
ext = Extension(
"curve_c",
sources = ["curve_c.pyx"],
include_dirs = ['.', get_include()]
)
setup(name = "curve_c", ext_modules = cythonize([ext]))ここでもnumpyを使うために、get_include()を使っています。
次に、コードの中で重そうな処理を探します。
以下のコマンドをコマンドプロントで実行させてみましょう。
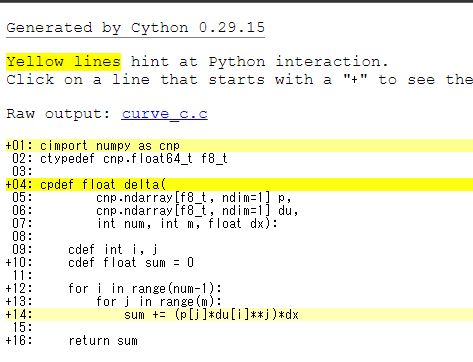
cython -a curve_c.pyxするとcurve_c.htmlファイルが作られるとおもいます。
黄色で示される部分がC/C++で行数がかかっている部分です。
できるだけ黄色の部分がないように作ります。
curve_cython.pyでコンパイルと計算を両方させます。
コンパイルはsubprocessでコマンド入力させます。
import numpy as np
import csv, time, subprocess
subprocess.check_call([
'python',
'setup.py',
'build_ext',
'--inplace'])
from curve_c import delta
#y=ax^3+bx^2+cx+dのような曲線に対して,積分みたいなのをする.
name = 'Coefficient_2'
f = open(name + '.csv', 'r')
reader = csv.reader(f)
p = []#係数入れる
next(reader)
row = next(reader)[0:1]
m = int(row[0])#係数の数
next(reader), next(reader)
for row in reader:
if row[0] == '': break
p.append(float(row[1]))#係数を格納する
p = np.array(p, dtype = np.float64)
num = 1000000
du = np.linspace(0, 2, num)
t1 = time.time()
dx = du[1] - du[0]
sum = delta(p, du, num, m,dx)
t2 = time.time()
f = open('Analysis time' + '.csv', 'w', newline = '')
writer = csv.writer(f)
writer.writerow(['Analysis time'])
writer.writerow([t2 - t1])
print(t2 - t1)
print(sum)subprocess.check_call関数を使うことで、エラーが起こった場合にエラーを返して処理を止めるようにしてます。それとモジュールインポート以外は、jitでコーディングしたものと同じものになります。
あとはjitと同じ条件で区分求積法を解きます。
解析時間は約0.012秒でした。
動画
今回のデジラボの様子はこのようになってます。
まとめ
今回のデジラボでは、jit,cythonの実装の仕方を説明し、例題を解きました。解析時間と手法についてまとめたものを示します。
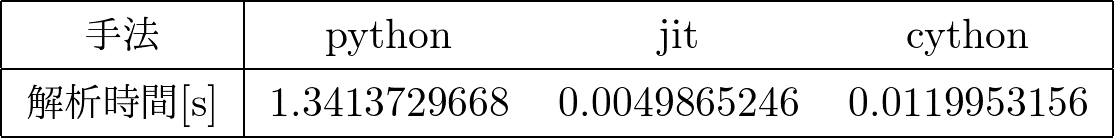
解析時間としては、純粋なpythonと比べてjitは約270倍、cythonは約112倍ほど速くなりました。jitはcythonと比べて実装が簡単なため、jitおすすめします。
次回は、GoogleColabでcythonとf2pyの実装を行い、今回と同じ例題を解いて比較します。
ありがとうございました。
