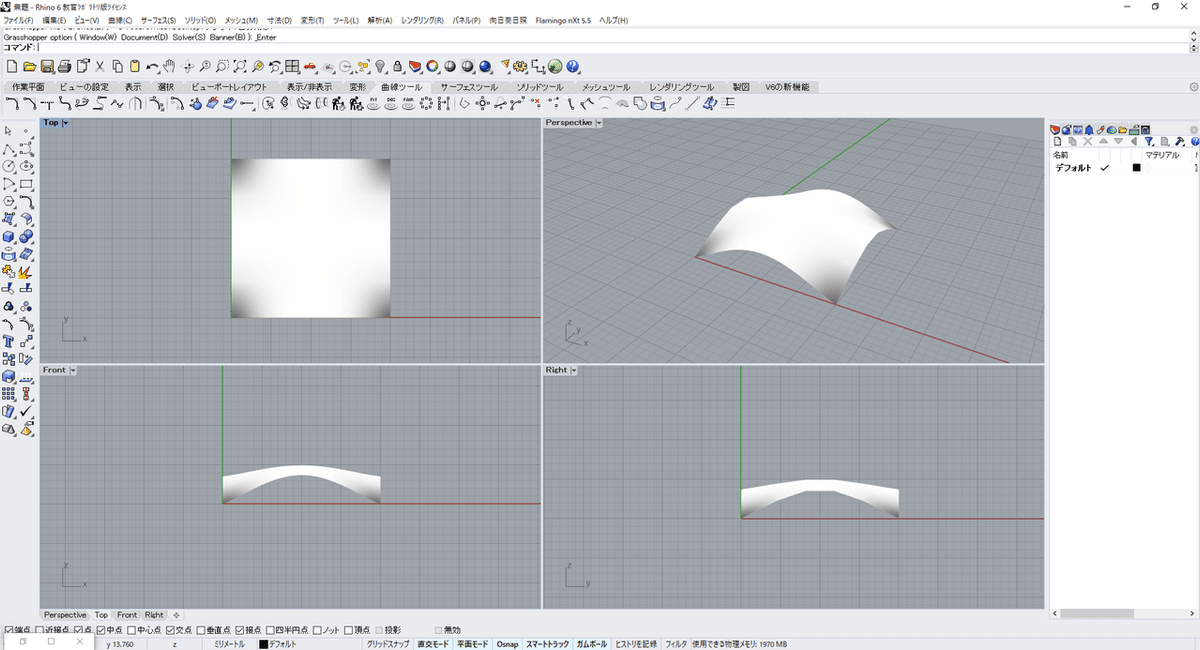
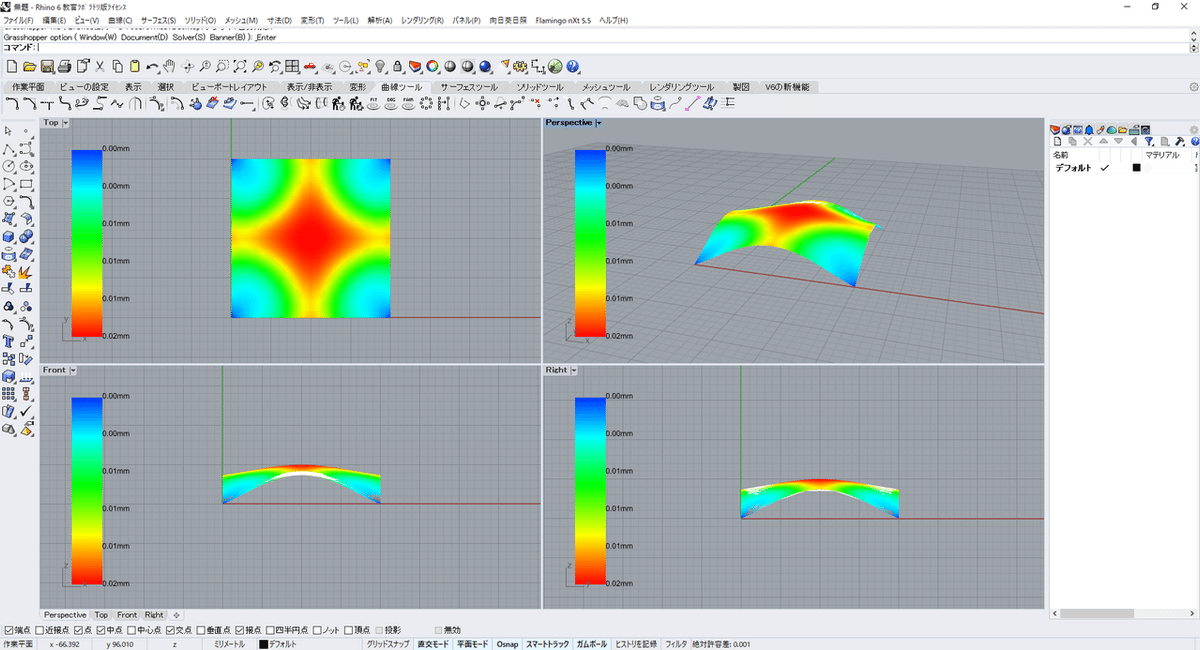
2020年度第9回デジラボ：OpenSees for Grasshopperでシェルの板厚分布を考慮した形態創生をしてみる

はじめに

北九大藤田研M1渡辺哲平です。今回はOpenSees for Grasshopperを用いて，シェルの形態創生をします。藤田先生が過去にアップロードしていただいているものを派生させています。これを機にいろいろな形態創生手法をGrasshopperを用いて視覚的に試せたらいいなと思っています。

OpenSees for Grasshopperのインストール

過去に紹介しているため割愛します。

実際に形態創生してみます

とりあえず，シェルの形状最適化の復習から

シェルの形状最適化は，目的関数ｰひずみエネルギー，設計変数ｰBスプライン関数により離散化をして解くことが一般的になっています。

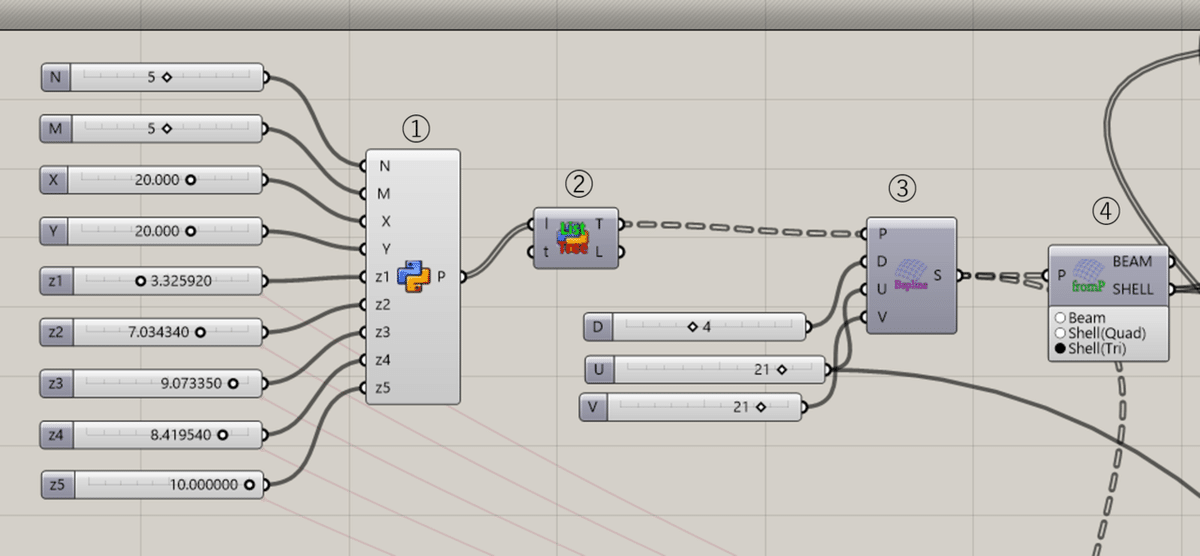
①制御点座標情報の入力

Bスプライン関数

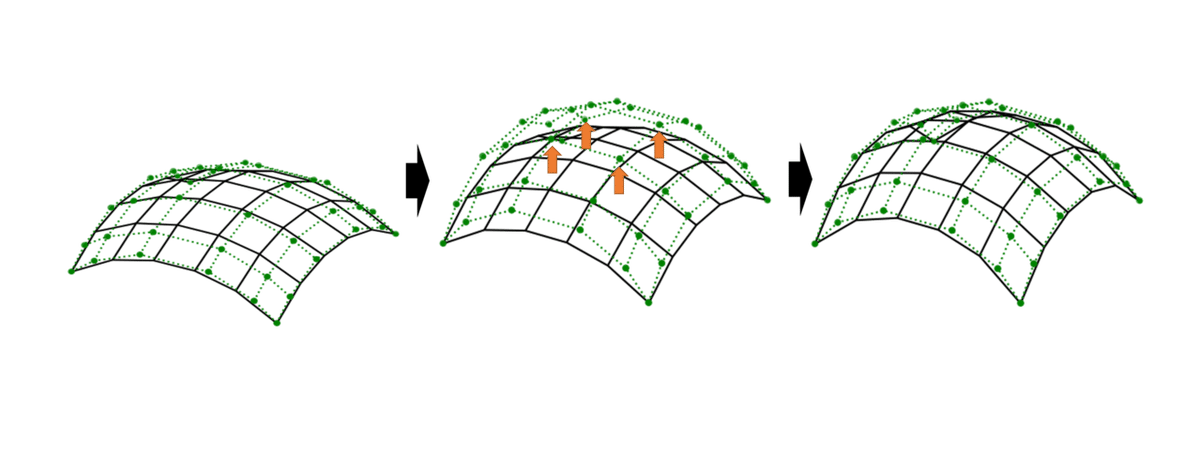
制御点，B-スプライン基底関数，およびノットベクトルによって定義されるパラメータ表示された曲面

制御点座標が変化すると，それに伴って節点座標が変化する。制御点によって形状を変化させるため，多くの節点座標を直接動かすより圧倒的に変数が小さくなります。

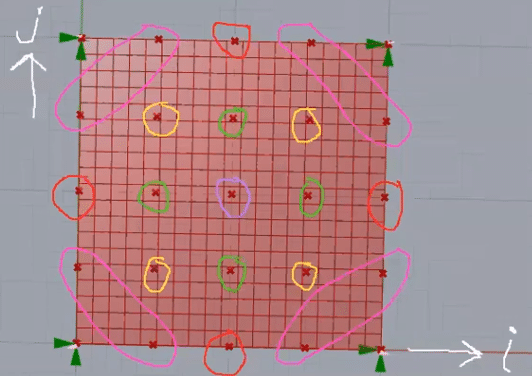
①では，GHpythonを用いてBスプライン関数の制御点座標の情報を与えています。シェル構造物は力学的性状に対称性を有しているため，対称性を考慮して制御点を反転させていく。

分かりやすくするためにz1~z5はとりあえず0でいれてみてください。

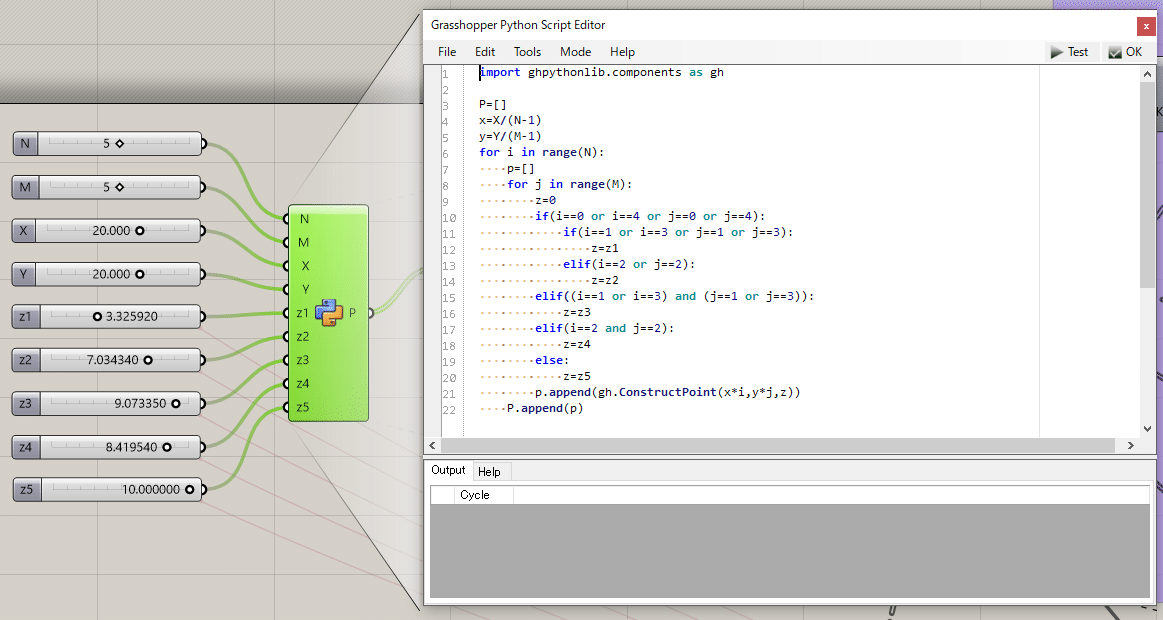
import ghpythonlib.components as gh

P=[]
x=X/(N-1)#x方向の制御点スパン
y=Y/(M-1)#y方向の制御点スパン
for i in range(N):
   p=[]
   for j in range(M):
       z=0
       if(i==0 or i==4 or j==0 or j==4)
           if(i==1 or i==3 or j==1 or j==3):#ピンクの対称性を考慮して反転させる
               z=z1
           elif(i==2 or j==2):#オレンジの対称性を考慮して反転させる
               z=z2
       elif((i==1 or i==3) and (j==1 or j==3)):#黄色の対称性を考慮して反転させる
           z=z3
       elif(i==2 and j==2):#紫の点を反転させる
           z=z4
       else:
           z=z5#緑の対称性を考慮して反転させる
       p.append(gh.ConstructPoint(x*i,y*j,z))#得られた制御点座標を集合Pに格納
   P.append(p)
 #今回の支持点(隅部4点)は変数としない。

1,このpythonコードをGHpythonに入力

②，Sets > List > Convert list and tree　でGHpythonのリストとツリーをコンバートする。

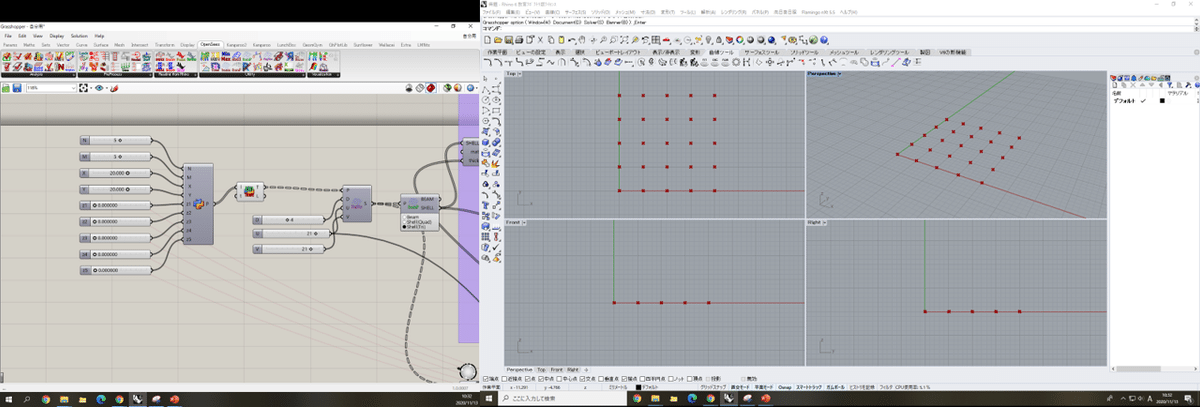
③シェルの節点座標を取得

OpenSees > Utility > Rational B-spline Surface (RBS)　　に，スプライン関数の次数(D)(今回は制御点の数-1とする)，U,V方向の節点数(Ｕ,V)を入力

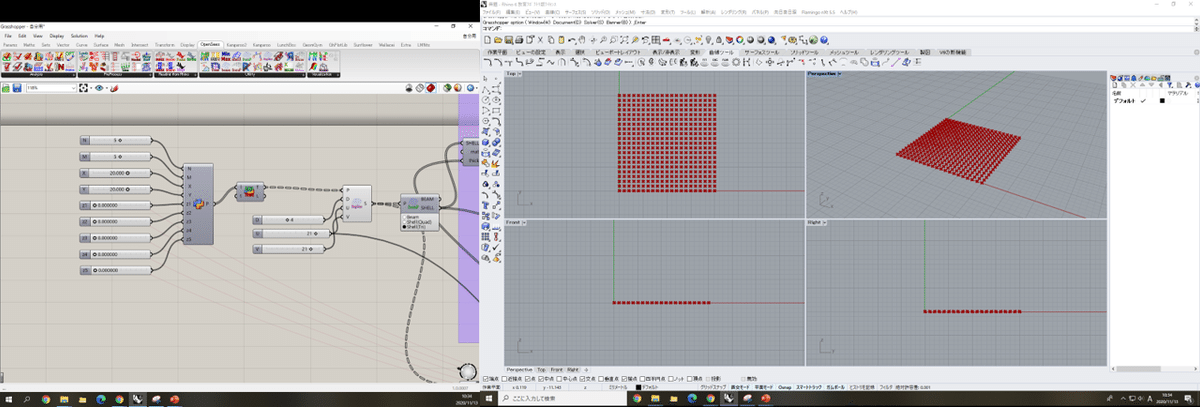
④シェルの生成

OpenSees > Utility > FromGridPoints　　をshell(Tri)に✅をつける。

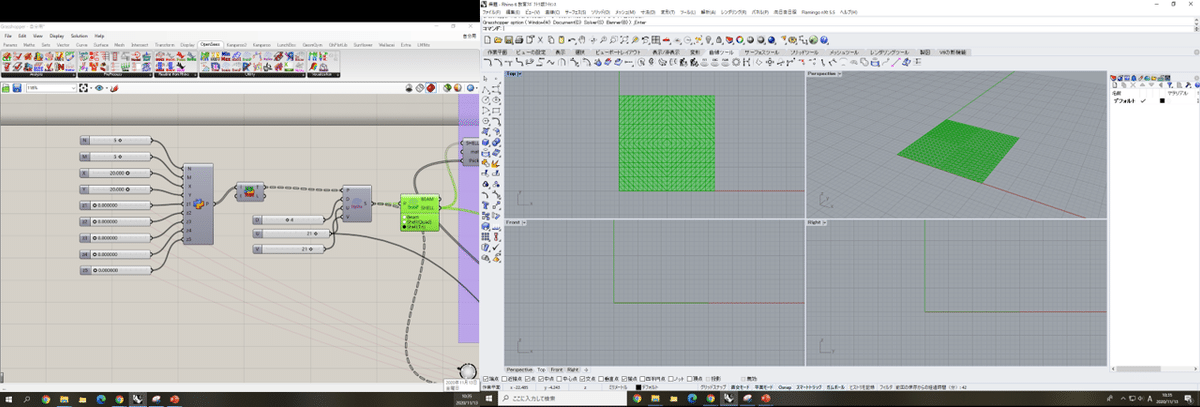
これでシェルは作れたと思います。

境界条件，荷重の与え方は下記URLを参照してください。thicknessに入れる値は下で説明します。

https://www.youtube.com/watch?v=xTSRX_ZjiEg

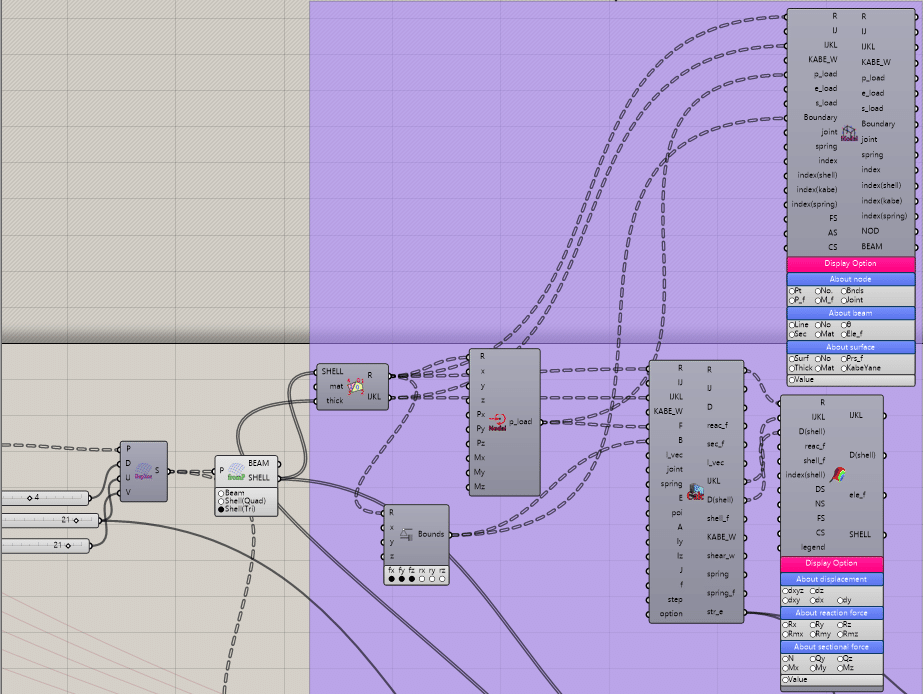
やっと板厚分布最適化にすすみます

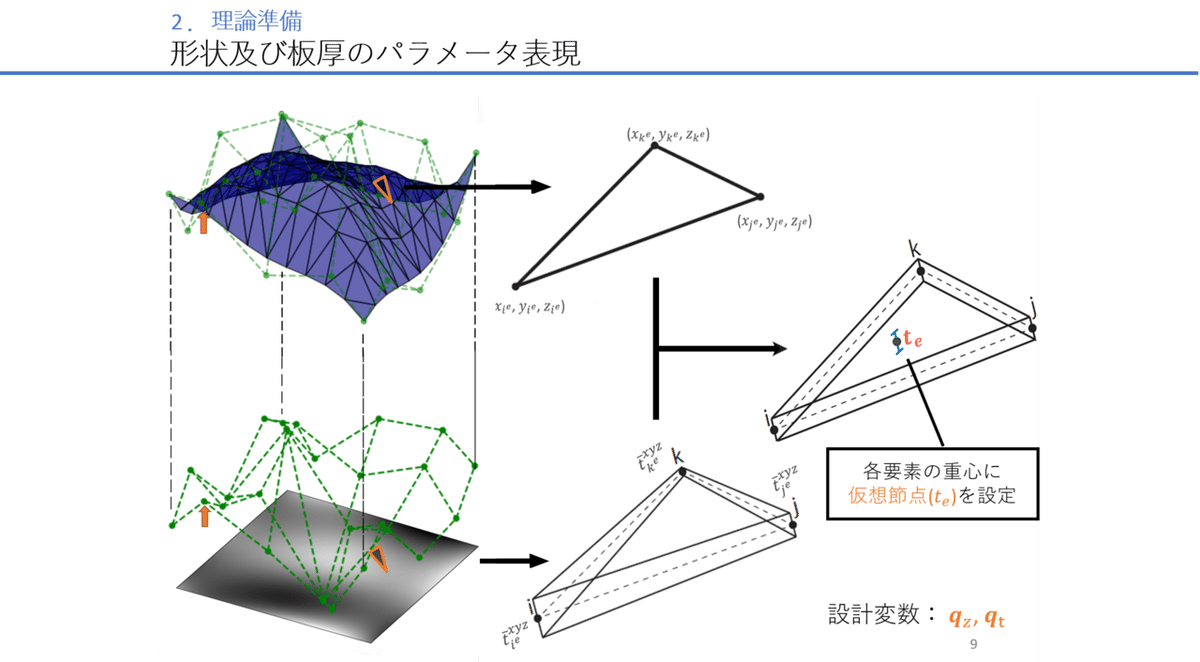
変数を減らすため形状をスプライン関数で離散化したのと同様に，板厚もスプライン関数で離散化します。板厚も各要素で与えられている情報なのでスプライン関数で離散化することで変数を減らすことができます。

有限要素解析は要素内一定の板厚として定義されているため，各要素の重心に節点位置がくるよう新たなスプライン関数を定義してそのz座標を要素板厚とします。

まず，形状のとき使ったGhpythonコードを流用しようとする

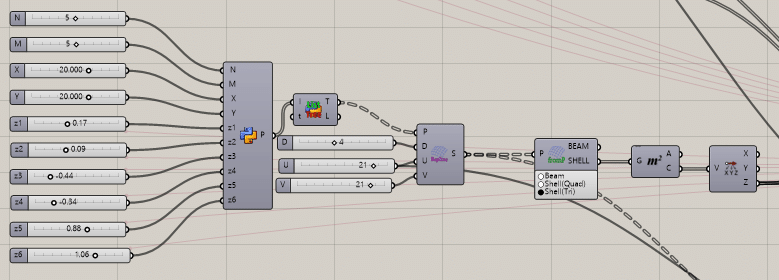
そのままコピペしてください。

若干変えるところがあります。板厚分布最適化は，支持点における板厚も変化したほうが良いので，支持点の対称性を考慮して変数としていきます。

Number Sliderの名前をz6として一つ追加してください。

import ghpythonlib.components as gh

P=[]
x=X/(N-1)#x方向の制御点スパン
y=Y/(M-1)#y方向の制御点スパン
for i in range(N):
   p=[]
   for j in range(M):
       z=0
       ###########追加###########
       if((i==0 or i==4) and (j==0 or j==4)):#支持点の対称性を考慮
           z=z6
       ##########################
       if(i==0 or i==4 or j==0 or j==4)
           if(i==1 or i==3 or j==1 or j==3):#ピンクの対称性を考慮して反転させる
               z=z1
           elif(i==2 or j==2):#オレンジの対称性を考慮して反転させる
               z=z2
       elif((i==1 or i==3) and (j==1 or j==3)):#黄色の対称性を考慮して反転させる
           z=z3
       elif(i==2 and j==2):#紫の点を反転させる
           z=z4
       else:
           z=z5#緑の対称性を考慮して反転させる
       p.append(gh.ConstructPoint(x*i,y*j,z))#得られた制御点座標を集合Pに格納
   P.append(p)
 #今回の支持点(隅部4点)は変数としない。

これで制御点座標を定義することができました。

先程いったように，各要素の重心に節点位置がくるよう新たなスプライン関数を定義してそのz座標を要素板厚とします。

surface > Analysis > Area　　を　　

OpenSees > Utility > FromGridPoints　　につなげる。得られた各要素の重心のz座標が欲しいので，

Vector > Vector > Deconstruct Vector(DeVec)　　をつなげて，z座標をthicknessとします。

以上で板厚の定義は終了！！！

最適化計算をする

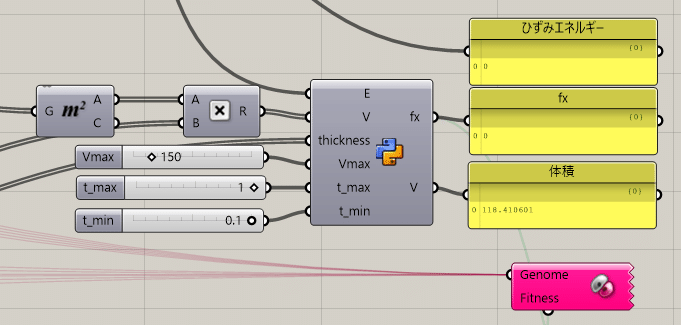
GHpythonの中身

V=sum(V)#各要素の体積を合計する。
fx=E+(max(Vmax,V)-Vmax)*100+(max(t_max,max(thickness))-t_max)*100
+(t_min-min(t_min,min(thickness)))*100
#ひずみエネルギー+体積の上限値+板厚の上限値+板厚の最小値

形状におけるOpenSees > Utility > FromGridPoints　---→　surface > Analysis > Area　　　で各要素の面積を求める。

math > Operators > Multiplication　　　をつかって，各要素の面積×板厚をして各要素の体積を求める。

pythonコード内で制約をペナルティ項として入力する。

例えば，　(max(Vmax,V)-Vmax)*100　　((体積の上限値と現在の体積を比較して大きい方)-体積の上限値)×100(スケール)

このペナルティ項を入れることで体積が上限値を超えたとき，目的関数にペナルティがかかる。

Params > Util > Galapagos　　に目的関数 fx と設計変数 z1~z5，z1~z6をつなげる。

Galapagosを実行したら形状と板厚分布の同時最適化が実行される！

終了！

結果を下に示します。noteで説明が不十分なところはYoutubeに載せてますので是非。https://www.youtube.com/watch?v=oE3SQm34MJk

Youtubeでは最適化結果の可視化まで行っています！

ガラパゴス結果

支持点近傍の板厚が大きくなってライズがカテナリー状に上がる