2022年度第1回デジラボ（前半）：斜め柱を考慮した柱配置最適化

fujitalab

配布データ

動画で使用したデータの配布と、確認用の最終データの配布です。
＊配布データの組み立てを説明予定ですので、１から作り上げたい方は、配布データをスキップしてお読みください。また、配布データを使用する方で、配布データまでの説明が不要な方はタイトル最初に★がついている「★構造解析：長期荷重と短期荷重」までスキップしてお読みください。

・動画の開始時データと一緒の配布用データ

・解析化開始前、確認用の最終データ


投稿動画


はじめに

こんにちは。2022年度第1回デジラボを担当するM2門司,M1新田,舟津,B4安部です。前半のテーマは「Wallaceiを使ってひずみエネルギーを最小化する斜め柱を考慮した柱配置最適化をしてみよう。」です。Grasshopper（以下Gh）のWallaceiという最適化のコンポーネントを利用して、柱の座標を設計変数、ひずみエネルギーを目的関数とする最適化手法の紹介です。動画と一緒に進めていくことをお勧めします。 
　お詫び：動画内では、時間短縮のために、モデル作成、柱梁種類、境界条件、面荷重等のコンポーネントを予め作成・組み立てしたデータを使用し説明しています。ご了承ください。
　コンポーネントについての詳しい説明はこちらのwikiページを参照ください。

タイトル画像


事前にインストールする必要があるもの

最適化コンポーネント Wallacei をインストールします。
詳しいインストール方法は2020年度第4回デジラボにて紹介しています。


-------------------説明内容--------------------

目次

・目的
　今回最適化する目的です。
・モデル説明(初期条件)
　動画内の事前に配布しているデータの説明です。ここではモデル作成からお話しします。
・荷重説明
　解析をする上で必要となる自重と長短期荷重についての説明です。
・★構造解析：長期荷重と短期荷重
　長期荷重（自重）と短期荷重（地震）による構造解析を行います。
・最適化説明
　制約のかけ方についての説明です。 今回は、20m×20mという広い空間のなかで、柱頭座標が正方形平面中心より12m×12m空間上座標に柱頭の座標が配置されない最適化を行います。また、制約条件のかけ方について説明します。
・CSV出力説明
　最適化で扱ったデータをCSV出力するための説明です。


目的

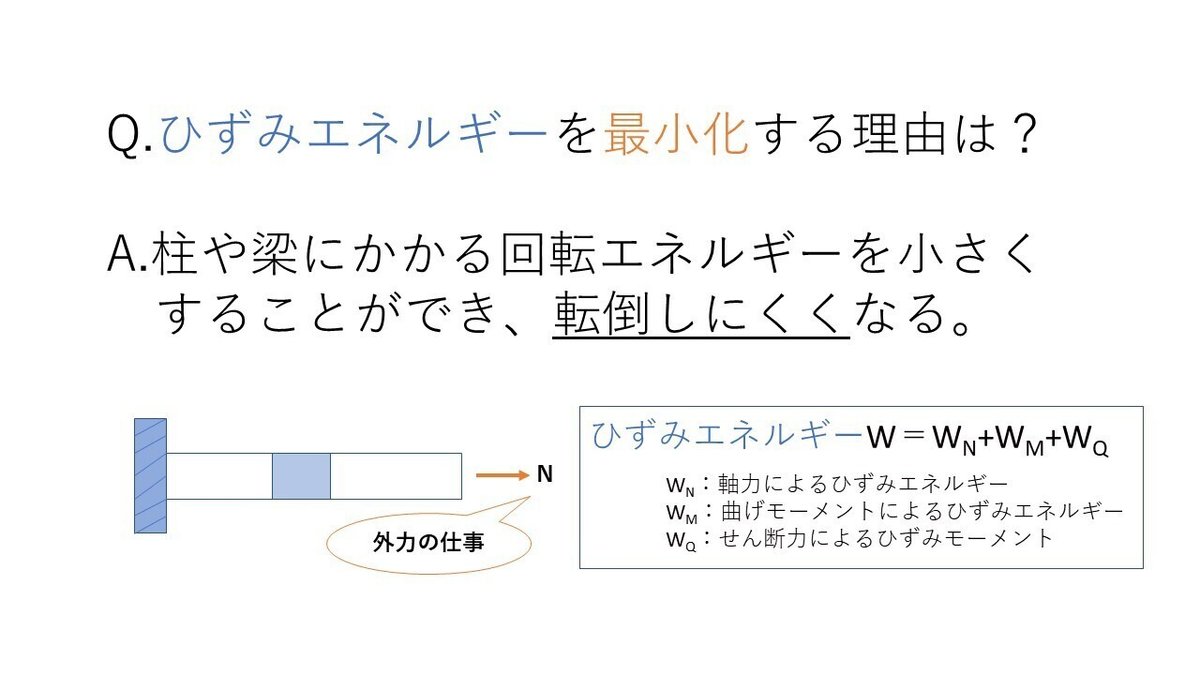
　今回の最適化は鉛直柱または斜め柱のどちらかを選択しながらひずみエネルギーを最小化し、柱配置を最適化します。ひずみエネルギーを小さくすることで柱や梁にかかる回転エネルギーを小さくすることができ、転倒しにくくなります。
　＊注意点：斜め柱が選択されることで回転エネルギーを小さくできますが、デメリットとしてひずみが考慮されていないことに注意してください。

ひずみエネルギー最小化の理由


モデル説明（初期位置の説明）

　Grasshopperを新しく起動したところから柱梁のモデルを作成していきます。前提条件・GHPythonによるモデル作成・柱梁情報の計算, 格納等・境界条件の順で説明します。

■モデルの前提条件（内容）
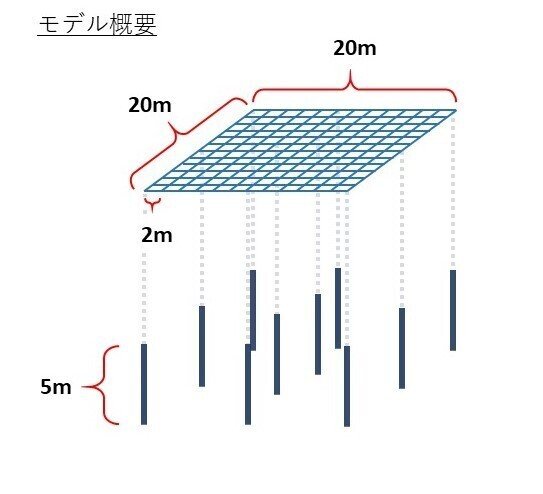
・最適化範囲： XY方向20m×20mグリッド（正方形平面）
・柱最適化位置：各XY方向10分割、つまりスパン2mでの配置
・階高：5m(制約をかける仕様上、階高3mだとひずみエネルギーを最小化するための斜め柱が選択されないため注意が必要です。)
・柱の本数：10本（動画作成時の解析時間短縮のため10本にしています。）

モデル説明

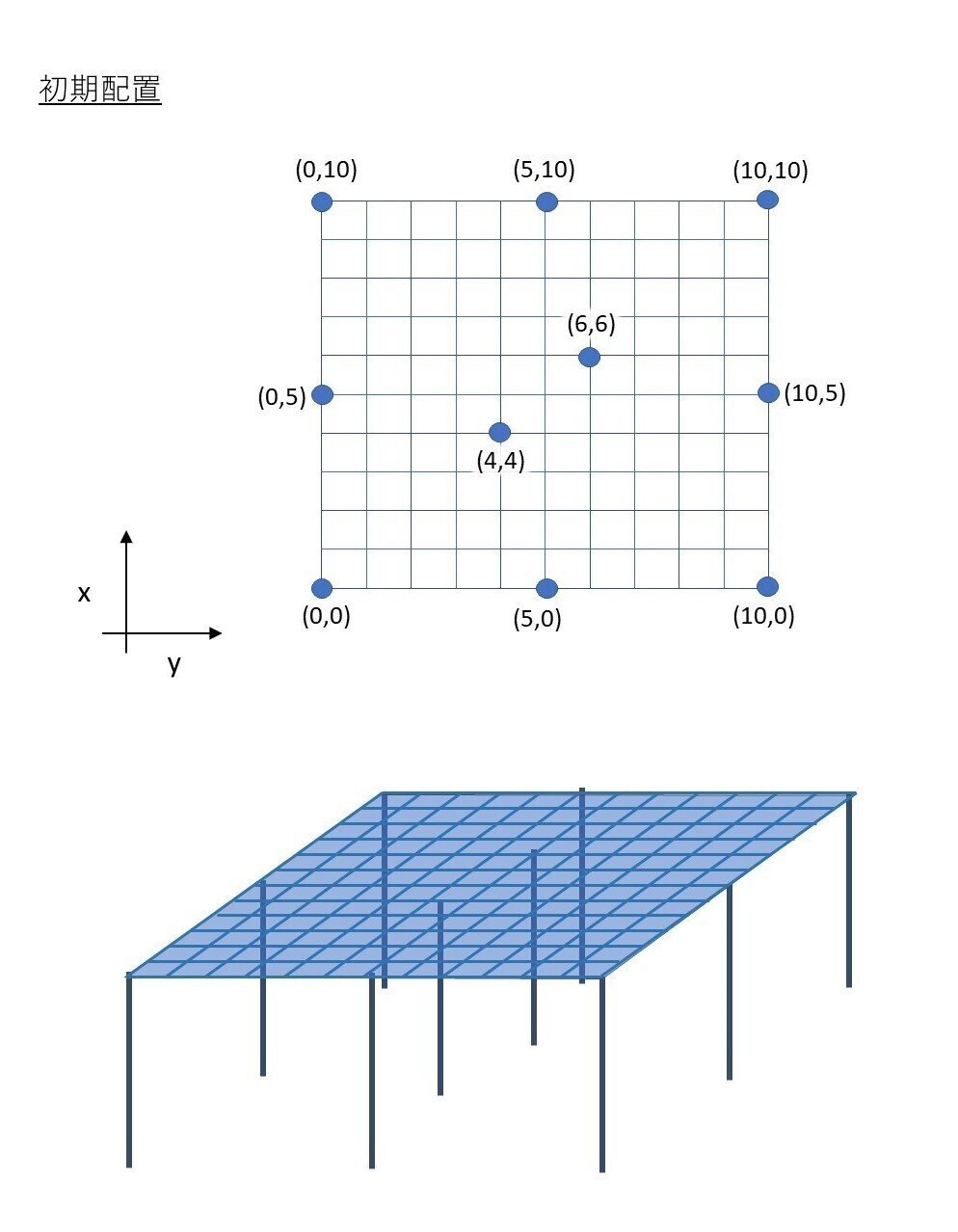
柱初期配置

制約条件2


　モデル作成は基本的にGHPythonで作成していきます。正方形平面はPythonのプログラム内で作成できますが、柱を構成するために柱頭と柱脚の座標が必要になるプログラムを組み立ています。動画の順と同様、Python内説明後に、柱頭と柱脚の座標決定について説明します。

■Pythonによるモデル作成（モデル作成GHPythonコンポーネント）
（ N : x方向 接点数, M : y方向 接点数, X : x方向 梁の長さ, Y : y方向 梁の長さ, ｌ: 階高, ｘ : 柱頭x座標, ｙ : 柱頭y座標, xl : 柱脚x座標, yl : 柱脚y座標） 　Maths<Script<GHPythonからGHPythonを取り出します。すると下記画像内左のようになっています。こちらの状態から右になるように説明をしていきます。名前変更は変更したい要素のポインター位置で右クリック、最上部が名前変更場所です。GHPython左側・右側の名前は、コード内の名前や接続コンポーネントと連動している場合があるため注意してください。

画像6

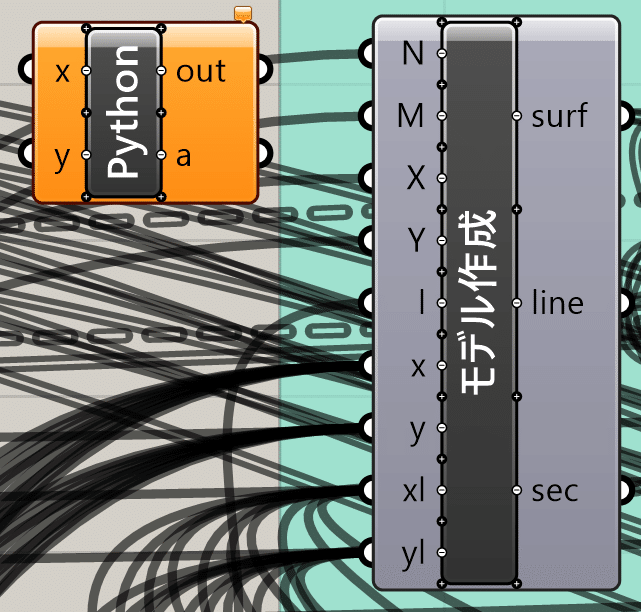
　左側に９つ枠が入るように＋ボタンを押して増やします。上から順に、N, M, X, Y, l, ｘ, ｙ, xl, ylです。

画像7

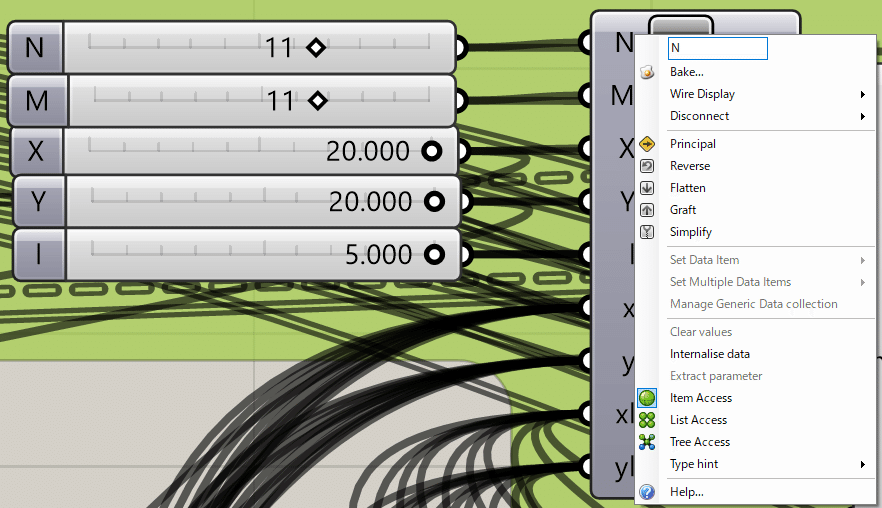
　N, M, X, Y, lに値を自由に変化できるスライダーを付けます。今回は、 N, M, X, Y, lそれぞれに11, 11, 20, 20, 5の値を使用しつなぎます。スライダーの作り方の例は、GH上でダブルクリック＜「0.0<20.0<20.0」と記入することで範囲0.0~20.0（20.0選択）のスライダーを作ることができます。（上記画像参照）
　右側に３つの枠が入るようにしますが、基本的にoutは使用しないので－ボタンで消してください。（以降のGHPythonで、outを使用しません。）上から順に、surf（面情報）, line（梁情報）, sec（セクション番号）です。ここでエラーになる場合は、＋ボタンで要素を一つ増やして－ボタンで出した要素を消すことで解決することがあります。

　次にPythonのコード中身についてです。コードは以下のように書いてください。＃の後は簡潔な説明を書いており、プログラムに影響はありません。 

import ghpythonlib.components as gh

pitchx=X/(N-1)
pitchy=Y/(M-1)

line,surf,sec=[],[],[]

for i in range(len(x)):
       xi=x[i]*pitchx
       yi=y[i]*pitchy
       xi2=xl[i]*pitchx
       yi2=yl[i]*pitchy
       r1=gh.ConstructPoint(xi,yi,0)#柱頭
       r2=gh.ConstructPoint(xi2,yi2,-l)#柱脚
       line.append(gh.Line(r1,r2))
       sec.append(1)

for i in range(N):
   for j in range(M-1):
       xi=j*pitchx
       yi=i*pitchy
       xj=(j+1)*pitchx
       yj=i*pitchy
       r1=gh.ConstructPoint(xi,yi,0)#i端
       r2=gh.ConstructPoint(xj,yj,0)#j端
       line.append(gh.Line(r1,r2))
       sec.append(0)
       if(i!=N-1):
           xk=xj
           yk=(i+1)*pitchy
           xl=xi
           yl=yk
           r3=gh.ConstructPoint(xk,yk,0)#i端
           r4=gh.ConstructPoint(xl,yl,0)#j端
           surf.append(gh.x4PointSurface(r1,r2,r3,r4))

for i in range(M-1):
   for j in range(N):
       xi=j*pitchx
       yi=i*pitchy
       xj=j*pitchx
       yj=(i+1)*pitchy
       r1=gh.ConstructPoint(xi,yi,0)#i端
       r2=gh.ConstructPoint(xj,yj,0)#j端
       line.append(gh.Line(r1,r2))
       sec.append(0)

■柱頭座標決定 
　柱頭座標は、モデル作成コンポーネント(GHPython)のx, yにつなげるために、スライダーで作成していきます。
　スライダーは、接点数が11個つまり、座標が0-10の11つの範囲であることに注意してください。下記画像のようにスライダーを作りましょう。ｘ方向ｙ方向の2方向にあるため、スライダーの数は合計２０個あります。同じものをコピー＆ペーストすることで素早く作ることができます。スライダーの名前をx1, y1, x2, y2のように変更することも忘れないで下さい。

画像44

画像46

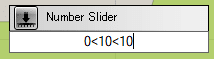
■柱脚座標決定
　柱脚座標は、モデル作成コンポーネントのxl, ylにつなげるために、スライダーで作成していきます。柱頭座標のそれぞれｘｙ座標に±１または0を足すという制約をかけ斜め柱を考慮するスライダーを作っていきます。全体として下記画像のようになっています。

画像45


　まず左の説明です。スライダーは、「-1＜0＜1」であることに注意してください。下記画像のようにスライダーを作りましょう。x方向y方向の2方向にあるため、柱頭座標同様、スライダーの数は合計２０個あります。同じものをコピー＆ペーストすることで素早く作ることができます。スライダーの名前を偏差を表すdx1, dy1, dx2, dy2のように変更することも忘れないで下さい。

画像9

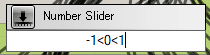
　次に右の説明です。柱頭座標と偏差を足すPythonを組むことで柱脚座標を決定します。
　まずGHPythonを取り出します。下記画像になるように説明をしていきます。コンポーネントの左右の数・名前を下記画像を参考に変更してください。左は変数のため、適宜変更ください。

画像10

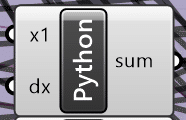
　GHPythonのコード中身は下記のようになっています。下記コードを参考にx1-10, y1-10のGHPythonを作成して下さい。x1の「1」は、小文字のLではなく、柱頭座標を表す数字であることに注意してください。 

sum=x1+dx

　モデル作成へつなぐ前のGHPythonコンポーネントをコピー＆ペースト、編集することで時短しましょう。
　コンポーネントのつなぎ方は下記画像のようになっています。下記画像を参考にx1-10, y1-10のGHPythonにつなげて下さい。柱頭座標を表すx1をGHPythonコンポーネントのx1に、偏差を表すdx1を GHPythonコンポーネントのｄxにつなぎます。

画像11

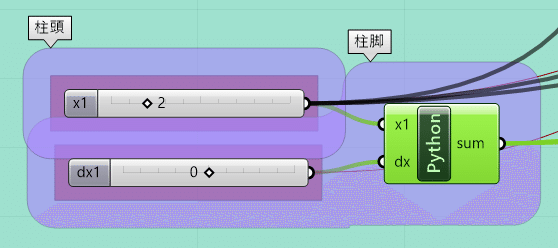
　以下同様にして柱脚座標となるGHPythonをx方向y方向それぞれ計２０個作成します。

■モデル作成GHPythonコンポーネントへのつなぎ方
（ x : 柱頭X座標, y : 柱頭Y座標, xl : 柱脚X座標, yl : 柱脚Y座標 ）
　モデル作成GHPythonコンポーネントへのつなぎ方は、下記画像を参考に、x, y, xl, ylにつなぎます。１から１０すべてつなぐことに注意してください。

画像12

画像13

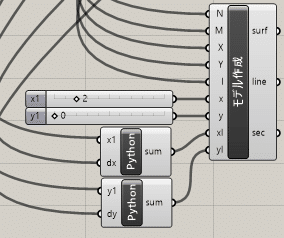
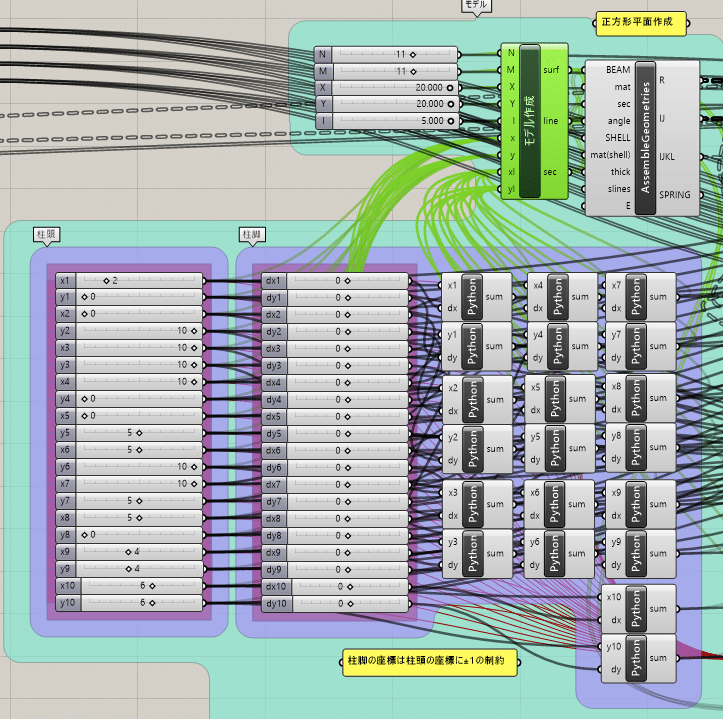
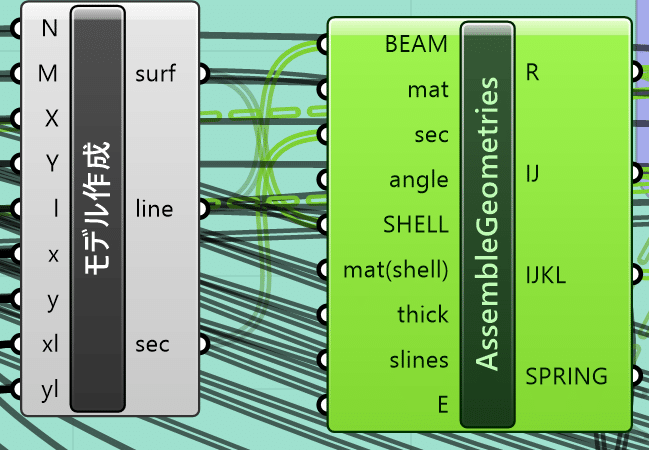
■Assemble Geometries説明（梁・シェル・ばね要素情報を格納し、要素・接点ベクトルへ変換）（R:節点座標ベクトル、IJ:材料・断面の要素節点関係、 IJkl:材料・板厚の要素節点関係）
　OpenSees＞Utility＞Assemble Geometriesから取り出します。下記画像を参考にモデル作成GHPythonコンポーネントのsurf, line, secを、SHELL, BEAM, secに繋ぎます。

画像14

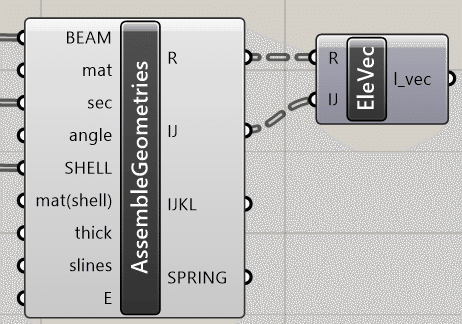
■Ele Vec説明（座標変換マトリクスの計算）
　OpenSees＞Preprocess＞calc Element Axis Vectorから取り出します。Assemble GeometriesからR, IJをつなぎます。

画像15

■柱・梁の種類決定
　柱と梁の種類を選択するためにGHPythonでプログラミングを組みます。
　GHPythonを取り出してください。コンポーネントの左右の数・名前を下記画像になるように変更してください。

画像16

　Pythonのコード中身についてです。コードは以下のように書いてください。＃の後は簡潔な説明を書いており、プログラムに影響はありません。今回は、梁を450 x 200 x 12 x 19のH型鋼、柱を355.6 x 9.0の丸鋼としています。 

S=["H","○"]#H-450x200x12x19, ○-355.6x9.0
P1=[0.45,0.355]#梁せい,外形
P2=[0.2,0.009]#梁幅,鋼管厚
P3=[0.012,0]#ウェブ厚,なし
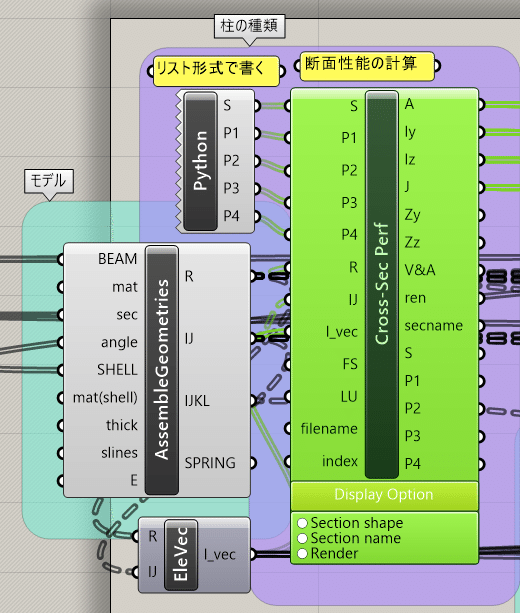
P4=[0.019,0]#フランジ厚,なし

■Calc Section Performance説明 （ 断面性能の計算コンポーネント）
　断面性能の計算コンポーネントを、OpenSees＜Preprocess＜Calc Section Performanceから取り出します。下記画像を参考にこのコンポーネントに繋いでいきます。先程作成した柱・梁種類のGHPythonコンポーネントから、S, P1, P2, P3, P4をつなぎます。Assemble GeometriesからR,IJをつなぎます。Ele Vecからl_vecをつなぎます。以上で断面性能の計算が完了します。

画像17

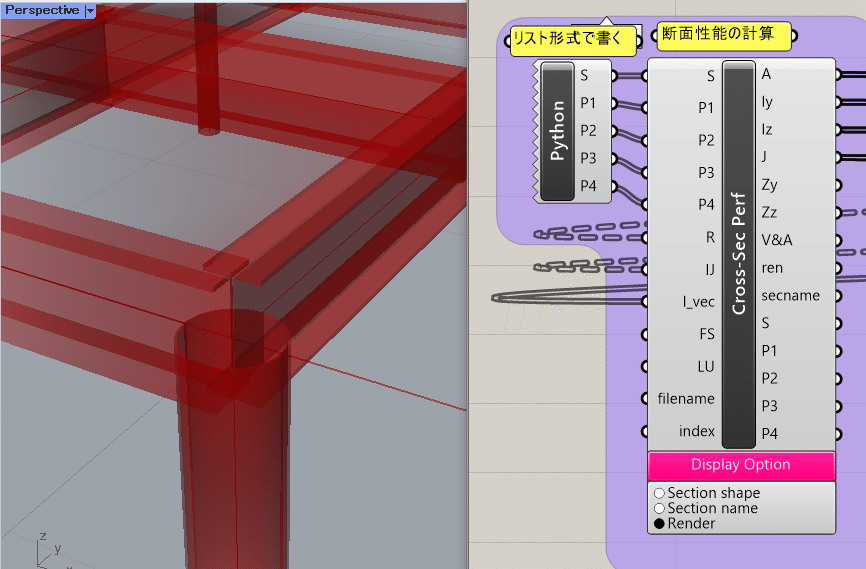
　この断面性能の計算コンポーネントにおいて、「Render」を押すことにより柱や梁の可視化ができ、Ｈ形鋼・〇鋼を確認できます。

画像18

■境界条件作成
　今回の境界条件は、柱脚座標の位置（柱の端部）が固定端となるようにします。境界条件を作成するためにGHPythonでプログラミングを組みます。
　GHPythonを取り出してください。コンポーネントの左右の数・名前を下記画像になるように変更してください。

画像19

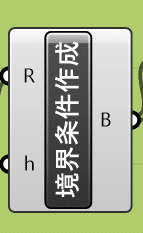
　Pythonのコード中身についてです。コードは以下のように書いてください。 

B=[]
for i in range(len(R)):
   zi=R[i][2]
   if(abs(h+zi)<5e-3):
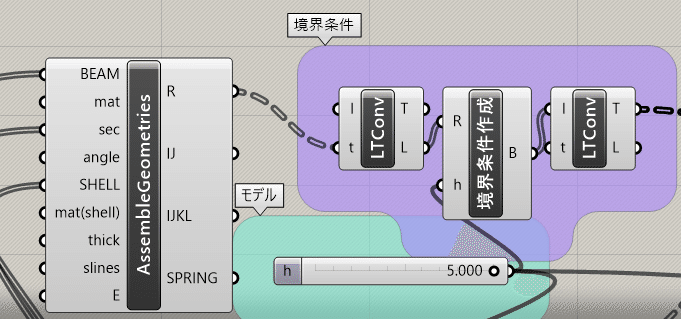
       B.append([i,1,1,1,1,1,1])

　次に、コンポーネントのつなぎ方は下記画像のようになっています。境界条件作成のために、Assemble GeometriesからのR情報が欲しいのですが、Pythonのコード内を見てわかるように、ツリー情報のRをリスト情報に変換する必要があります。そこで、Convert list and tree（リスト・ツリーを相互変換するコンポーネント）を取り出します。Sets＜List＜ Convert list and treeから取り出します。下記画像のように繋げてください。Assemble GeometriesからRをt（ツリー）につなぎ、l（リスト）から境界条件作成GHPythonのＲにつなぎます。
　また、ｈ情報（階高）も欲しいため、下記画像のように繋げてください。モデル作成時に利用したlからつなぐことができます。
　GHPythonで出力される情報はリスト情報なため、解析ができるようにツリー情報に再度変換するように画像のように繋げてください。以上でツリー情報の境界条件を作成できます。

画像20

■モデル作成可視化
　実際に今まで作成したものが正しく反映しているか確認するために、モデルの可視化を行います。確認のためのコンポーネントのため、このコンポーネントがなくても解析や最適化を行うことが可能です。
　モデル可視化のコンポーネントを、OpenSees＜Visualization＜Visual Structural Modelから取り出します。下記画像を参考にこのコンポーネントに繋いでいきます。(荷重説明時に作成する長期面荷重をつなげることで、面荷重も可視化することができます。)Assemble Geometriesから、R, IJをつなぎます。ツリー情報の境界条件のコンポーネントからBoundaryへつなぎます。以上で可視化することができます。

画像21

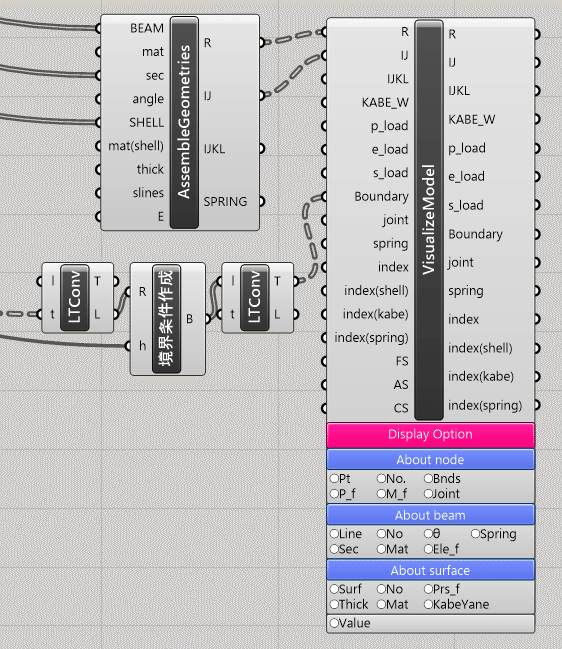
　コンポーネント下部にあるAbout beam<Line, No. 、About node<No. , Bnds等を押すと部材、部材数、接点数、境界条件等を可視化することができます。

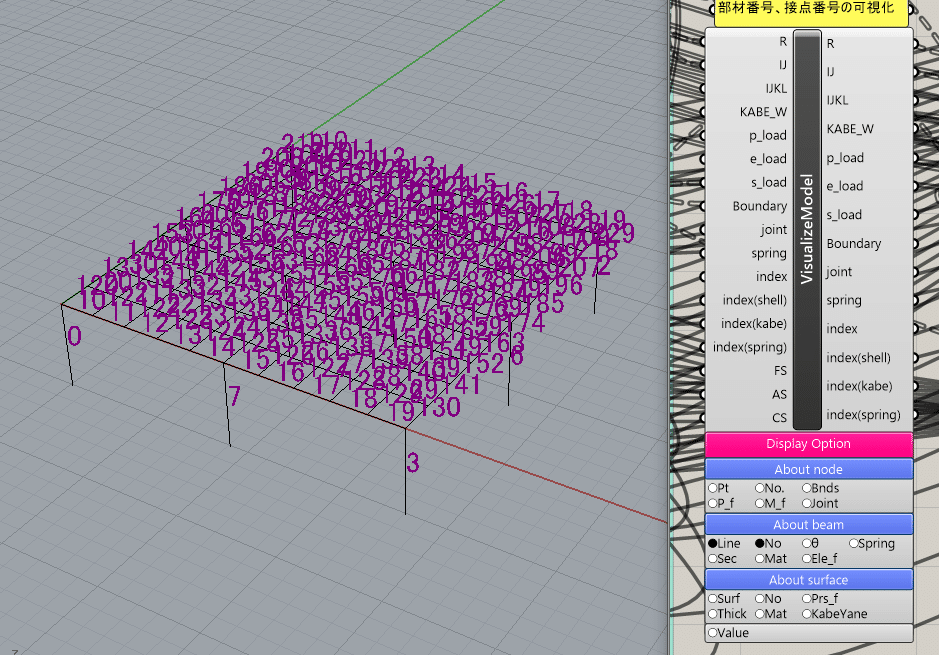
21部材番号

部材番号

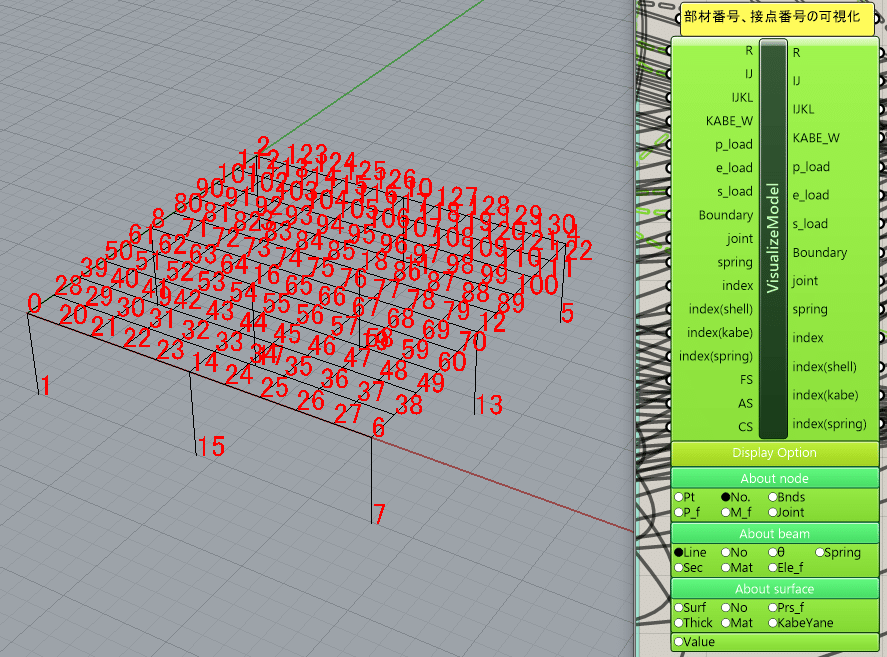
22節点番号

節点番号

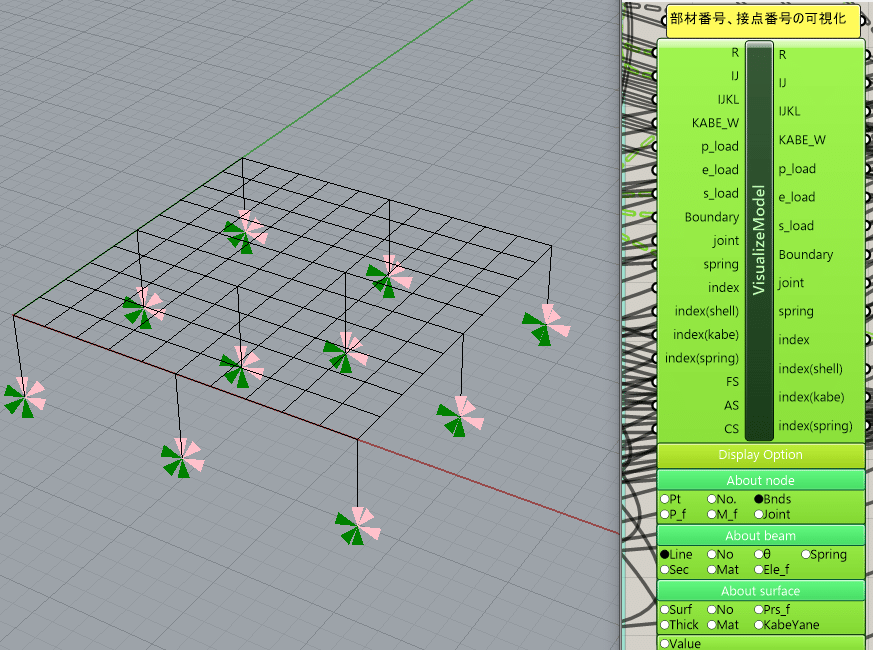
23境界条件

境界条件

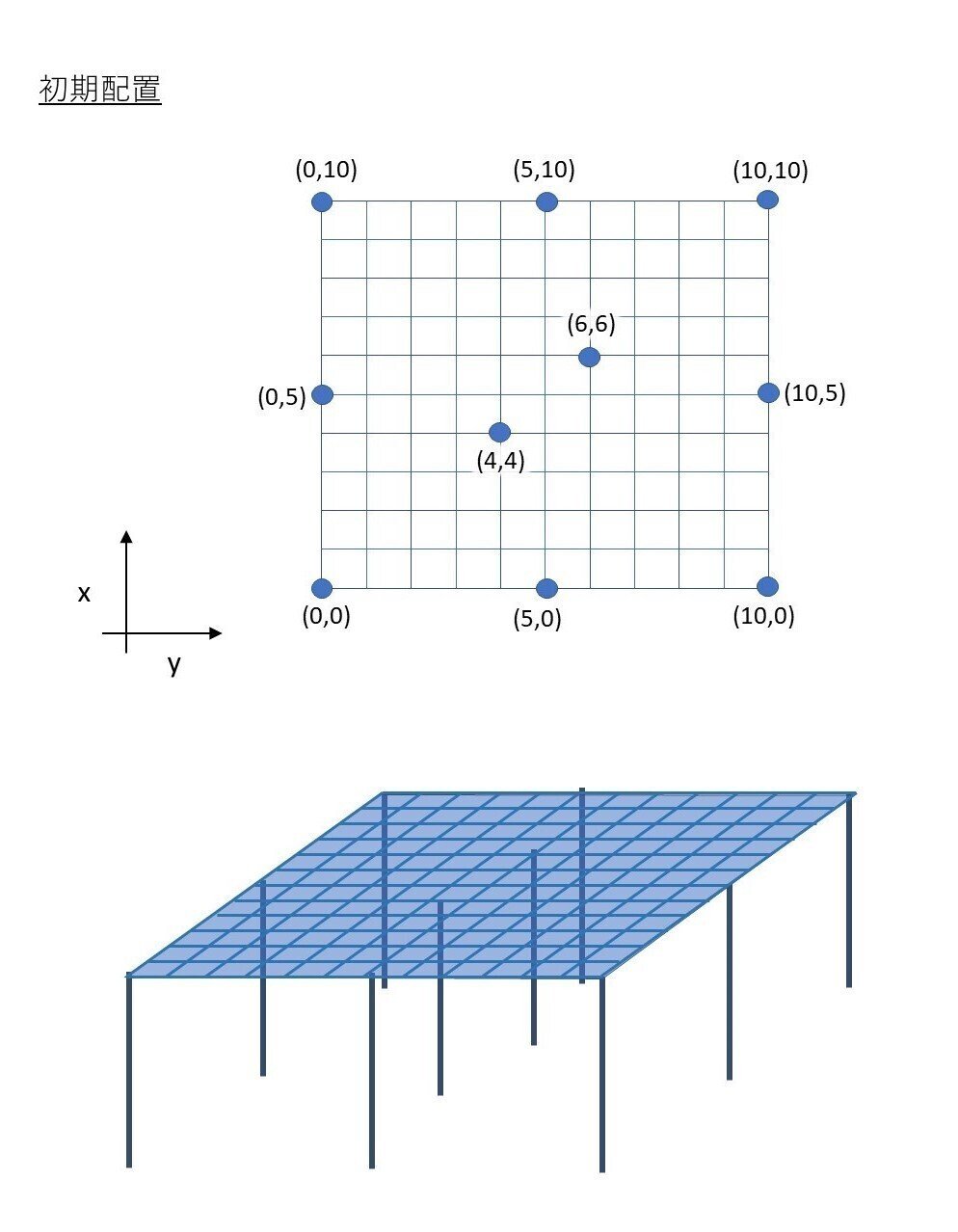
柱初期配置

　以上を初期条件とし、初期位置を設定します。


荷重説明：自重、外力（地震荷重）

　自重と外力についてです。自重は、長期面荷重を柱と梁にかかる自重として設定しています。構造解析上、柱梁情報と長期面荷重情報の総合的な荷重が必要なことに注意してください。外力は、構造解析の短期荷重を取り扱う際に説明します。短期荷重として、今回は地震力をかけます。

■SurfLoads説明（自重・長期面荷重）
柱と梁にかかる自重として２kN/㎡の面荷重をかけます。
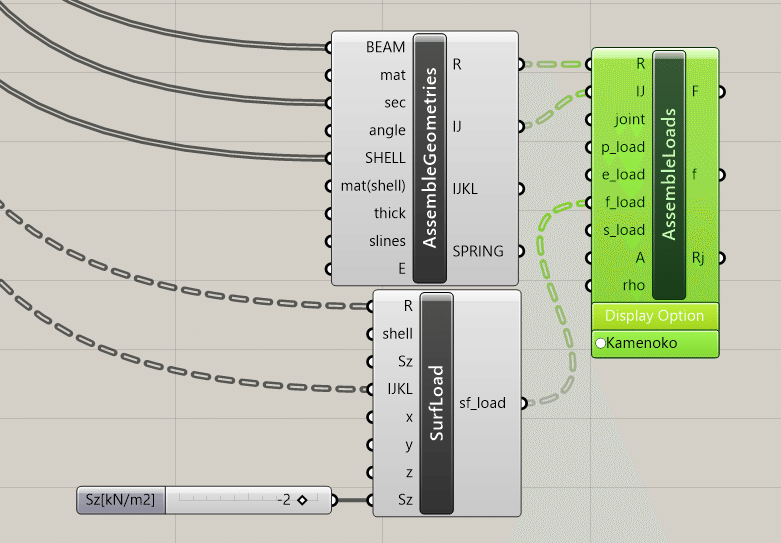
　面荷重コンポーネントを、OpenSees＜Preprocess＜SetSurfLoadsから取り出します。下記画像を参考にこのコンポーネントに繋いでいきます。Assemble GeometriesからR, IJklをつなぎます。Szに面荷重の大きさとして、-2をつなぎます。マイナスを入れることで、Z軸負の方向に荷重がかかっています。以上で面荷重の設定が完了します。

画像26

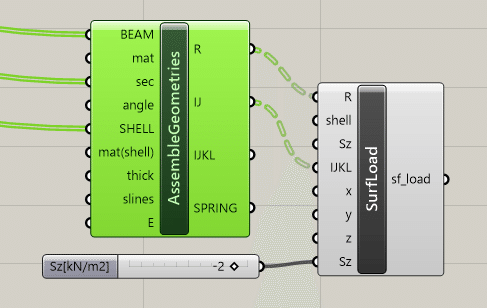
■Assemble Loads説明
(F:節点外力ベクトル,外力曲げモーメント等、ｆ:要素内力ベクトル)
　柱梁情報と長期面荷重情報を格納していきます。構造解析上、総合的な荷重の情報が必要です。
　Assemble Loadsのコンポーネントを、OpenSees＜Preprocess＜Assemble Loadsから取り出します。下記画像を参考にこのコンポーネントに繋いでいきます。Assemble GeometriesからR, IJをつなぎます。SurfLoadsからsf_Loadをf_loadへつなぎます。以上でAssemble Loadsへの格納が完了します。

画像27


★構造解析：長期荷重と短期荷重
（配布データ利用者はここから）

　長期荷重（自重）と短期荷重（地震）による構造解析を行います。長期荷重は自重を利用し、短期荷重は地震力を利用します。地震力については、Ai分布に基づいて作成される地震力生成コンポーネントを利用します。長期荷重構造解析、地震力作成、地震荷重構造解析、解析結果可視化、制約条件作成の順で説明します。

■長期荷重
　長期荷重についての構造解析を行います。
　構造解析のコンポーネントを、OpenSees＜Analysis＜Analysis using OpenSeesから取り出します。下記画像を参考にこのコンポーネントに繋いでいきます。Assemble GeometriesからR, IJをつなぎます。 Assemble LoadsからF, fをつなぎます。ツリー情報の境界条件からBへつなぎます。Ele Vecからl_vecをつなぎます。断面情報コンポーネントからA, Iy, Iz, Jをつなぎます。以上で構造解析のコンポーネントへの格納が完了します。

画像28

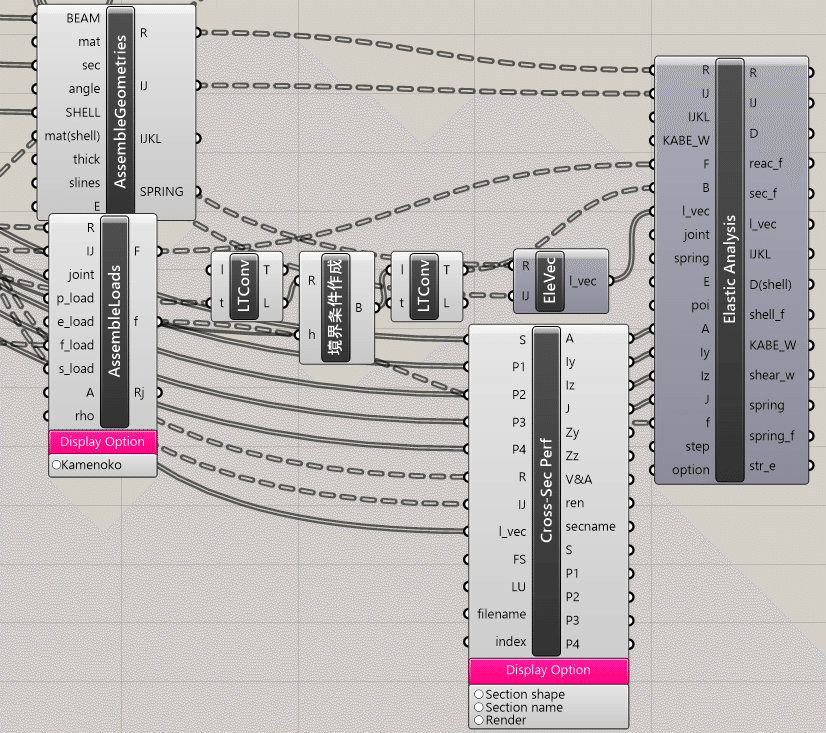
■ SeismicLoads説明
（ Ai分布に基づいて作成される地震力生成コンポーネント）（C0 : せん断力係数、Layer : 各層高さ方向の範囲情報）
　短期荷重の構造解析に必要なAi分布に基づいて作成される地震力を作成していきます。ここでは、Ai分布に基づいて作成される地震力生成コンポーネントについてです。
　SeismicLoadsを、OpenSees＜Preprocess＜ SeismicLoads から取り出します。下記画像を参考にこのコンポーネントに繋いでいきます。Assemble GeometriesからRをつなぎます。 Assemble LoadsからFをつなぎます。 Layerには範囲情報のため、GHPythonで入力します。 GHPythonを取り出してください。コンポーネントの左右の数・名前・コードを下記画像・コードになるように変更してください。 

layer=[
[-0.1,0.1]
]

　Python内ではListになっておりツリー情報のLayerをリスト情報に変換する必要があるため、境界条件作成時と同様にConvert list and tree を使用しツリー情報に変換してからつないでください。今回C0には0.5を入力します。ここでせん断力係数を0.5にした理由は、中程度の地震を想定し安全側に配慮するためです。一般的な中程度の地震に対しては0.2を入力します。以上で SeismicLoads への格納が完了します。これによって作成されたx, y方向地震力（FX, FY）を使用します。

画像29

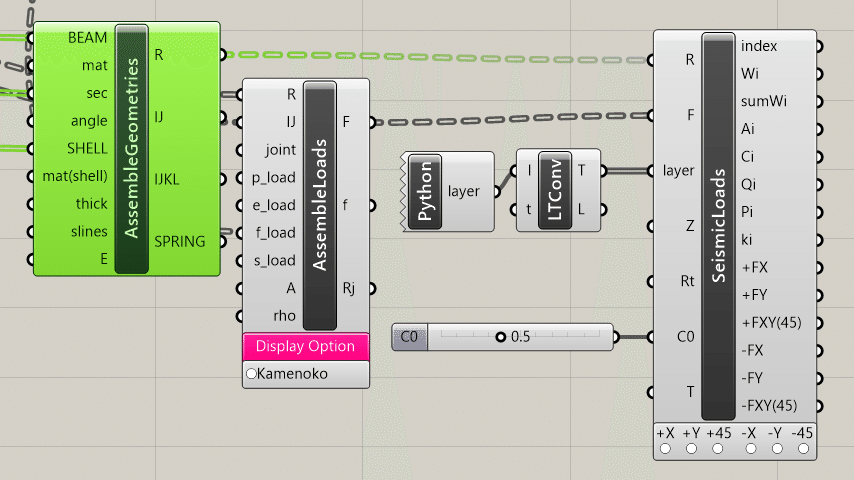
■地震荷重(短期x方向,短期y方向)
　短期荷重についての構造解析を行います。
　構造解析のコンポーネントは、長期荷重時に作成したコンポーネントをコピー＆ペーストすることで時短を行います。理由としては、つながっている情報がFを除いて同じだからです。
　では、下記画像を参考にx, y方向二つ分のコンポーネントをコピー＆ペーストしてください。また、この時にFがAssemble Loadsからつながっているままのコンポーネントがコピーされます。そのため、Fを一度解除する必要があります。（Ctrlキーを押しながら繋ぎなおすことで解除できます。）

画像30

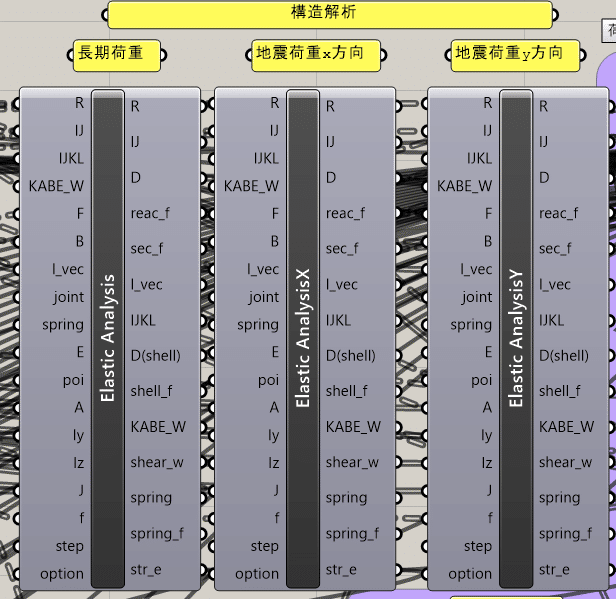
　解除した後、SeismicLoadsから+Fx, +Fyのそれぞれを、x方向y方向の短期荷重解析コンポーネントのFそれぞれにつなぎます。（下記画像は、便宜上F以外の要素を解除しています。構造解析を行うために、長期荷重の構造解析と同様につなぐ必要はあります。）

画像31

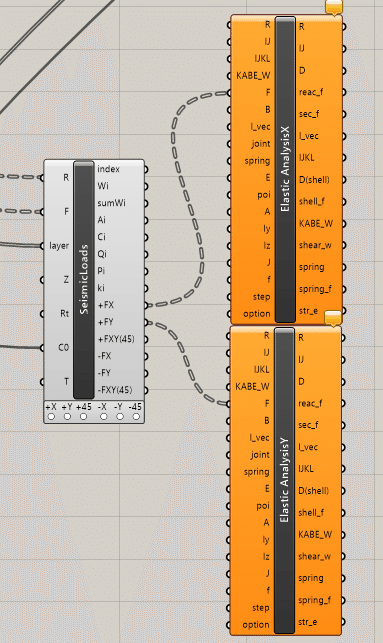
　以上で構造解析のコンポーネントへの格納が完了します。
　改めて注意点としては、Fに格納する情報が長期荷重と違うことです。


■VisSelect説明（構造解析結果をまとめるコンポーネント）
　これまでに作成した構造解析の結果を一つにまとめます。
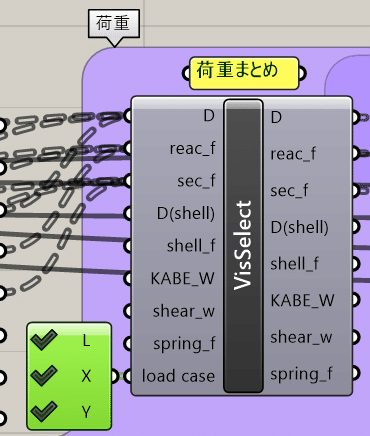
　VisSelectのコンポーネントを、OpenSees＜Visualization＜Visualize Selectionから取り出します。下記画像を参考にこのコンポーネントに繋いでいきます。長期荷重・短期荷重の構造解析コンポーネントそれぞれから、D, reac_f, sec_fの３つずつ計９つをつないでいきます。同じ箇所に複数個つなげる場合はShiftキーを押しながら繋げてください。以上で解析結果のVisSelectへの格納が完了します。

画像32

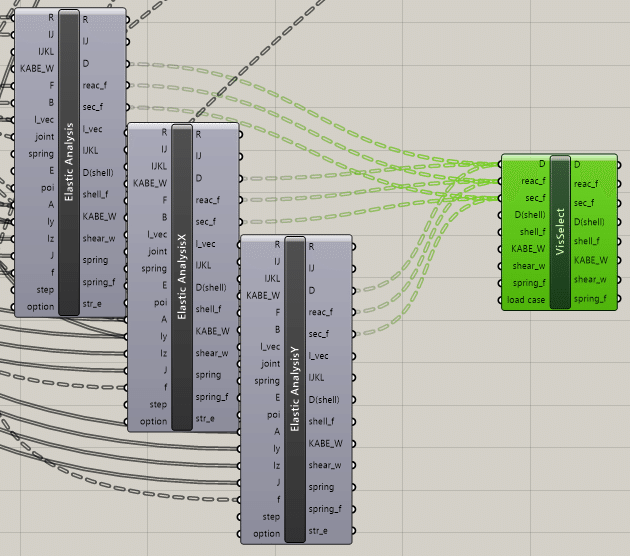
　ここで、格納した荷重情報を切り替えるようなチェックリストを作成します。
　Value Listのコンポーネントを、Params＜Input＜ Value List から取り出します。下記画像を参考にこのコンポーネントに変更を加えます。取り出し初期は画像内左のようにDropdown Listになっているため、コンポーネント上で右クリックを押し、Check Listを選択します。

画像33

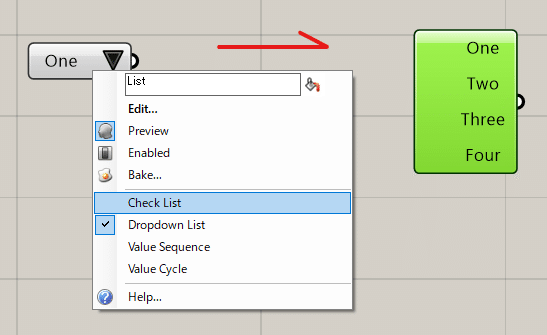
　このままでは切り替えられないため、チェックリストの項目を変更します。コンポーネント上でダブルクリックすることでPythonのように変更することができます。下記画像・コードのように入力してください。以上でチェックリストを作成することができます。

画像34

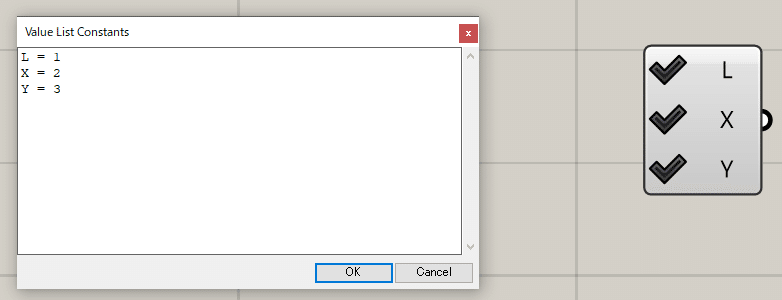
L = 1
X = 2
Y = 3

　次にチェックリストをVisSelectにつなげることで荷重を切り替えることができるようにします。チェックリストをつないでいきます。同じ箇所に複数個つなげる場合はShiftキーを押しながら繋げてください。以上でVisSelectへの格納が完了します。

画像35

■現在の変形を可視化（Visualize Result）
（ D：梁要素の節点変位ベクトル, reac_f：反力ベクトル, sec_f：梁要素の断面力ベクトル）
　実際に構造解析が正しく反映しているか確認するために、変形の可視化を行います。確認のためのコンポーネントのため、このコンポーネントがなくても最適化を行うことが可能です。最適化をスムーズに、メモリや時間に負荷を与えないように行うには、可視化をオフにして最適化を行うことをお勧めします。
　モデル可視化のコンポーネントを、OpenSees＜Visualization＜Visualize Analysis Resultから取り出します。下記画像を参考にこのコンポーネントに繋いでいきます。Assemble Geometriesから、R, IJをつなぎます。Vis Select からD, reac_f, sec_fをつなぎます。Ele Vecからl_vecをつなぎます。また、変形倍率を大きくすることで変形を見やすくするように、DSに100をつなぎます。DisplaySiseを変更することで変形倍率を変更できます。以上で変形を可視化することができます。

画像36


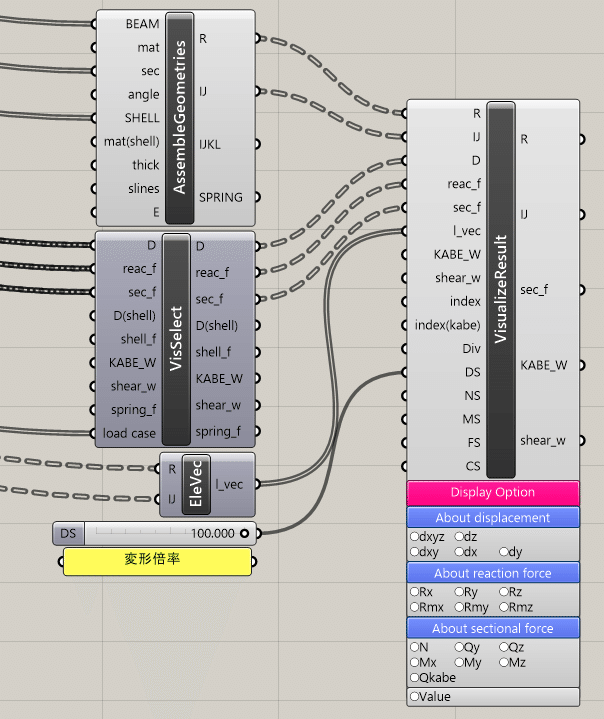
　コンポーネント下部にあるAbout displacement<dxyz, dz等を押すと全体の変形やZ軸だけの変形などを可視化することができます。また、VisSelectで紹介した荷重の切り替えを行うことで、荷重のかけ方による変形の比較することができます。

以下、視覚化の例

画像37

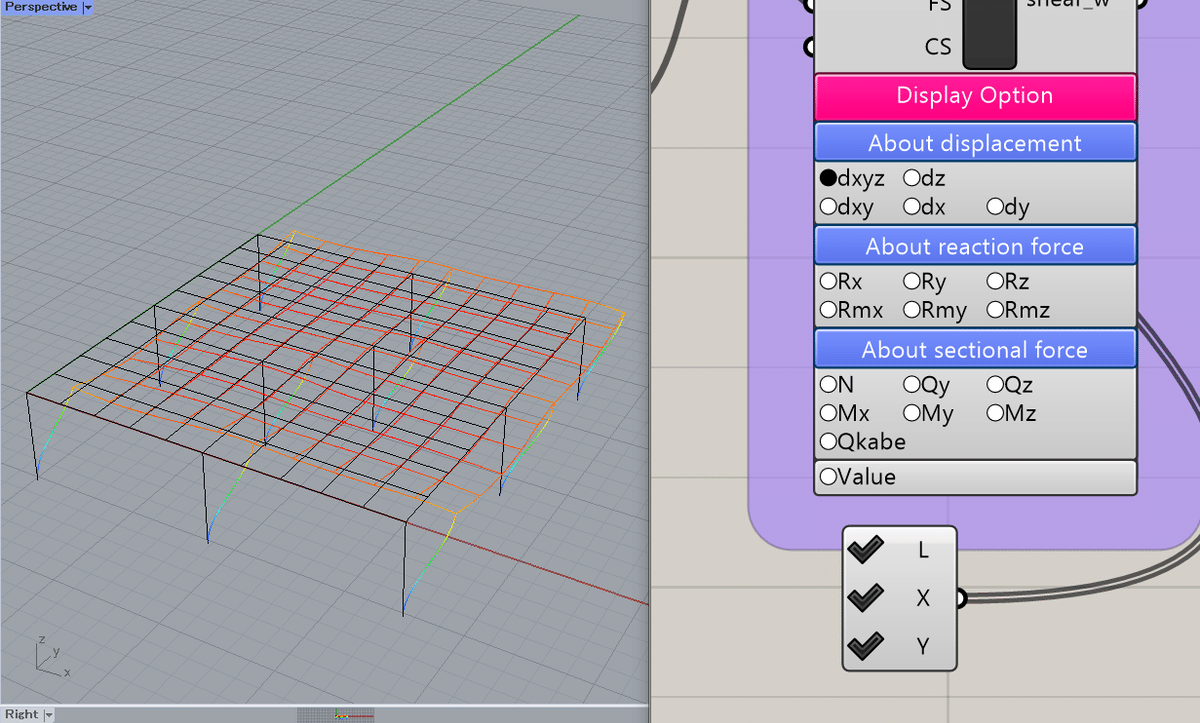
x, y, z方向の総ひずみ（長期,短期選択時）

画像38

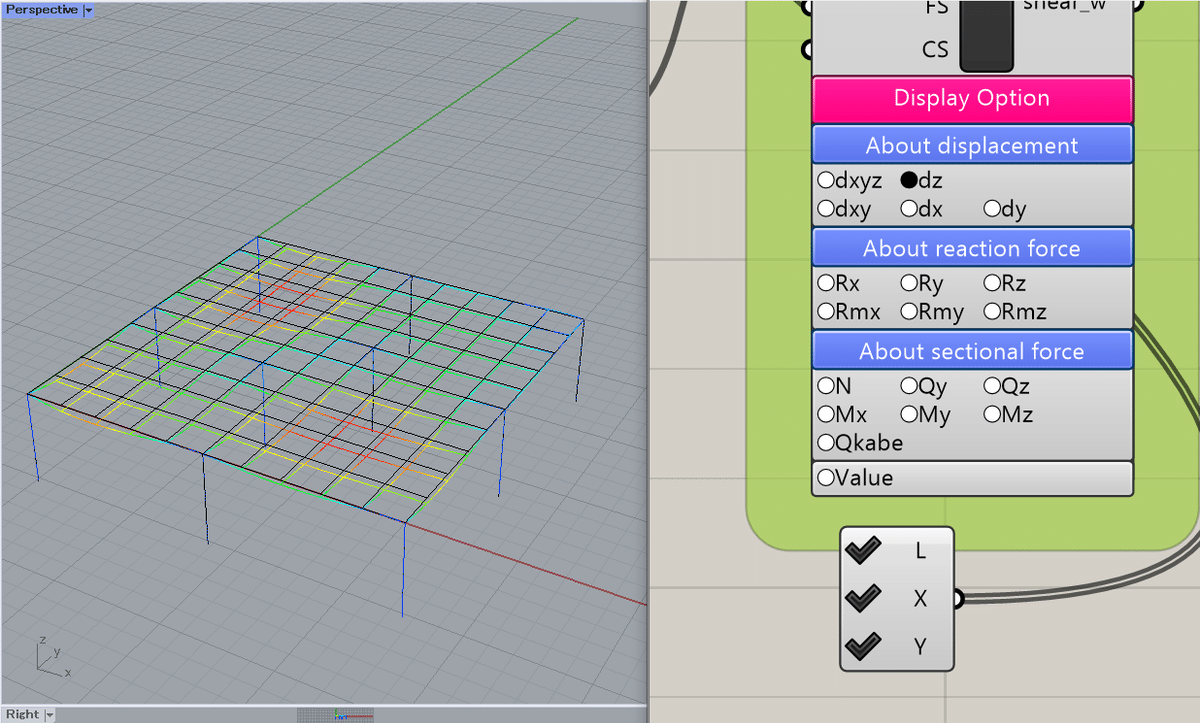
z方向ひずみ（長期,短期選択時）

画像39

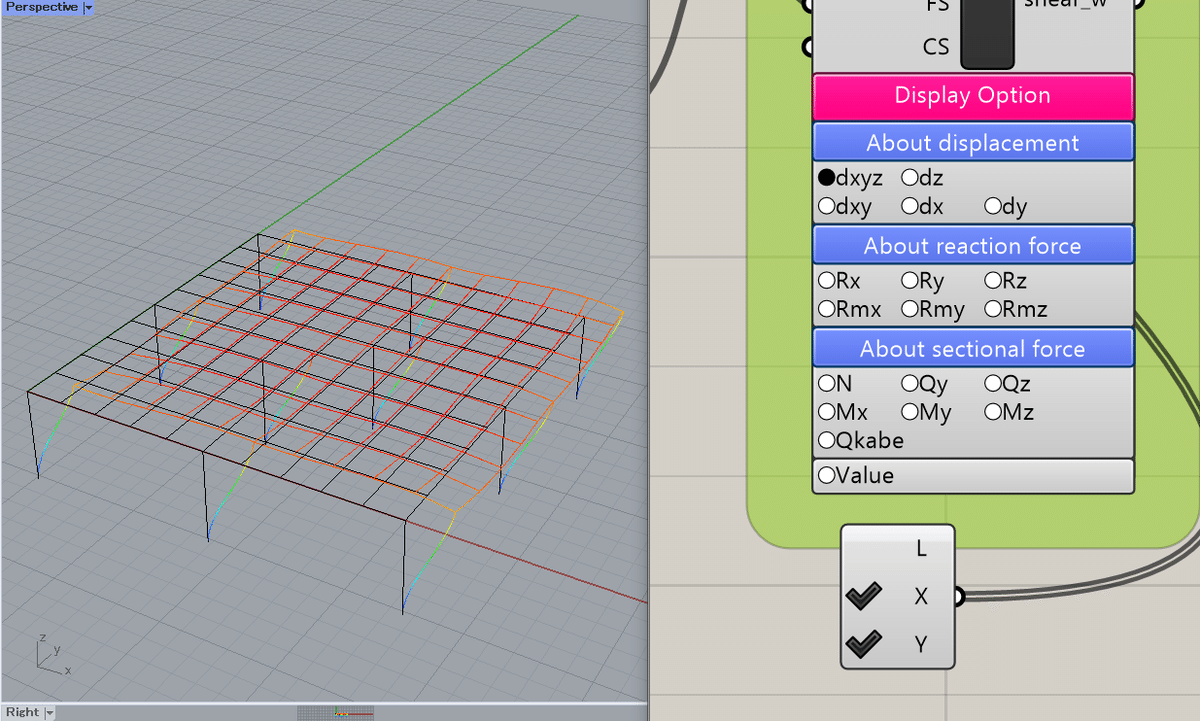
x, y, z方向の総ひずみ（短期選択時）

画像40

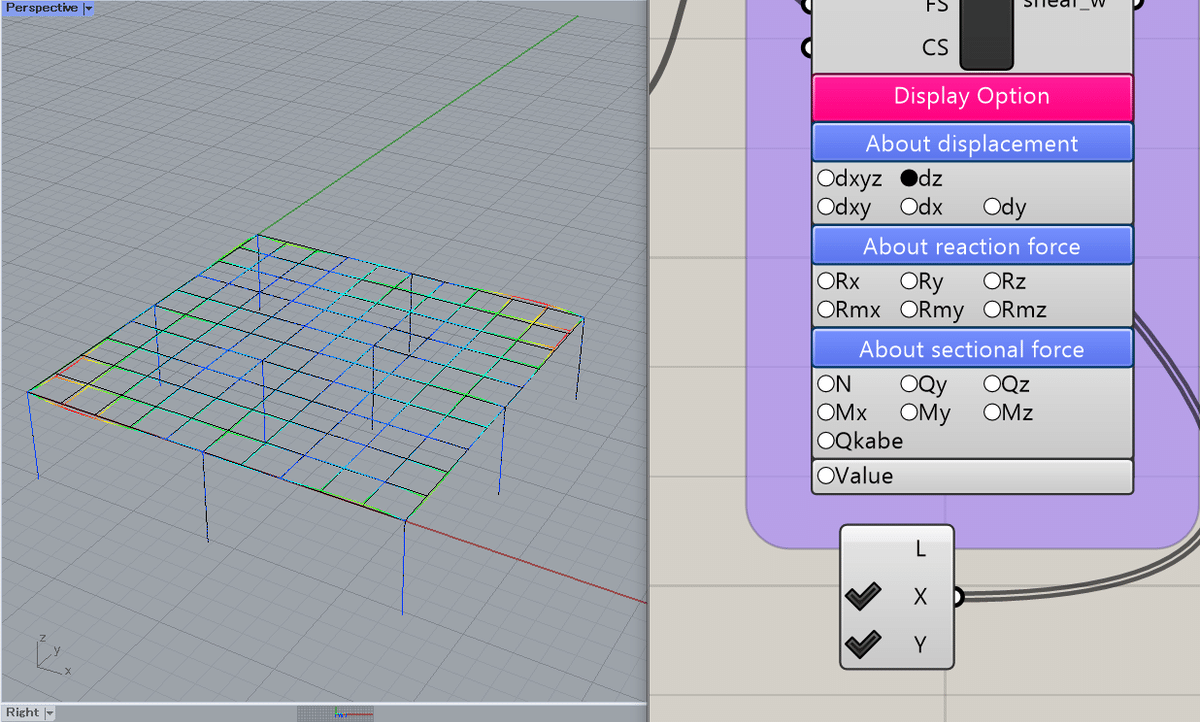
z方向ひずみ（短期選択時）

■GHPythonで制約をかけていく
(str_eL :長期荷重時ひずみエネルギー , str_eX : x方向時ひずみエネルギー, str_eY : y方向時ひずみエネルギー, x : 柱頭のx座標, y : 柱頭のy座標)
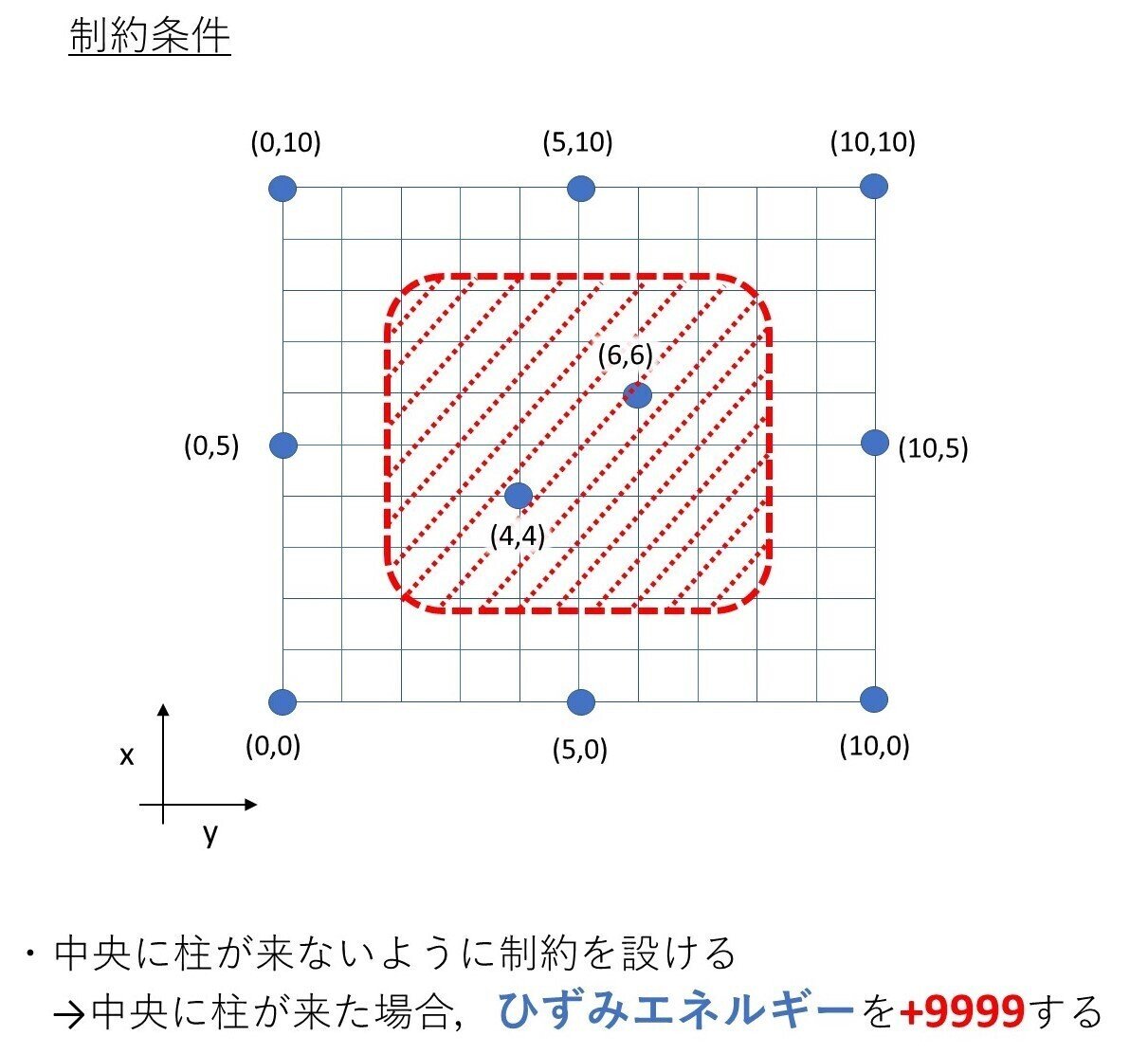
　今回の目的関数であるひずみエネルギーをGHPythonを用いて設定していきます。長期荷重時、x, y方向地震荷重時のひずみエネルギーとペナルティの合計を目的関数にしています。また、ひずみエネルギーを設定していくにあたり、ある条件の柱配置を行わないようにするという制約をGHPythonの中身でプログラムします。今回の制約条件は、20m×20mという広い空間のなかで、柱頭座標が正方形平面中心より12m×12m空間上座標に配置されないという制約条件をプログラムします。
　初めにGHPythonを取り出します。コンポーネントの左右の数・名前を下記画像になるように変更してください。

画像41

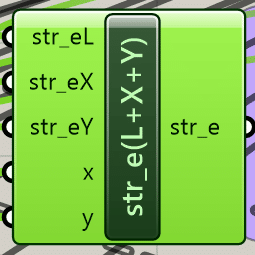
　Pythonのコード中身についてです。コードは以下のように書いてください。

import ghpythonlib.components as gh

n=len(x)
penalty=0.0
for i in range(n):
   if x[i]==3 or x[i]==4 or x[i]==5 or x[i]==6 or x[i]==7:
       if y[i]==3 or y[i]==4 or y[i]==5 or y[i]==6 or y[i]==7:
           penalty+=9999

str_e=str_eL+str_eX+str_eY+penalty

　6行目, 7行目のプログラムが制約条件の内容です。柱頭座標のx, yそれぞれが3-7に配置されないような制約条件になっています。ペナルティの大きさは自由ですが、最適化時にペナルティを大きくすることで選択されづらくすることが目的ですので、なるべく大きくすることを推奨します。

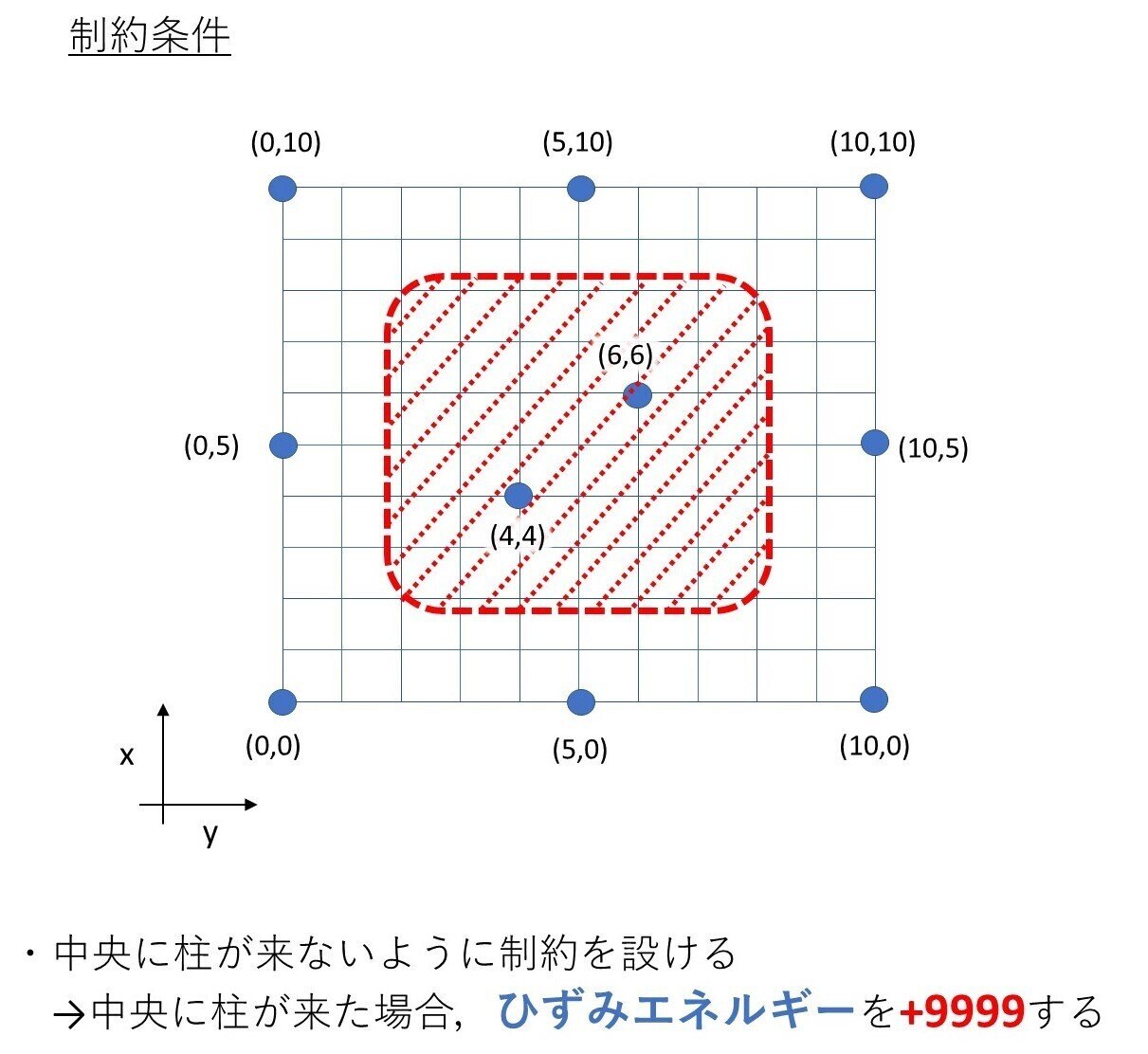
制約条件2

　今回の制約条件を設定する目的は、正方形平面中央部に大空間を確保することです。
　空間作成上の注意点として、ここでは柱頭座標しか制約条件に入れていないため、柱脚座標がx, y方向それぞれに±1される斜め柱が選択された時の空間の広がりに気を付けてください。その他注意点として、制約条件を設定し柱配置を行うことを目的としているため、建築物としての合理性等は別途確認する必要があります。
　次に、コンポーネントのつなぎ方です。下記画像を参考につなぎます。（下記画像は、便宜上、構造解析コンポーネントの左部分を解除しています。いままでつなげてきたものを使用する必要があります。）長期荷重時、x, y方向地震荷重時のひずみエネルギーを構造解析コンポーネントからひずみエネルギーを表すstr_eにそれぞれつなぎます。柱頭の座標 のスライダーから、x, yにつなぎます。x座標からxに、y座標からyにつなげることに注意してください。

画像44

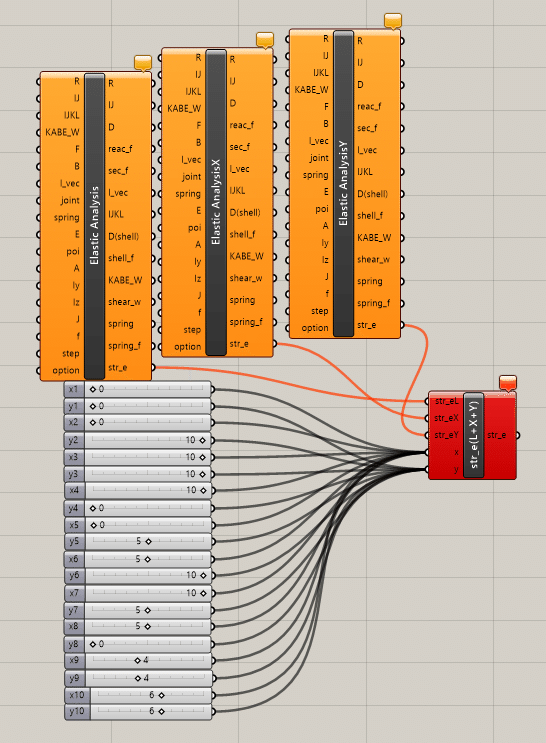
　Panelを付けることで、現在のひずみエネルギーの値を確認することができます。下記画像では、初期位置の状態、つまり制約条件にてPenaltyがかかる状態ですので、ひずみエネルギーの表す値が大きくなっています。

画像45


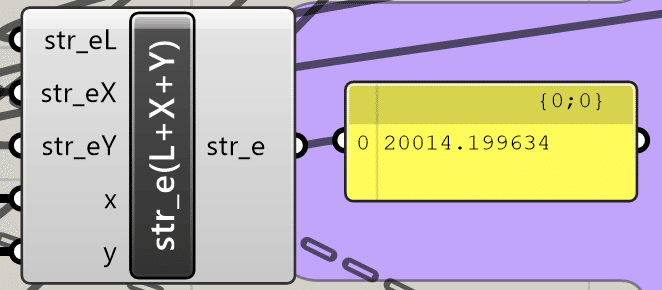
最適化説明

■解析開始
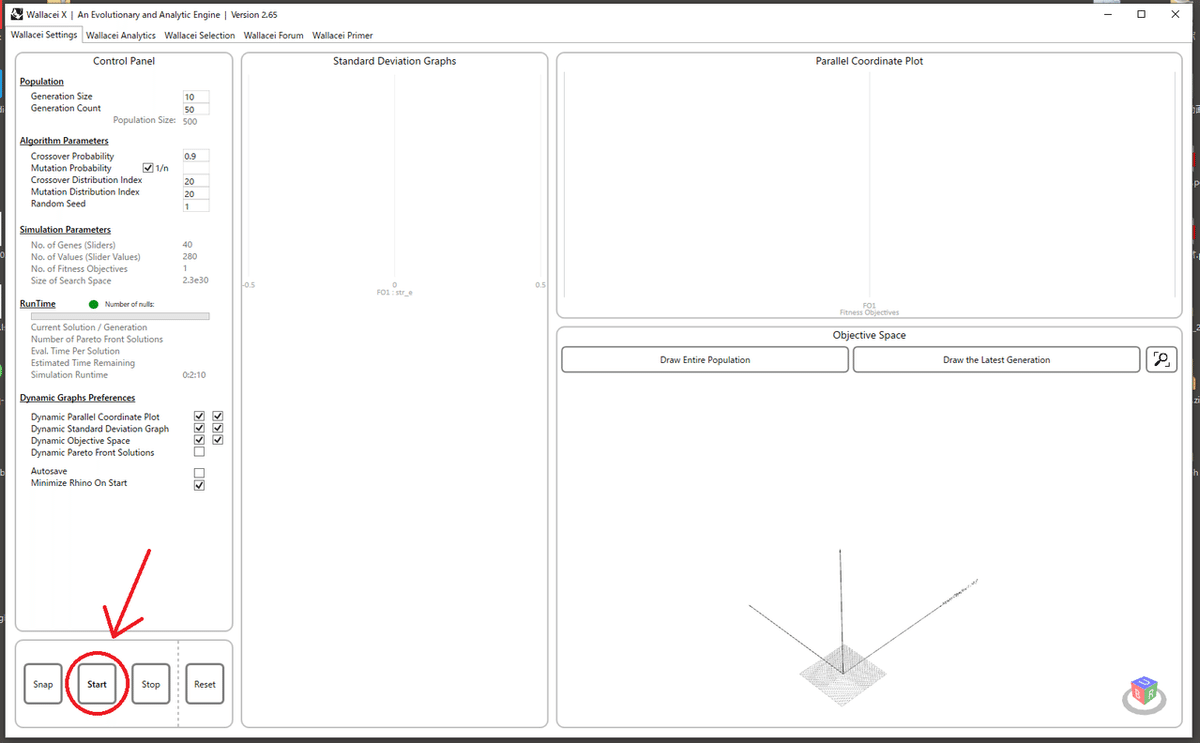
　柱の座標を設計変数、ひずみエネルギーを目的関数とする最適化をしていきます。Wallaceiをダブルクリックして開き、startを押して解析を始めます。

画像47

画像48

-解析終了後-

■最適解の表示
　最適化を回し終わった後は最適化の最後の柱配置が表示されているので、目的解であるひずみエネルギーの一番小さい最適解を表示していきます。
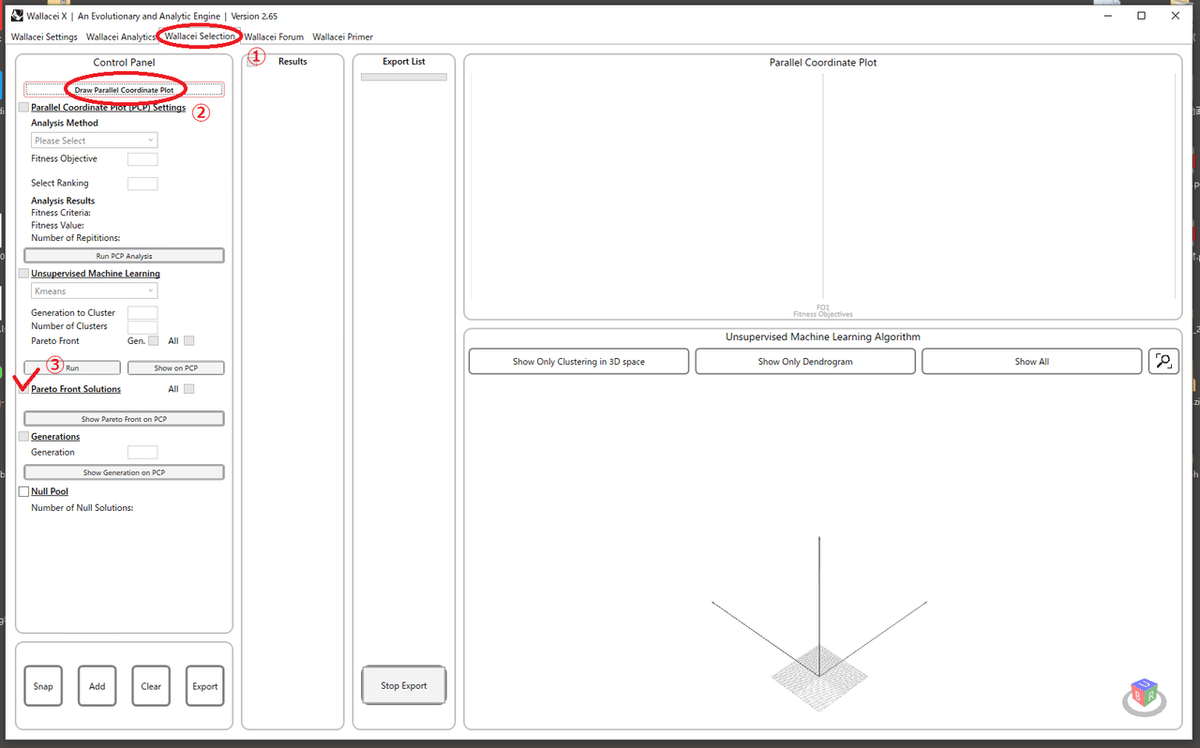
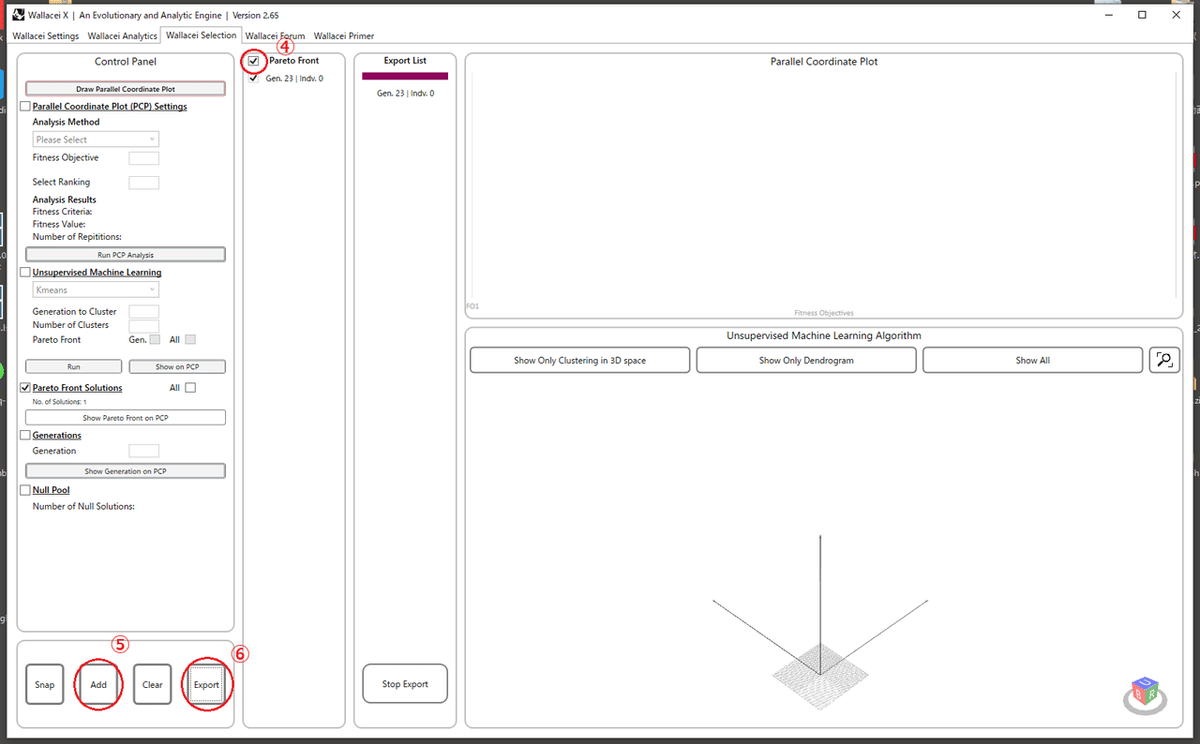
　Wallaceiを開き、 Wallacei Selection→Draw Paralllel Condinate Plot→Pareto Front Solutionsを押し、左から2つ目のPereto Frontにチェックを付け、左下のAdd→Exportで最適化を表示することができます。
　注意点として、Phenotypeにsurfとlineをつないでいないと、この機能が使えないので注意してください。

画像49

画像50

■解析結果可視化
　先ほど使ったVisualize Resultで解析結果を見ることができます。 
　初期配置と最適化後の比較をしていきます。

柱配置

画像52

画像53

画像54

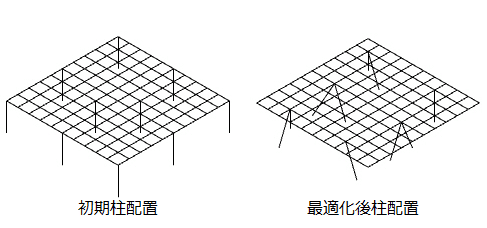
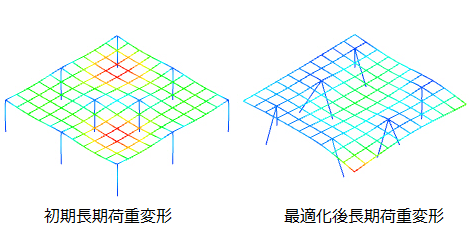
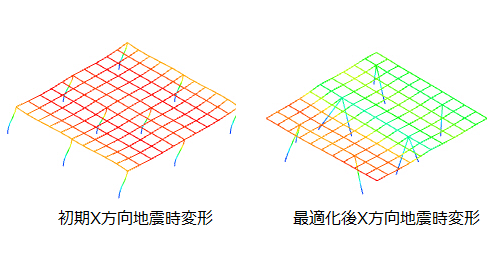
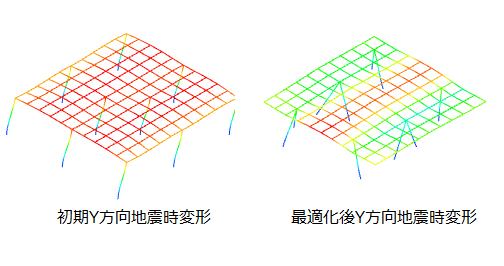
　最適化後は初期配置と比較して、長期荷重のみの時もX方向地震時、Y方向地震時の時も変形が小さくなっていることが分かります。

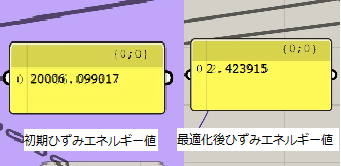
ひずみエネルギー

　初期配置では中心付近に柱が置いてあるのでひずみエネルギーが大きくなっていますが、最適化後はひずみエネルギーも小さくなっています。


CSV出力説明

■CSVに出力
　まとめる時などに使用する結果を出力するcsvファイルを作ります。
　まずは情報を集めるためのGHPythonを作成します。Math＜Script＜GH Pythonのコンポーネントを使用します。 Python内に、nを柱本数、hを階高、XをX方向の梁の長さ、YをY方向の梁の長さ、nxをX方向の接点数、 nyをY方向の接点数として、下記のようにコードを入力することでファイル名を設定できるようにします。

filename=str(n)+"-"+str(h)+"m-"+str(X)+"mx"+str(Y)+"m_"+str(nx)+"x"+str(ny)+".csv"

　出力するものとして、Python内に、xyを柱頭の座標、xiyiを柱脚の座標、str_eに長期荷重時・X方向地震時・Y方向地震時のそれぞれのひずみエネルギーとして、下記のようにコードを入力します。
　注意点として、str_eは座標に比べて入力するものの数が少ないので、空欄に0を入力するようにして、数をそろえます。

L=[]

L.append(xy)
L.append(xiyi)
L.append([str_e[0],str_e[1],str_e[2],0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0])

 　集めた情報を基にCSVファイルとして出力します。Open Sees<Utility<TREEorLISTtoCSVのコンポーネントを使用します。 Treeに先ほどの出力したいものをつなぎ、outputfilenameに作成したfilenameのPythonをつなぎます。Directoryを右クリックし、Set Textに出力先の場所のURLを入力します。 Exportを押すと、設定した出力先にcsvファイルが作成されています。

画像56

画像57

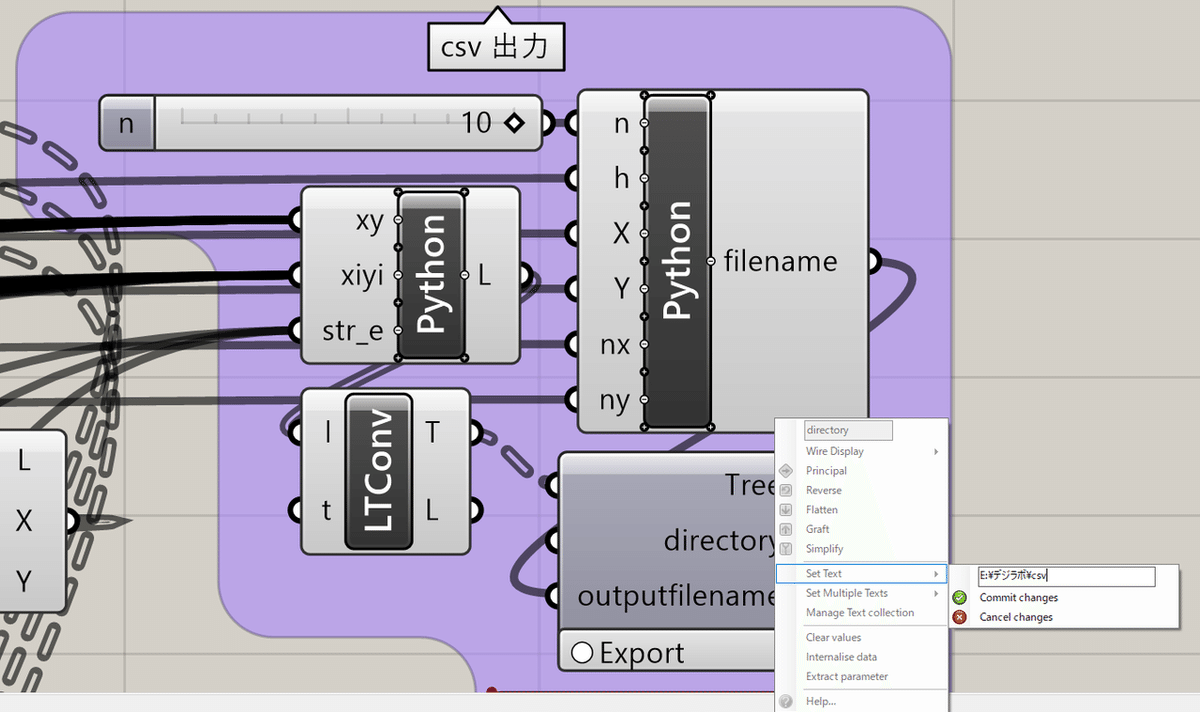
-------------------説明終了--------------------

まとめ

・モデル作成から構造解析、Wallaceiによる斜め柱を考慮した柱配置最適化を行った。
・今回はひずみエネルギーのみを目的関数とした最適化を行った。
・今後の展望として、目的関数を増やすことを検討することや、今回考慮できていない要素（地震力生成時の係数や階層を増やすことなど）がどのように目的関数に影響を及ぼす必要があるかなどの検討が必要である。また、実際に構造上安全な建物なのかなどの検討が必要である。


おわりに

　大変お疲れ様でした。GreatJob！！以上， Wallaceiを使ってひずみエネルギーを最小化する斜め柱を考慮した柱配置最適化の紹介でした。動画で取り扱っていない部分をできる限り詳しく説明させていただきました。拙い文をお読みいただきありがとうございました。今後も応援のほどよろしくお願いいたします。


今回参考にしたもの

・ ”OpenSees for Grasshopper wiki”

・”建築学生が学ぶ「構造力学」より”地震力の算定方法と、簡単にわかるZ、Rt、Ai、Coの意味”


いいなと思ったら応援しよう！